title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Roman to Integer - Jesse | roman-to-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def romanToInt(self, s: str) -> int:\n roman = { "I": 1, "V": 5, "X": 10, "L": 50, "C": 100, "D": 500, "M": 1000}\n\n res = 0\n\n for i in range(len(s)):\n if i + 1 < len(s) and roman[s[i]] < roman[s[i + 1]]:\n res -= roman[s[i]]\n else:\n res += roman[s[i]]\n return res\n``` | 5 | Roman numerals are represented by seven different symbols: `I`, `V`, `X`, `L`, `C`, `D` and `M`.
**Symbol** **Value**
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, `2` is written as `II` in Roman numeral, just two ones added together. `12` is written as `XII`, which is simply `X + II`. The number `27` is written as `XXVII`, which is `XX + V + II`.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not `IIII`. Instead, the number four is written as `IV`. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as `IX`. There are six instances where subtraction is used:
* `I` can be placed before `V` (5) and `X` (10) to make 4 and 9.
* `X` can be placed before `L` (50) and `C` (100) to make 40 and 90.
* `C` can be placed before `D` (500) and `M` (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
**Example 1:**
**Input:** s = "III "
**Output:** 3
**Explanation:** III = 3.
**Example 2:**
**Input:** s = "LVIII "
**Output:** 58
**Explanation:** L = 50, V= 5, III = 3.
**Example 3:**
**Input:** s = "MCMXCIV "
**Output:** 1994
**Explanation:** M = 1000, CM = 900, XC = 90 and IV = 4.
**Constraints:**
* `1 <= s.length <= 15`
* `s` contains only the characters `('I', 'V', 'X', 'L', 'C', 'D', 'M')`.
* It is **guaranteed** that `s` is a valid roman numeral in the range `[1, 3999]`. | Problem is simpler to solve by working the string from back to front and using a map. |
test | roman-to-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def romanToInt(self, s: str) -> int:\n roman={"I":1,"V":5,"X":10,"L":50,"C":100,"D":500,"M":1000}\n number=0\n for i in range(len(s)-1):\n if roman[s[i]] < roman[s[(i+1)]]:\n number-=roman[s[i]]\n else:\n number+=roman[s[i]]\n return number+roman[s[-1]]\n``` | 0 | Roman numerals are represented by seven different symbols: `I`, `V`, `X`, `L`, `C`, `D` and `M`.
**Symbol** **Value**
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, `2` is written as `II` in Roman numeral, just two ones added together. `12` is written as `XII`, which is simply `X + II`. The number `27` is written as `XXVII`, which is `XX + V + II`.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not `IIII`. Instead, the number four is written as `IV`. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as `IX`. There are six instances where subtraction is used:
* `I` can be placed before `V` (5) and `X` (10) to make 4 and 9.
* `X` can be placed before `L` (50) and `C` (100) to make 40 and 90.
* `C` can be placed before `D` (500) and `M` (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
**Example 1:**
**Input:** s = "III "
**Output:** 3
**Explanation:** III = 3.
**Example 2:**
**Input:** s = "LVIII "
**Output:** 58
**Explanation:** L = 50, V= 5, III = 3.
**Example 3:**
**Input:** s = "MCMXCIV "
**Output:** 1994
**Explanation:** M = 1000, CM = 900, XC = 90 and IV = 4.
**Constraints:**
* `1 <= s.length <= 15`
* `s` contains only the characters `('I', 'V', 'X', 'L', 'C', 'D', 'M')`.
* It is **guaranteed** that `s` is a valid roman numeral in the range `[1, 3999]`. | Problem is simpler to solve by working the string from back to front and using a map. |
Very Simple Python Solution | roman-to-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe essentially start scanning adding all of the corresponding values for each character regardless of order. (e.g. "IX" is 11 not 9) Then, we check the order of the elements, and if we find that the order is reversed (i.e. "IX"), we make the necessary adjustment (e.g. for "IX," we subtract 2)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) Introduce the total sum variable, and the dictionary containing the corresponding number values for each Roman letter\n2) We add all of the corresponding number values together regardless of order of elements\n3) We check if certain ordered pairs are in the Roman number and make the adjustments if necessary\n\n\n# Code\n```\nclass Solution:\n def romanToInt(self, s: str) -> int:\n total = 0\n theDict = {"I": 1, "V": 5, "X": 10, "L": 50, "C": 100, "D": 500, "M": 1000}\n\n for i in s:\n total += theDict[i]\n\n if "IV" in s:\n total -= 2\n if "IX" in s:\n total -= 2\n if "XL" in s:\n total -= 20\n if "XC" in s:\n total -= 20\n if "CD" in s:\n total -= 200\n if "CM" in s:\n total -= 200\n\n \n return total\n``` | 51 | Roman numerals are represented by seven different symbols: `I`, `V`, `X`, `L`, `C`, `D` and `M`.
**Symbol** **Value**
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, `2` is written as `II` in Roman numeral, just two ones added together. `12` is written as `XII`, which is simply `X + II`. The number `27` is written as `XXVII`, which is `XX + V + II`.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not `IIII`. Instead, the number four is written as `IV`. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as `IX`. There are six instances where subtraction is used:
* `I` can be placed before `V` (5) and `X` (10) to make 4 and 9.
* `X` can be placed before `L` (50) and `C` (100) to make 40 and 90.
* `C` can be placed before `D` (500) and `M` (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
**Example 1:**
**Input:** s = "III "
**Output:** 3
**Explanation:** III = 3.
**Example 2:**
**Input:** s = "LVIII "
**Output:** 58
**Explanation:** L = 50, V= 5, III = 3.
**Example 3:**
**Input:** s = "MCMXCIV "
**Output:** 1994
**Explanation:** M = 1000, CM = 900, XC = 90 and IV = 4.
**Constraints:**
* `1 <= s.length <= 15`
* `s` contains only the characters `('I', 'V', 'X', 'L', 'C', 'D', 'M')`.
* It is **guaranteed** that `s` is a valid roman numeral in the range `[1, 3999]`. | Problem is simpler to solve by working the string from back to front and using a map. |
Easiest Beginner Friendly Sol || HashMap || C ++, Java, Python | roman-to-integer | 1 | 1 | # Intuition of this Problem:\nThe given code is implementing the conversion of a Roman numeral string into an integer. It uses an unordered map to store the mapping between Roman numerals and their corresponding integer values. The algorithm takes advantage of the fact that in a valid Roman numeral string, the larger numeral always appears before the smaller numeral if the smaller numeral is subtracted from the larger one. Thus, it starts with the last character in the string and adds the corresponding value to the integer variable. Then, it iterates through the remaining characters from right to left and checks whether the current numeral is greater than or equal to the previous numeral. If it is greater, then it adds the corresponding value to the integer variable, otherwise, it subtracts the corresponding value from the integer variable.\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Create an unordered map and store the mapping between Roman numerals and their corresponding integer values.\n2. Reverse the input Roman numeral string.\n3. Initialize an integer variable to 0.\n4. Add the integer value corresponding to the last character in the string to the integer variable.\n5. Iterate through the remaining characters from right to left.\n6. Check whether the integer value corresponding to the current character is greater than or equal to the integer value corresponding to the previous character.\n7. If it is greater, add the integer value to the integer variable.\n8. If it is smaller, subtract the integer value from the integer variable.\n9. Return the final integer variable.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int romanToInt(string s) {\n unordered_map<char, int> storeKeyValue;\n storeKeyValue[\'I\'] = 1;\n storeKeyValue[\'V\'] = 5;\n storeKeyValue[\'X\'] = 10;\n storeKeyValue[\'L\'] = 50;\n storeKeyValue[\'C\'] = 100;\n storeKeyValue[\'D\'] = 500;\n storeKeyValue[\'M\'] = 1000;\n reverse(s.begin(), s.end());\n int integer = 0;\n integer += storeKeyValue[s[0]];\n for (int i = 1; i < s.length(); i++) {\n if(storeKeyValue[s[i]] >= storeKeyValue[s[i-1]])\n integer += storeKeyValue[s[i]];\n else\n integer -= storeKeyValue[s[i]];\n }\n return integer;\n }\n};\n```\n```Java []\nclass Solution {\n public int romanToInt(String s) {\n HashMap<Character, Integer> storeKeyValue = new HashMap<>();\n storeKeyValue.put(\'I\', 1);\n storeKeyValue.put(\'V\', 5);\n storeKeyValue.put(\'X\', 10);\n storeKeyValue.put(\'L\', 50);\n storeKeyValue.put(\'C\', 100);\n storeKeyValue.put(\'D\', 500);\n storeKeyValue.put(\'M\', 1000);\n int integer = 0;\n integer += storeKeyValue.get(s.charAt(0));\n for (int i = 1; i < s.length(); i++) {\n if(storeKeyValue.get(s.charAt(i)) >= storeKeyValue.get(s.charAt(i-1)))\n integer += storeKeyValue.get(s.charAt(i));\n else\n integer -= storeKeyValue.get(s.charAt(i));\n }\n return integer;\n }\n}\n\n```\n```Python []\nclass Solution:\n def romanToInt(self, s: str) -> int:\n storeKeyValue = {}\n storeKeyValue[\'I\'] = 1\n storeKeyValue[\'V\'] = 5\n storeKeyValue[\'X\'] = 10\n storeKeyValue[\'L\'] = 50\n storeKeyValue[\'C\'] = 100\n storeKeyValue[\'D\'] = 500\n storeKeyValue[\'M\'] = 1000\n s = s[::-1]\n integer = 0\n integer += storeKeyValue[s[0]]\n for i in range(1, len(s)):\n if storeKeyValue[s[i]] >= storeKeyValue[s[i-1]]:\n integer += storeKeyValue[s[i]]\n else:\n integer -= storeKeyValue[s[i]]\n return integer\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(s.length()) = O(15) = O(1)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(7) = O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 49 | Roman numerals are represented by seven different symbols: `I`, `V`, `X`, `L`, `C`, `D` and `M`.
**Symbol** **Value**
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, `2` is written as `II` in Roman numeral, just two ones added together. `12` is written as `XII`, which is simply `X + II`. The number `27` is written as `XXVII`, which is `XX + V + II`.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not `IIII`. Instead, the number four is written as `IV`. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as `IX`. There are six instances where subtraction is used:
* `I` can be placed before `V` (5) and `X` (10) to make 4 and 9.
* `X` can be placed before `L` (50) and `C` (100) to make 40 and 90.
* `C` can be placed before `D` (500) and `M` (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
**Example 1:**
**Input:** s = "III "
**Output:** 3
**Explanation:** III = 3.
**Example 2:**
**Input:** s = "LVIII "
**Output:** 58
**Explanation:** L = 50, V= 5, III = 3.
**Example 3:**
**Input:** s = "MCMXCIV "
**Output:** 1994
**Explanation:** M = 1000, CM = 900, XC = 90 and IV = 4.
**Constraints:**
* `1 <= s.length <= 15`
* `s` contains only the characters `('I', 'V', 'X', 'L', 'C', 'D', 'M')`.
* It is **guaranteed** that `s` is a valid roman numeral in the range `[1, 3999]`. | Problem is simpler to solve by working the string from back to front and using a map. |
python3 | fast | space-O(1) | time - O(n) | roman-to-integer | 0 | 1 | ```\nclass Solution:\n def romanToInt(self, s: str) -> int:\n a={"I":1,"V":5,"X":10,"L":50,"C":100,"D":500,"M":1000}\n sum=0 \n x=0\n while x<len(s):\n if x<len(s)-1 and a[s[x]]<a[s[x+1]]:\n sum += (a[s[x+1]] - a[s[x]])\n x += 2\n else:\n sum += a[s[x]]\n x += 1\n return sum\n``` | 8 | Roman numerals are represented by seven different symbols: `I`, `V`, `X`, `L`, `C`, `D` and `M`.
**Symbol** **Value**
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, `2` is written as `II` in Roman numeral, just two ones added together. `12` is written as `XII`, which is simply `X + II`. The number `27` is written as `XXVII`, which is `XX + V + II`.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not `IIII`. Instead, the number four is written as `IV`. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as `IX`. There are six instances where subtraction is used:
* `I` can be placed before `V` (5) and `X` (10) to make 4 and 9.
* `X` can be placed before `L` (50) and `C` (100) to make 40 and 90.
* `C` can be placed before `D` (500) and `M` (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
**Example 1:**
**Input:** s = "III "
**Output:** 3
**Explanation:** III = 3.
**Example 2:**
**Input:** s = "LVIII "
**Output:** 58
**Explanation:** L = 50, V= 5, III = 3.
**Example 3:**
**Input:** s = "MCMXCIV "
**Output:** 1994
**Explanation:** M = 1000, CM = 900, XC = 90 and IV = 4.
**Constraints:**
* `1 <= s.length <= 15`
* `s` contains only the characters `('I', 'V', 'X', 'L', 'C', 'D', 'M')`.
* It is **guaranteed** that `s` is a valid roman numeral in the range `[1, 3999]`. | Problem is simpler to solve by working the string from back to front and using a map. |
3 Solutions for Roman to Integer (Python3 🐍) | roman-to-integer | 0 | 1 | \n**1.First Solution (list comprehantion)**\n* Runtime: *55ms -> 121ms*\n* Memory runtime: 13.7MB -> 14MB\n\n**2. Secound Solution (for loop)**\n* Runtime: 48ms -> 109ms\n* Memory runtime: 13.8MB -> 14MB\n\n\n**3. Third Solution (enum, for fun)**\n* Runtime: 69ms -> 179ms\n* Memory runtime: 13.9MB -> 14.1MB\n\n\n\n\n \n```\nfrom enum import Enum\nclass RomanType(Enum):\n I = 1\n V = 5\n X = 10\n L = 50\n C = 100\n D = 500\n M = 1000\n\t\nclass Solution:\n def romanToInt_I(self, s: str) ->int:\n # create a dictionary translation\n roman_to_int_dict = {\'I\':1, "V":5, \'X\':10, \'L\':50, \'C\':100, \'D\':500, \'M\':1000}\n \n # convert roman to int\n list_of_num = [roman_to_int_dict[char] for char in s]\n \n # modify numbers based on current number and last number\n list_of_num = [list_of_num[index] - 2 * list_of_num[index - 1] \n if list_of_num[index - 1] < list_of_num[index] and index != 0\n else list_of_num[index]\n for index in range(len(list_of_num))]\n # return sum of list\n return sum(list_of_num)\n \n def romanToInt_II(self, s: str) ->int:\n # create a dictionary translation\n roman_to_int_dict = {\'I\':1, "V":5, \'X\':10, \'L\':50, \'C\':100, \'D\':500, \'M\':1000}\n \n\t sum = 0\n for index, char in enumerate(s):\n\t\t\t# get current and last values\n current_num = roman_to_int_dict[char]\n last_num = roman_to_int_dict[s[index - 1]]\n \n\t\t\t# add to sum based on case\n if index != 0 and last_num < current_num:\n sum += current_num - 2 * last_num\n else:\n sum += current_num\n \n return sum\n \n def romanToInt_III(self, s: str) ->int:\n sum = 0\n \n for index, char in enumerate(s):\n\t\t\t# get values by enum\n current_num = RomanType[char].value\n last_num = RomanType[s[index - 1]].value\n\t\t\t\n\t\t\t# add to sum based on case\n if index != 0 and last_num < current_num:\n sum += current_num - 2 * last_num\n else:\n sum += current_num\n \n return sum\n\n \n``` | 3 | Roman numerals are represented by seven different symbols: `I`, `V`, `X`, `L`, `C`, `D` and `M`.
**Symbol** **Value**
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, `2` is written as `II` in Roman numeral, just two ones added together. `12` is written as `XII`, which is simply `X + II`. The number `27` is written as `XXVII`, which is `XX + V + II`.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not `IIII`. Instead, the number four is written as `IV`. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as `IX`. There are six instances where subtraction is used:
* `I` can be placed before `V` (5) and `X` (10) to make 4 and 9.
* `X` can be placed before `L` (50) and `C` (100) to make 40 and 90.
* `C` can be placed before `D` (500) and `M` (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
**Example 1:**
**Input:** s = "III "
**Output:** 3
**Explanation:** III = 3.
**Example 2:**
**Input:** s = "LVIII "
**Output:** 58
**Explanation:** L = 50, V= 5, III = 3.
**Example 3:**
**Input:** s = "MCMXCIV "
**Output:** 1994
**Explanation:** M = 1000, CM = 900, XC = 90 and IV = 4.
**Constraints:**
* `1 <= s.length <= 15`
* `s` contains only the characters `('I', 'V', 'X', 'L', 'C', 'D', 'M')`.
* It is **guaranteed** that `s` is a valid roman numeral in the range `[1, 3999]`. | Problem is simpler to solve by working the string from back to front and using a map. |
⭐C#, Java, Python3,JavaScript Solution (Easy) | roman-to-integer | 1 | 1 | ### C#,Java,Python3,JavaScript different solution with explanation\n**\u2B50[https://zyrastory.com/en/coding-en/leetcode-en/leetcode-13-roman-to-integer-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-13-roman-to-integer-solution-and-explanation-en/)\u2B50**\n\n**\uD83E\uDDE1See next question solution - [Zyrastory-Longest Common Prefix](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-14-longest-common-prefix-solution-and-explanation-en/)**\n\nIf you got any problem about the explanation or you need other programming language solution, please feel free to leave your comment.\n\n**Thanks!** | 16 | Roman numerals are represented by seven different symbols: `I`, `V`, `X`, `L`, `C`, `D` and `M`.
**Symbol** **Value**
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, `2` is written as `II` in Roman numeral, just two ones added together. `12` is written as `XII`, which is simply `X + II`. The number `27` is written as `XXVII`, which is `XX + V + II`.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not `IIII`. Instead, the number four is written as `IV`. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as `IX`. There are six instances where subtraction is used:
* `I` can be placed before `V` (5) and `X` (10) to make 4 and 9.
* `X` can be placed before `L` (50) and `C` (100) to make 40 and 90.
* `C` can be placed before `D` (500) and `M` (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
**Example 1:**
**Input:** s = "III "
**Output:** 3
**Explanation:** III = 3.
**Example 2:**
**Input:** s = "LVIII "
**Output:** 58
**Explanation:** L = 50, V= 5, III = 3.
**Example 3:**
**Input:** s = "MCMXCIV "
**Output:** 1994
**Explanation:** M = 1000, CM = 900, XC = 90 and IV = 4.
**Constraints:**
* `1 <= s.length <= 15`
* `s` contains only the characters `('I', 'V', 'X', 'L', 'C', 'D', 'M')`.
* It is **guaranteed** that `s` is a valid roman numeral in the range `[1, 3999]`. | Problem is simpler to solve by working the string from back to front and using a map. |
✅Python3 || C++|| Java✅ 19 ms || Beats 99.91% | longest-common-prefix | 1 | 1 | # Please UPVOTE\uD83D\uDE0A\n\n\nThis code implements the longestCommonPrefix function that takes a list of strings v as input and returns the longest common prefix of all the strings. Here is an explanation of how the code works:\n\n1. Initialize an empty string ans to store the common prefix.\n2. Sort the input list v lexicographically. This step is necessary because the common prefix should be common to all the strings, so we need to find the common prefix of the first and last string in the sorted list.\n3. Iterate through the characters of the first and last string in the sorted list, stopping at the length of the shorter string.\n4. If the current character of the first string is not equal to the current character of the last string, return the common prefix found so far.\n5. Otherwise, append the current character to the ans string.\n6. Return the ans string containing the longest common prefix.\n\nNote that the code assumes that the input list v is non-empty, and that all the strings in v have at least one character. If either of these assumptions is not true, the code may fail.\n# Python3\n```\nclass Solution:\n def longestCommonPrefix(self, v: List[str]) -> str:\n ans=""\n v=sorted(v)\n first=v[0]\n last=v[-1]\n for i in range(min(len(first),len(last))):\n if(first[i]!=last[i]):\n return ans\n ans+=first[i]\n return ans \n\n```\n# C++\n```\nclass Solution {\npublic:\n string longestCommonPrefix(vector<string>& v) {\n string ans="";\n sort(v.begin(),v.end());\n int n=v.size();\n string first=v[0],last=v[n-1];\n for(int i=0;i<min(first.size(),last.size());i++){\n if(first[i]!=last[i]){\n return ans;\n }\n ans+=first[i];\n }\n return ans;\n }\n};\n```\n# Java \n```\nclass Solution {\n public String longestCommonPrefix(String[] v) {\n StringBuilder ans = new StringBuilder();\n Arrays.sort(v);\n String first = v[0];\n String last = v[v.length-1];\n for (int i=0; i<Math.min(first.length(), last.length()); i++) {\n if (first.charAt(i) != last.charAt(i)) {\n return ans.toString();\n }\n ans.append(first.charAt(i));\n }\n return ans.toString();\n }\n}\n```\n | 1,587 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
[VIDEO] Visualization of Vertical Scanning Solution | longest-common-prefix | 0 | 1 | https://youtube.com/watch?v=SiNDN2M4dtQ\n\nThis solution is the <b>vertical scanning</b> approach that is discussed in the official solution, slightly modified for Python. The idea is to scan the the first character of every word, then the second character, etc. until a mismatch is found. At that point, we return a slice of the string which is the longest common prefix.\n\nThis is superior to horizontal scanning because even if a very short word is included in the array, the algorithm won\'t do any extra work scanning the longer words and will still end when the end of the shortest word is reached.\n\n# Code\n```\nclass Solution(object):\n def longestCommonPrefix(self, strs):\n if len(strs) == 0:\n return ""\n\n base = strs[0]\n for i in range(len(base)):\n for word in strs[1:]:\n if i == len(word) or word[i] != base[i]:\n return base[0:i]\n\n return base\n \n``` | 9 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
Longest Common Prefix!!! | longest-common-prefix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this function is to find the longest common prefix among a list of strings. the "prefix" refers to the initial sequence of characters that all strings in the given list share in common. More formally, it is the sequence of characters that appear at the beginning of each string in the list. The idea is to iterate through the characters of the string with the minimum length (assuming it\'s the shortest string in the list) and check if the corresponding characters in all strings at that position are the same.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize an empty string s to store the common prefix and get the length l of the shortest string in the list.\n- Sort the list of strings.\n- Iterate through the characters of the first string (since it\'s sorted, it will be the lexicographically smallest).\n - Check if the character at the current position is the same in both the first and last strings in the sorted list.\n - If it is the same for all strings, append the character to the common prefix s.\n - If not, break out of the loop.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this algorithm is O(n * m), where n is the number of strings in the list, and m is the length of the shortest string. This is because, in the worst case, you may need to iterate through all characters of the shortest string for each string in the list.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(m), where m is the length of the shortest string. This is because the additional space used is for the s variable, which stores the common prefix.\n# Code\n```\nclass Solution:\n def longestCommonPrefix(self, strs: List[str]) -> str:\n # Initialize an empty string to store the common prefix\n s = ""\n # Get the length of the shortest string in the list\n l = len(min(strs, key=len))\n \n # Sort the list of strings lexicographically\n strs.sort()\n \n # Iterate through the characters of the shortest string\n for i in range(l):\n # Check if the character at the current position is the same in the first and last strings\n if strs[0][i] == strs[-1][i]:\n # If it\'s the same for all strings, append the character to the common prefix\n s += strs[0][i]\n else:\n # If not, break out of the loop\n break\n \n # Return the longest common prefix\n return s\n\n``` | 4 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
Longest Common Prefix in Python | longest-common-prefix | 0 | 1 | # Intuition\nCompare each letter of each word to check if they match, and add them to an empty string until you hit a character that doesn\'t match. Return the string obtained so far.\n\n# Approach\nInitialize an empty string. Zip the list, so you get the first characters of each word together in a tuple, the second letters in another tuple, and so on. Convert each such tuple into a set, and check if the length of the set is 1 - to understand if the elements were same (as sets store only 1 instance of a repeated element). If the length of the set is 1, add the first element of the tuple (any element is fine, as all elements are same but we take the first element just to be cautious) to the empty string. If the length of a set is not 1, return the string as is. Finally, return the string obtained thus far.\n\n# Complexity\n- Time complexity:\n\n\n- Space complexity:\n\n\n# Code\n```\nclass Solution:\n def longestCommonPrefix(self, strs: List[str]) -> str:\n res = ""\n for a in zip(*strs):\n if len(set(a)) == 1: \n res += a[0]\n else: \n return res\n return res\n \n``` | 105 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
Python & startswith | longest-common-prefix | 0 | 1 | ```\nclass Solution:\n def longestCommonPrefix(self, strs: List[str]) -> str:\n \n pre = strs[0]\n \n for i in strs:\n while not i.startswith(pre):\n pre = pre[:-1]\n \n return pre \n``` | 150 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
[Python3] list(zip(*str)) | longest-common-prefix | 0 | 1 | * list(zip(*strs))\nstrs = ["flower","flow","flight"]\n```\nstrs = ["flower","flow","flight"]\nl = list(zip(*strs))\n>>> l = [(\'f\', \'f\', \'f\'), (\'l\', \'l\', \'l\'), (\'o\', \'o\', \'i\'), (\'w\', \'w\', \'g\')]\n```\n```\nclass Solution:\n def longestCommonPrefix(self, strs: List[str]) -> str:\n l = list(zip(*strs))\n prefix = ""\n for i in l:\n if len(set(i))==1:\n prefix += i[0]\n else:\n break\n return prefix\n```\n* traditional scan vertically\n```\n i 0 1 2 3 4 5\n 0 f l o w e r\n 1\t f l o w\n 2\t f l i g h t\n\t\t\nWe choose the first string in the list as a reference. in this case is str[0] = "flower"\nthe outside for-loop go through each character of the str[0] or "flower". f->l->o->w->e->r\nthe inside for-loop, go through the words, in this case is flow, flight.\n\n\nstrs[j][i] means the the i\'s character of the j words in the strs.\n\nthere are 3 cases when we proceed the scan:\n\ncase 1: strs[j][i] = c, strs[1][2] = \'o\' and strs[0][2] = \'o\'; keep going;\ncase 2: strs[j][i] != c, strs[2][2] = \'i\' and strs[0][2] = \'o\'; break the rule, we can return strs[j][:i]. when comes to slicing a string, [:i] won\'t include the index i;\ncase 3: i = len(strs[j]) which means current word at strs[j] doesn\'t have character at index i, since it\'s 0 based index. the lenght equals i, the index ends at i - 1; break the rule, we can return.\n\n \n```\n\n\n```\nclass Solution:\n def longestCommonPrefix(self, strs: List[str]) -> str:\n if strs == None or len(strs) == 0: return ""\n for i in range(len(strs[0])): \n c = strs[0][i]// \n for j in range(1,len(strs)):\n if i == len(strs[j]) or strs[j][i] != c:\n return strs[0][:i]\n return strs[0] if strs else ""\n``` | 215 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
⭐C#,Java,Python3,JavaScript Solution ( Explanation ) | longest-common-prefix | 1 | 1 | **Which have included C#, Java, Python3,JavaScript solutions**\n**\u2B50[https://zyrastory.com/en/coding-en/leetcode-en/leetcode-14-longest-common-prefix-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-14-longest-common-prefix-solution-and-explanation-en/)\u2B50**\n\n\n#### Example : Java Code \u27A1 Runtime : 1ms\n```\nclass Solution {\n public String longestCommonPrefix(String[] strs) {\n for (int i = 0; i < strs[0].length(); i++) \n {\n char tmpChar = strs[0].charAt(i); \n for (int j = 0; j < strs.length; j++) \n {\n if (strs[j].length() == i || strs[j].charAt(i) != tmpChar) \n {\n return strs[0].substring(0, i);\n }\n }\n }\n return strs[0]; \n }\n}\n```\n**You can find a faster Java solution in the link.**\n\n\nIf you got any problem about the explanation or you need other programming language solution, please feel free to leave your comment.\n\n**\uD83E\uDDE1See more LeetCode solution : [Zyrastory - LeetCode Solution](https://zyrastory.com/en/category/coding-en/leetcode-en/)** | 11 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
Python Solution!! | longest-common-prefix | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def longestCommonPrefix(self, strs: List[str]) -> str:\n\n minimun_word: int = len(min(strs, key = len))\n preffix: str = ""\n\n for index in range(minimun_word):\n \n pivot: str = strs[0][index]\n window: list = [word[index] for word in strs] \n \n if all([char == pivot for char in window]):\n preffix += pivot\n else:\n break\n \n return preffix\n\n``` | 2 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
Python | Brilliant Approach taught by my bf xD | longest-common-prefix | 0 | 1 | # Intuition\n**EDIT** - Earlier I used sorting, which took O(M * NLOGN) complexity.Instead we can use min() and max() , which takes O(N*M) time.complexity. (N is no.of elements in the array and M is size of the string)\n\nIf you sort the given array (lexicographically), the **first** and **last** word will be the least similar (i.e, they vary the most)\n- It is enough if you find the common prefix between the **first** and **last** word ( need not consider other words in the array )\n\n**Example:** arr = ["aad","aaf", "aaaa", "af"]\n1) Sorted arr is ["aaaa", "aad", "aaf", "af"]\n2) *first* = "aaaa", *last* = "af"\n3) Common prefix of *first* and *last* is ans = "a"\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) **Sort** the given array\n2) Take the **first** and **last** word of the array\n3) Find the common **prefix** of the first and last word\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*M) - since use min() and max() in python, where N is no.of elements in the array and M is size of the string\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) - no extra space is used\n\n# Code\n```\nclass Solution:\n def longestCommonPrefix(self, strs: List[str]) -> str:\n first, last = min(strs), max(strs)\n prefix = \'\'\n for ind in range(min(len(first), len(last))):\n if first[ind] != last[ind]:\n break\n prefix += first[ind]\n\n return prefix\n``` | 23 | Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string `" "`.
**Example 1:**
**Input:** strs = \[ "flower ", "flow ", "flight "\]
**Output:** "fl "
**Example 2:**
**Input:** strs = \[ "dog ", "racecar ", "car "\]
**Output:** " "
**Explanation:** There is no common prefix among the input strings.
**Constraints:**
* `1 <= strs.length <= 200`
* `0 <= strs[i].length <= 200`
* `strs[i]` consists of only lowercase English letters. | null |
[Python] 5 Easy Steps - Beats 97.4% - Annotated | 3sum | 0 | 1 | ```python\ndef threeSum(self, nums: List[int]) -> List[List[int]]:\n\n\tres = set()\n\n\t#1. Split nums into three lists: negative numbers, positive numbers, and zeros\n\tn, p, z = [], [], []\n\tfor num in nums:\n\t\tif num > 0:\n\t\t\tp.append(num)\n\t\telif num < 0: \n\t\t\tn.append(num)\n\t\telse:\n\t\t\tz.append(num)\n\n\t#2. Create a separate set for negatives and positives for O(1) look-up times\n\tN, P = set(n), set(p)\n\n\t#3. If there is at least 1 zero in the list, add all cases where -num exists in N and num exists in P\n\t# i.e. (-3, 0, 3) = 0\n\tif z:\n\t\tfor num in P:\n\t\t\tif -1*num in N:\n\t\t\t\tres.add((-1*num, 0, num))\n\n\t#3. If there are at least 3 zeros in the list then also include (0, 0, 0) = 0\n\tif len(z) >= 3:\n\t\tres.add((0,0,0))\n\n\t#4. For all pairs of negative numbers (-3, -1), check to see if their complement (4)\n\t# exists in the positive number set\n\tfor i in range(len(n)):\n\t\tfor j in range(i+1,len(n)):\n\t\t\ttarget = -1*(n[i]+n[j])\n\t\t\tif target in P:\n\t\t\t\tres.add(tuple(sorted([n[i],n[j],target])))\n\n\t#5. For all pairs of positive numbers (1, 1), check to see if their complement (-2)\n\t# exists in the negative number set\n\tfor i in range(len(p)):\n\t\tfor j in range(i+1,len(p)):\n\t\t\ttarget = -1*(p[i]+p[j])\n\t\t\tif target in N:\n\t\t\t\tres.add(tuple(sorted([p[i],p[j],target])))\n\n\treturn res\n```\n<img src = "https://assets.leetcode.com/users/images/86c4a895-77e4-45ac-bebe-21a543b1cfe8_1594231844.7854018.png" width = "500px"> | 888 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Beats : 99.48% [44/145 Top Interview Question] | 3sum | 0 | 1 | # Intuition\n*3 solutions, Each latter is more optimized!*\n\n# Complexity\n- Time complexity:\nO(n^2)\n ***Note, these are worst case complexity, optimization improves the runtime.***\n\n- Space complexity:\nO(n)\n ***Note, This is the dominant or the higher order space complexity, while optimizing the space incurred might be higher but it will always be linear to the input size..***\n\n\n# Approach - 1\nThe 3-sum problem using the two-pointer approach. Here\'s a breakdown of how it works:\n\n1. The function `threeSum` takes an input list of integers called `nums` and returns a list of lists, representing the triplets that satisfy the 3-sum condition.\n\n2. The first step is to sort the input array `nums` in ascending order using the `sort()` method. Sorting the array is necessary to apply the two-pointer approach efficiently.\n\n3. A set called `triplets` is initialized to store the unique triplets that satisfy the 3-sum condition. Using a set helps avoid duplicate entries in the final result.\n\n4. The code then proceeds with a loop that iterates through each element of the array, up to the second-to-last element (`len(nums) - 2`). This is because we need at least three elements to form a triplet.\n\n5. Within the loop, the current element at index `i` is assigned to the variable `firstNum`. Two pointers, `j` and `k`, are initialized. `j` starts from `i + 1` (the element next to `firstNum`), and `k` starts from the last element of the array.\n\n6. A while loop is used to find the pairs (`secondNum` and `thirdNum`) that can form a triplet with `firstNum`. The loop continues as long as `j` is less than `k`.\n\n7. Inside the while loop, the current values at indices `j` and `k` are assigned to `secondNum` and `thirdNum`, respectively.\n\n8. The `potentialSum` variable stores the sum of `firstNum`, `secondNum`, and `thirdNum`.\n\n9. If `potentialSum` is greater than 0, it means the sum is too large. In this case, we decrement `k` to consider a smaller value.\n\n10. If `potentialSum` is less than 0, it means the sum is too small. In this case, we increment `j` to consider a larger value.\n\n11. If `potentialSum` is equal to 0, it means we have found a triplet that satisfies the 3-sum condition. The triplet `(firstNum, secondNum, thirdNum)` is added to the `triplets` set. Additionally, both `j` and `k` are incremented and decremented, respectively, to explore other possible combinations.\n\n12. After the loop ends, the function returns the `triplets` set, which contains all the unique triplets that sum to zero.\n\n# Code : Beats 23.46% *(Easy to understand)*\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n nums.sort()\n triplets = set()\n for i in range(len(nums) - 2):\n firstNum = nums[i]\n j = i + 1\n k = len(nums) - 1\n while j < k:\n secondNum = nums[j]\n thirdNum = nums[k]\n\n potentialSum = firstNum + secondNum + thirdNum \n if potentialSum > 0:\n k -= 1\n elif potentialSum < 0:\n j += 1\n else:\n triplets.add((firstNum , secondNum ,thirdNum))\n j += 1\n k -= 1\n return triplets\n```\n\n# Approach - 2\nThis is an *`enhanced version`* of the previous solution. It includes additional checks to skip duplicate values and improve efficiency. Here\'s an explanation of the changes and the updated time and space complexity:\n\nChanges in the Code:\n1. Right after sorting the array, the code includes an `if` statement to check for duplicate values of the first number. If `nums[i]` is the same as `nums[i - 1]`, it means we have already processed a triplet with the same first number, so we skip the current iteration using the `continue` statement.\n\n2. Inside the `else` block where a triplet is found, the code includes two additional `while` loops to skip duplicate values of the second and third numbers. These loops increment `j` and decrement `k` until the next distinct values are encountered.\n\n\nOverall, the time complexity is improved due to skipping duplicate values, resulting in a more efficient execution. The time complexity remains O(n^2) in the worst case but with better average-case performance.\n\n\n# Code: Optimized, Beats: 57.64%\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n nums.sort()\n triplets = set()\n for i in range(len(nums) - 2):\n if i > 0 and nums[i] == nums[i - 1]:\n continue # Skip duplicate values of the first number\n firstNum = nums[i]\n j, k = i + 1, len(nums) - 1\n while j < k:\n secondNum, thirdNum = nums[j], nums[k]\n potentialSum = firstNum + secondNum + thirdNum \n if potentialSum > 0:\n k -= 1\n elif potentialSum < 0:\n j += 1\n else:\n triplets.add((firstNum, secondNum, thirdNum))\n j, k = j + 1, k - 1\n while j < k and nums[j] == nums[j - 1]:\n j += 1 # Skip duplicate values of the second number\n while j < k and nums[k] == nums[k + 1]:\n k -= 1 # Skip duplicate values of the third number\n return triplets\n```\n\n# Approach - 3\n\nThis code is another implementation of the Three Sum problem that uses `defaultdict` from the `collections` module. Here\'s an explanation of the code:\n\n1. The code initializes three variables: `negative`, `positive`, and `zeros` as defaultdicts with a default value of 0. These dictionaries will store the count of negative numbers, positive numbers, and zeros, respectively.\n\n2. The `for` loop iterates through each number in the input `nums` list and increments the count of the corresponding dictionary based on whether the number is negative, positive, or zero.\n\n3. The code initializes an empty list called `result`, which will store the triplets that add up to zero.\n\n4. If there are one or more zeros in the input list, the code loops through the negative numbers and checks if the complement of the negative number exists in the positive numbers dictionary. If it does, the code appends a triplet of (0, n, -n) to the `result` list.\n\n5. If there are more than two zeros in the input list, the code appends a triplet of (0,0,0) to the `result` list.\n\n6. The code loops through pairs of negative and positive dictionaries and iterates through each pair of keys `(j, k)` in the dictionary. Then, it loops through each pair of keys `(j2, k2)` in the same dictionary, starting from the current index in the outer loop to avoid duplicates. Finally, the code checks if the complement of the sum of the two keys exists in the opposite dictionary (e.g., if the current loop is on the negative dictionary, it checks if the complement exists in the positive dictionary). If it does, the code appends a triplet of `(j, j2, -j-j2)` to the `result` list.\n\n7. The `result` list is returned at the end of the function.\n\n\n# Code - Beats: 99.48\n```\nfrom collections import defaultdict\n\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n negative = defaultdict(int)\n positive = defaultdict(int)\n zeros = 0\n for num in nums:\n if num < 0:\n negative[num] += 1\n elif num > 0:\n positive[num] += 1\n else:\n zeros += 1\n \n result = []\n if zeros:\n for n in negative:\n if -n in positive:\n result.append((0, n, -n)) \n if zeros > 2:\n result.append((0,0,0))\n\n for set1, set2 in ((negative, positive), (positive, negative)):\n set1Items = list(set1.items())\n for i, (j, k) in enumerate(set1Items):\n for j2, k2 in set1Items[i:]:\n if j != j2 or (j == j2 and k > 1):\n if -j-j2 in set2:\n result.append((j, j2, -j-j2))\n return result\n```\n\n# Above Complexity: [in Depth]\n\n`Time Complexity`:\n1. The `for` loop that counts the occurrence of each number in the input list takes `O(n)` time.\n\n2. The loop that checks for zero triplets takes `O(n)` time in the worst case, as it iterates through each negative number and checks if its complement exists in the positive numbers dictionary.\n\n3. The loop that checks for non-zero triplets takes `O(n^2)` time in the worst case, as it iterates through each pair of keys in each dictionary and checks if their complement exists in the opposite dictionary.\n\n4. The overall `time complexity` of the function is `O(n^2)`, as the loop that takes the most time is the one that checks for non-zero triplets.\n\n`Space Complexity`:\n1. The space complexity is `O(n)` for the three `defaultdict` dictionaries, as they store the count of each number in the input list.\n\n2. The space complexity of the `result` list is also `O(n)` in the worst case, as there can be up to `O(n)` triplets that add up to zero\n\n\nIn summary, this implementation of the Three Sum problem also has a time complexity of `O(n^2)` and a space complexity of `O(n)`. However, it uses `defaultdict` to count the occurrence of each number in the input list and improves the efficiency of checking for zero triplets by using a dictionary lookup instead of iterating through the list. | 114 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
[VIDEO] Visualization of O(n^2) Solution (Two Pointers) | 3sum | 0 | 1 | https://youtu.be/IIxoo93bmPQ\n\nThis problem is similar to Two Sum, but the main differentiator is that there can now be multiple solutions and we must not return duplicate ones. This requires us to use a different approach, since Two Sum assumes that there is only one solution.\n\nThe key is to sort the array first. We then use an outer loop to fix one of the numbers and use a two pointer approach to find all solutions for that number. The pointers, `l` and `r`, start at the ends of the array and work themselves inwards.\n\nAt each iteration, we calculate the total and compare it to 0. If the total is less than zero, then since we need to make the total <i>larger</i> and the array is sorted, the only thing we can do is move `l` up (moving `r` down would only make the total <i>smaller</i>). Similarly, if the total is greater than 0, then we just move `r` down.\n\nIf the total is equal to 0, then that means we\'ve found a solution, so we append the triplet to our answer array and then keep moving `l` and `r` inwards until they both get to different numbers.\n\n# Code\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n nums.sort()\n answer = []\n for i in range(len(nums) - 2):\n if nums[i] > 0:\n break\n if i > 0 and nums[i] == nums[i-1]:\n continue\n l = i + 1\n r = len(nums) - 1\n while l < r:\n total = nums[i] + nums[l] + nums[r]\n if total < 0:\n l += 1\n elif total > 0:\n r -= 1\n else:\n triplet = [nums[i], nums[l], nums[r]]\n answer.append(triplet)\n while l < r and nums[l] == triplet[1]:\n l += 1\n while l < r and nums[r] == triplet[2]:\n r -= 1\n return answer\n``` | 1 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Python & Java Solution - 100% EXPLAINED ✔ | 3sum | 0 | 1 | # PYTHON CODE\n\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]: \n nums.sort() # sorting cause we need to avoid duplicates, with this duplicates will be near to each other\n l=[]\n for i in range(len(nums)): #this loop will help to fix the one number i.e, i\n if i>0 and nums[i-1]==nums[i]: #skipping if we found the duplicate of i\n continue \n\t\t\t\n\t\t\t#NOW FOLLOWING THE RULE OF TWO POINTERS AFTER FIXING THE ONE VALUE (i)\n j=i+1 #taking j pointer larger than i (as said in ques)\n k=len(nums)-1 #taking k pointer from last \n while j<k: \n s=nums[i]+nums[j]+nums[k] \n if s>0: #if sum s is greater than 0(target) means the larger value(from right as nums is sorted i.e, k at right) \n\t\t\t\t#is taken and it is not able to sum up to the target\n k-=1 #so take value less than previous\n elif s<0: #if sum s is less than 0(target) means the shorter value(from left as nums is sorted i.e, j at left) \n\t\t\t\t#is taken and it is not able to sum up to the target\n j+=1 #so take value greater than previous\n else:\n l.append([nums[i],nums[j],nums[k]]) #if sum s found equal to the target (0)\n j+=1 \n while nums[j-1]==nums[j] and j<k: #skipping if we found the duplicate of j and we dont need to check \n\t\t\t\t\t#the duplicate of k cause it will automatically skip the duplicate by the adjustment of i and j\n j+=1 \n return l\n```\n\n# JAVA CODE\n\n```\nclass Solution {\n public List<List<Integer>> threeSum(int[] nums) { \n List<List<Integer>> arr = new ArrayList<>();\n Arrays.sort(nums);\n for (int i=0; i<nums.length; i++){\n if (i>0 && nums[i] == nums[i-1]){\n continue;\n }\n int j = i+1;\n int k = nums.length - 1;\n while (j<k){\n int s = nums[i]+ nums[j]+ nums[k];\n if (s > 0){\n k -= 1;\n }\n else if (s < 0){\n j += 1;\n }\n else{\n arr.add(new ArrayList<>(Arrays.asList(nums[i],nums[j],nums[k]))); \n j+=1;\n while (j<k && nums[j] == nums[j-1]){\n j+=1;\n }\n }\n }\n }\n return arr;\n }\n}\n```\n**PLEASE UPVOTE IF YOU FOUND THE SOLUTION HELPFUL** | 123 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Python 3 pointer solution | 3sum | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n # sort the list in ascending order\n nums.sort()\n\n # initialize an empty list to store the triplets\n ans = []\n\n # get the length of the list\n n = len(nums)\n\n # set ptr1 to the first element of the list\n ptr1 = 0\n\n # iterate through the list with ptr1\n while ptr1 < n - 2:\n # skip over duplicates of nums[ptr1]\n if ptr1 > 0 and nums[ptr1] == nums[ptr1 - 1]:\n ptr1 += 1\n continue\n\n # exit early if nums[ptr1] is greater than 0\n if nums[ptr1] > 0:\n break\n\n # set ptr2 and ptr3\n ptr2, ptr3 = ptr1 + 1, n - 1\n\n while ptr2 < ptr3:\n # check for sum of 0\n sum_ = nums[ptr1] + nums[ptr2] + nums[ptr3]\n if sum_ == 0:\n ans.append([nums[ptr1], nums[ptr2], nums[ptr3]])\n ptr2 += 1\n ptr3 -= 1\n\n # skip over duplicates of nums[ptr2]\n while ptr2 < ptr3 and nums[ptr2] == nums[ptr2 - 1]:\n ptr2 += 1\n\n # skip over duplicates of nums[ptr3]\n while ptr2 < ptr3 and nums[ptr3] == nums[ptr3 + 1]:\n ptr3 -= 1\n\n # adjust ptr2 or ptr3 based on sum\n elif sum_ < 0:\n ptr2 += 1\n else:\n ptr3 -= 1\n\n ptr1 += 1\n\n return ans\n\n``` | 1 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Python Detailed Explanation | 3sum | 0 | 1 | # Explanation\nleft : leftmost index (iterate)\nmid : left + 1\nright: rightmost index (len(nums) - 1)\n\nThe main idea is that we fix `left` index. Then we find the sum of three values (left, mid, right) where `mid` is **initially `left + 1`** and `right` is **initially `len(nums) - 1`**.\n\n**If** the current sum is less than 0, we move `mid` to right by one since the `nums` are sorted in ascending order. \n**Else If** the current sum is greater than 0, we move `right` to left by one.\n\n**Else** where current sum is equal to 0, we add (left, mid, right) to result. And by moving `mid` to right by one and `right` to left by one at the same time, we keep going on finding other combinations. \n\n# Dealing with Duplicates\n\n`if left > 0 and nums[left] == nums[left-1]:\n continue`\nSince we fix `left` and find combinations by only moving `mid` and `right`, if current `left` value is equal to the previous one, the combinations would be the same. \n\n`while mid < right and nums[mid] == nums[mid+1]:\n mid+=1`\n`while mid < right and nums[right] == nums[right-1]:\n right -= 1`\n\nFor example, if nums = [-1,0,0,1,1,1,1], the first combination we can find is [-1,0,1] where "-1" is 0th index, "0" is 1st index and "1" is 3rd index. Another combination [-1,0,1] can be found if we take `left` and `mid` the same but `right` 4th index. However, since we do not want duplicates, we can skip all the same values of `mid` and `right` by using the code above.\n\n\n# Code\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n #-4 -1 -1 0 1 2\n nums.sort()\n result = []\n for left in range(len(nums)-2):\n if left > 0 and nums[left] == nums[left-1]:\n continue\n mid = left + 1\n right = len(nums) - 1\n\n while mid < right:\n summ = nums[left] + nums[mid] + nums[right]\n if summ < 0:\n mid += 1\n elif summ > 0:\n right -= 1\n else:\n result.append([nums[left],nums[mid],nums[right]]) \n while mid < right and nums[mid] == nums[mid+1]:\n mid+=1\n while mid < right and nums[right] == nums[right-1]:\n right -= 1\n\n mid +=1\n right -= 1\n return result\n\n\n\n \n \n \n \n \n \n \n``` | 3 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Python3 | 3sum | 0 | 1 | # Complexity\n- Time complexity: o(n^2)\n\n# Code\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n out = [] # Initialize an empty list to store the output triplets.\n nums.sort() # Sort the input list in ascending order.\n\n for i in range(0, len(nums) - 2): # Iterate through the list, considering each element as the first element of the triplet.\n if i > 0 and nums[i] == nums[i-1]: # Skip duplicate elements to avoid duplicate triplets.\n continue\n left, right = i + 1, len(nums) - 1 # Set the left and right pointers to the next and last elements respectively.\n while left < right: # Continue the loop until the pointers meet or cross each other.\n if (nums[i] + nums[left] + nums[right]) == 0: # If the sum of the three elements is zero:\n out.append([nums[i], nums[left], nums[right]]) # Add the triplet to the output list.\n left += 1 # Move the left pointer to the right.\n while nums[left] == nums[left-1] and left < right: # Skip duplicate elements to avoid duplicate triplets.\n left += 1\n if nums[i] + nums[left] + nums[right] < 0: # If the sum is less than zero:\n left += 1 # Move the left pointer to the right.\n else: # If the sum is greater than zero:\n right -= 1 # Move the right pointer to the left.\n return out # Return the list of unique triplets that sum to zero.\n\n``` | 1 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Beginners Brute Force to Optimised (Two Pointer) Solution | 3sum | 0 | 1 | ## Brute force approach\n\n### Code\n```python\n# Brute Force\n# TC: O(n*n*n)\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n arrLength = len(nums)\n\n ans = []\n\n\n for i_idx in range(0, arrLength - 2):\n for j_idx in range(i_idx + 1, arrLength - 1):\n for k_idx in range(j_idx + 1, arrLength):\n if nums[i_idx] + nums[j_idx] + nums[k_idx] == 0:\n # Sort the triplet and add it to the result if not already present\n triplet = sorted([nums[i_idx], nums[j_idx], nums[k_idx]])\n \n if triplet not in ans:\n ans.append(triplet)\n\n return ans\n```\n\n## Two Pointer (Optimised)\n\n### Code\n```python\n# TC: O(n*n):\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n arrLength = len(nums)\n\n nums.sort()\n\n ans = []\n\n for idx in range(0, arrLength):\n if idx > 0 and nums[idx] == nums[idx-1]:\n continue\n\n start, end = idx + 1, arrLength - 1\n \n while start < end:\n threeSum = nums[idx] + nums[start] + nums[end]\n\n if threeSum == 0:\n ans.append([nums[idx], nums[start], nums[end]])\n \n while (start < end) and nums[start] == nums[start + 1]:\n start += 1\n \n while (start < end) and nums[end] == nums[end - 1]:\n end -= 1\n\n start += 1\n end -= 1\n\n elif threeSum < 0:\n start += 1\n \n else:\n end -= 1\n\n return ans\n``` | 5 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Easy python solution || Using two Pointers | 3sum | 0 | 1 | # Code\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n nums.sort()\n dic={}\n lst=[]\n for i in range(len(nums)):\n low=i+1\n high=len(nums)-1\n while low<high:\n sm=nums[i]+nums[low]+nums[high]\n if sm==0:\n val=[nums[i],nums[low],nums[high]]\n if str(val) in dic:\n dic[str(val)]+=1\n else:\n dic[str(val)]=1\n lst.append(val)\n low+=1\n high-=1\n elif sm>0:\n high-=1\n else:\n low+=1\n return lst\n \n``` | 2 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Python code for N-Sum and bonus simplistic way of solving this question | 3sum | 0 | 1 | \n# Code\n```\nclass Solution:\n def threeSum(self, nums: List[int], target = 0) -> List[List[int]]:\n def findNsum(l, r, target, N, tmp, res):\n if r-l+1<N or N<2 or target < nums[l]*N or target > nums[r]*N:\n return\n if N == 2:\n while l < r:\n sum = nums[l]+nums[r]\n if sum==target:\n res.append(tmp+[nums[l], nums[r]])\n l+=1\n while l < r and nums[l] == nums[l-1]:\n l+=1\n elif sum < target:\n l+=1\n else:\n r-=1\n else:\n for i in range(l, r-1):\n if i==l or (i>l and nums[i]!=nums[i-1]):\n findNsum(i+1, r, target-nums[i],N-1, tmp+[nums[i]], res)\n nums.sort()\n res = []\n findNsum(0, len(nums) - 1, target, 3, [], res)\n return res\n \n```\n\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n res = set()\n pos, neg, zer = [], [], []\n for ele in nums:\n if ele < 0:\n neg.append(ele)\n elif ele == 0:\n zer.append(0)\n else:\n pos.append(ele)\n \n POS, NEG = set(pos), set(neg)\n\n if len(zer) >= 1:\n for target in POS:\n if -1 * target in NEG:\n res.add((target, 0, -1 * target))\n if len(zer) >= 3:\n res.add((0, 0, 0))\n \n for i in range(len(neg)):\n for j in range(i+1, len(neg)):\n target = neg[i] + neg[j]\n if -1*target in POS:\n res.add(tuple(sorted([neg[i], neg[j], -1 * target])))\n\n for i in range(len(pos)):\n for j in range(i+1, len(pos)):\n target = pos[i] + pos[j]\n if -1 * target in NEG:\n res.add(tuple(sorted([pos[i], pos[j], -1 * target])))\n \n return list(res)\n \n \n``` | 3 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
3Sum threesome | 3sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nit uses the 2sum but it calculates the target based on what the first number is. Then you use pointers to search for numbers that sum to the target. These 2 numbers in the list will be the other 2 numbers in the triplet. Keep searching the list until all unique pairs are found that add up to target.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n triplets = []\n n = len(nums)\n nums.sort()\n\n def sum2(i, target):\n low = i+1\n high = n-1\n while low < high:\n s = nums[low] + nums[high]\n if s > target:\n high -= 1\n elif s < target:\n low += 1\n else:\n triplets.append([nums[i], nums[low], nums[high]])\n\n low += 1\n high -= 1\n while low < high and nums[low] == nums[low-1]:\n low += 1\n \n for i in range(n - 2):\n if nums[i] > 0:\n break\n if i > 0 and nums[i] == nums[i - 1]:\n continue\n complement = -nums[i]\n sum2(i, complement)\n \n return triplets\n``` | 0 | Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
Notice that the solution set must not contain duplicate triplets.
**Example 1:**
**Input:** nums = \[-1,0,1,2,-1,-4\]
**Output:** \[\[-1,-1,2\],\[-1,0,1\]\]
**Explanation:**
nums\[0\] + nums\[1\] + nums\[2\] = (-1) + 0 + 1 = 0.
nums\[1\] + nums\[2\] + nums\[4\] = 0 + 1 + (-1) = 0.
nums\[0\] + nums\[3\] + nums\[4\] = (-1) + 2 + (-1) = 0.
The distinct triplets are \[-1,0,1\] and \[-1,-1,2\].
Notice that the order of the output and the order of the triplets does not matter.
**Example 2:**
**Input:** nums = \[0,1,1\]
**Output:** \[\]
**Explanation:** The only possible triplet does not sum up to 0.
**Example 3:**
**Input:** nums = \[0,0,0\]
**Output:** \[\[0,0,0\]\]
**Explanation:** The only possible triplet sums up to 0.
**Constraints:**
* `3 <= nums.length <= 3000`
* `-105 <= nums[i] <= 105` | So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand! For the two-sum problem, if we fix one of the numbers, say x, we have to scan the entire array to find the next numbery which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Python easy solution | letter-combinations-of-a-phone-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n digits_d = {\'2\':[\'a\',\'b\',\'c\'], \n \'3\':[\'d\',\'e\',\'f\'],\n \'4\':[\'g\',\'h\',\'i\'], \n \'5\':[\'j\',\'k\',\'l\'], \n \'6\':[\'m\',\'n\',\'o\'], \n \'7\':[\'p\',\'q\',\'r\',\'s\'],\n \'8\':[\'t\',\'u\',\'v\'],\n \'9\':[\'w\',\'x\',\'y\',\'z\']\n }\n res = []\n def find_n(ind,sub):\n if len(sub) ==len(digits):\n res.append(sub[:])\n return\n # if ind >= len(digits):\n # return \n dig = digits_d[digits[ind]]\n for i in dig:\n sub.append(i)\n find_n(ind+1,sub)\n sub.pop()\n \n if len(digits) >0:\n find_n(0,[])\n else:\n return []\n res1 = []\n for i in res:\n res1.append("".join(i))\n return res1\n \n``` | 1 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
📞 100% Backtracking & Iterative [VIDEO] Letter Combinations of a Phone Number | letter-combinations-of-a-phone-number | 1 | 1 | # Intuition\nGiven a string containing digits from 2-9 inclusive, we need to return all possible letter combinations that the number could represent, just like on a telephone\'s buttons. To accomplish this, we present two different approaches:\n\n1. **Backtracking Approach**: This approach leverages recursion to explore all possible combinations. We create a recursive function that takes the current combination and the next digits to explore. For each digit, we iterate through its corresponding letters and recursively explore the remaining digits. We append the combination when no more digits are left to explore.\n\n2. **Iterative Approach**: This approach builds the combinations iteratively without using recursion. We start with an empty combination and iteratively add letters for each digit in the input string. For each existing combination, we append each corresponding letter for the current digit, building new combinations.\n\n**Differences**:\n- The backtracking approach relies on recursion to explore all possible combinations, whereas the iterative approach builds combinations step by step using loops.\n- Both approaches have similar time complexity, but the iterative approach might save some function call overhead, leading to more efficient execution in some cases.\n\nDetailed explanations of both approaches, along with their corresponding code, are provided below. By presenting both methods, we offer a comprehensive view of how to tackle this problem, allowing for flexibility and understanding of different programming paradigms.\n\nhttps://youtu.be/Jobb9YUFUq0\n\n# Approach - Backtracking\n1. **Initialize a Mapping**: Create a dictionary that maps each digit from 2 to 9 to their corresponding letters on a telephone\'s buttons. For example, the digit \'2\' maps to "abc," \'3\' maps to "def," and so on.\n\n2. **Base Case**: Check if the input string `digits` is empty. If it is, return an empty list, as there are no combinations to generate.\n\n3. **Recursive Backtracking**:\n - **Define Recursive Function**: Create a recursive function, `backtrack`, that will be used to explore all possible combinations. It takes two parameters: `combination`, which holds the current combination of letters, and `next_digits`, which holds the remaining digits to be explored.\n - **Termination Condition**: If `next_digits` is empty, it means that all digits have been processed, so append the current `combination` to the result.\n - **Exploration**: If there are more digits to explore, take the first digit from `next_digits` and iterate over its corresponding letters in the mapping. For each letter, concatenate it to the current combination and recursively call the `backtrack` function with the new combination and the remaining digits.\n - **Example**: If the input is "23", the first recursive call explores all combinations starting with \'a\', \'b\', and \'c\' (from \'2\'), and the next level of recursive calls explores combinations starting with \'d\', \'e\', \'f\' (from \'3\'), building combinations like "ad," "ae," "af," "bd," "be," etc.\n\n4. **Result**: Once the recursive exploration is complete, return the collected combinations as the final result. By using recursion, we ensure that all possible combinations are explored, and the result includes all valid letter combinations that the input digits can represent.\n\n# Complexity\n- Time complexity: \\( O(4^n) \\), where \\( n \\) is the length of the input string. In the worst case, each digit can represent 4 letters, so there will be 4 recursive calls for each digit.\n- Space complexity: \\( O(n) \\), where \\( n \\) is the length of the input string. This accounts for the recursion stack space.\n\n# Code - Backtracking\n``` Python []\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if not digits:\n return []\n\n phone_map = {\n \'2\': \'abc\',\n \'3\': \'def\',\n \'4\': \'ghi\',\n \'5\': \'jkl\',\n \'6\': \'mno\',\n \'7\': \'pqrs\',\n \'8\': \'tuv\',\n \'9\': \'wxyz\'\n }\n\n def backtrack(combination, next_digits):\n if len(next_digits) == 0:\n output.append(combination)\n else:\n for letter in phone_map[next_digits[0]]:\n backtrack(combination + letter, next_digits[1:])\n\n output = []\n backtrack("", digits)\n return output\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<std::string> letterCombinations(std::string digits) {\n if (digits.empty()) return {};\n\n std::string phone_map[] = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};\n std::vector<std::string> output;\n backtrack("", digits, phone_map, output);\n return output;\n }\n\nprivate:\n void backtrack(std::string combination, std::string next_digits, std::string phone_map[], std::vector<std::string>& output) {\n if (next_digits.empty()) {\n output.push_back(combination);\n } else {\n std::string letters = phone_map[next_digits[0] - \'2\'];\n for (char letter : letters) {\n backtrack(combination + letter, next_digits.substr(1), phone_map, output);\n }\n }\n }\n};\n```\n``` Java []\nclass Solution {\n public List<String> letterCombinations(String digits) {\n if (digits.isEmpty()) return Collections.emptyList();\n\n String[] phone_map = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};\n List<String> output = new ArrayList<>();\n backtrack("", digits, phone_map, output);\n return output;\n }\n\n private void backtrack(String combination, String next_digits, String[] phone_map, List<String> output) {\n if (next_digits.isEmpty()) {\n output.add(combination);\n } else {\n String letters = phone_map[next_digits.charAt(0) - \'2\'];\n for (char letter : letters.toCharArray()) {\n backtrack(combination + letter, next_digits.substring(1), phone_map, output);\n }\n }\n }\n}\n```\n``` JavaSxript []\n/**\n * @param {string} digits\n * @return {string[]}\n */\nvar letterCombinations = function(digits) {\n if (digits.length === 0) return [];\n\n const phone_map = ["abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"];\n const output = [];\n backtrack("", digits, phone_map, output);\n return output;\n\n function backtrack(combination, next_digits, phone_map, output) {\n if (next_digits.length === 0) {\n output.push(combination);\n } else {\n const letters = phone_map[next_digits[0] - \'2\'];\n for (const letter of letters) {\n backtrack(combination + letter, next_digits.slice(1), phone_map, output);\n }\n }\n }\n};\n```\n``` C# []\npublic class Solution {\n public IList<string> LetterCombinations(string digits) {\n if (string.IsNullOrEmpty(digits)) return new List<string>();\n\n string[] phone_map = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};\n List<string> output = new List<string>();\n Backtrack("", digits, phone_map, output);\n return output;\n }\n\n private void Backtrack(string combination, string next_digits, string[] phone_map, List<string> output) {\n if (next_digits.Length == 0) {\n output.Add(combination);\n } else {\n string letters = phone_map[next_digits[0] - \'2\'];\n foreach (char letter in letters) {\n Backtrack(combination + letter, next_digits.Substring(1), phone_map, output);\n }\n }\n }\n}\n```\n``` Go []\nfunc letterCombinations(digits string) []string {\n\tif digits == "" {\n\t\treturn []string{}\n\t}\n\n\tphoneMap := []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}\n\tvar output []string\n\n\tvar backtrack func(combination string, nextDigits string)\n\tbacktrack = func(combination string, nextDigits string) {\n\t\tif nextDigits == "" {\n\t\t\toutput = append(output, combination)\n\t\t} else {\n\t\t\tletters := phoneMap[nextDigits[0]-\'2\']\n\t\t\tfor _, letter := range letters {\n\t\t\t\tbacktrack(combination+string(letter), nextDigits[1:])\n\t\t\t}\n\t\t}\n\t}\n\n\tbacktrack("", digits)\n\treturn output\n}\n```\n``` Rust []\nimpl Solution {\n pub fn letter_combinations(digits: String) -> Vec<String> {\n if digits.is_empty() {\n return vec![];\n }\n\n let phone_map = vec!["abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"];\n let mut output = Vec::new();\n\n fn backtrack(combination: String, next_digits: &str, phone_map: &Vec<&str>, output: &mut Vec<String>) {\n if next_digits.is_empty() {\n output.push(combination);\n } else {\n let letters = phone_map[next_digits.chars().nth(0).unwrap() as usize - \'2\' as usize];\n for letter in letters.chars() {\n let new_combination = combination.clone() + &letter.to_string();\n backtrack(new_combination, &next_digits[1..], phone_map, output);\n }\n }\n }\n\n backtrack(String::new(), &digits, &phone_map, &mut output);\n output\n }\n}\n```\nThis code can handle any input string containing digits from 2 to 9 and will return the possible letter combinations in any order. The function `backtrack` is used to handle the recursive exploration of combinations, and `phone_map` contains the mapping between digits and letters.\n\n## Performance - Backtracking\n\n| Language | Runtime (ms) | Beats (%) | Memory (MB) |\n|-------------|--------------|-----------|-------------|\n| C++ | 0 | 100.00 | 6.4 |\n| Go | 0 | 100.00 | 2.0 |\n| Rust | 1 | 82.50 | 2.1 |\n| Java | 5 | 50.30 | 41.6 |\n| Swift | 2 | 82.38 | 14.0 |\n| Python3 | 34 | 96.91 | 16.3 |\n| TypeScript | 49 | 96.36 | 44.3 |\n| JavaScript | 58 | 55.17 | 42.2 |\n| Ruby | 58 | 97.98 | 211.1 |\n| C# | 136 | 89.14 | 43.9 |\n\n# Video Iterative\nhttps://youtu.be/43x3sg_nND8\n\n# Approach - Iterative\n1. **Initialize a Mapping**: Create a dictionary that maps each digit from 2 to 9 to their corresponding letters on a telephone\'s buttons.\n2. **Base Case**: If the input string `digits` is empty, return an empty list.\n3. **Iteratively Build Combinations**: Start with an empty combination in a list and iteratively build the combinations by processing each digit in the input string.\n - For each existing combination, append each corresponding letter for the current digit, building new combinations.\n4. **Result**: Return the generated combinations as the final result.\n\n# Complexity\n- Time complexity: \\( O(4^n) \\), where \\( n \\) is the length of the input string. In the worst case, each digit can represent 4 letters.\n- Space complexity: \\( O(n) \\), where \\( n \\) is the length of the input string.\n\n# Code - Iterative\n``` Python []\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if not digits:\n return []\n\n phone_map = {\n \'2\': \'abc\',\n \'3\': \'def\',\n \'4\': \'ghi\',\n \'5\': \'jkl\',\n \'6\': \'mno\',\n \'7\': \'pqrs\',\n \'8\': \'tuv\',\n \'9\': \'wxyz\'\n }\n combinations = [""]\n\n for digit in digits:\n new_combinations = []\n for combination in combinations:\n for letter in phone_map[digit]:\n new_combinations.append(combination + letter)\n combinations = new_combinations\n\n return combinations\n```\n``` JavaScript []\nfunction letterCombinations(digits) {\n if (!digits) {\n return [];\n }\n\n const phoneMap = {\n \'2\': \'abc\',\n \'3\': \'def\',\n \'4\': \'ghi\',\n \'5\': \'jkl\',\n \'6\': \'mno\',\n \'7\': \'pqrs\',\n \'8\': \'tuv\',\n \'9\': \'wxyz\'\n };\n\n let combinations = [\'\'];\n\n for (const digit of digits) {\n const newCombinations = [];\n for (const combination of combinations) {\n for (const letter of phoneMap[digit]) {\n newCombinations.push(combination + letter);\n }\n }\n combinations = newCombinations;\n }\n\n return combinations;\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::vector<std::string> letterCombinations(std::string digits) {\n if (digits.empty()) return {};\n\n std::string phone_map[] = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};\n std::vector<std::string> combinations = {""};\n\n for (char digit : digits) {\n std::vector<std::string> new_combinations;\n for (std::string combination : combinations) {\n for (char letter : phone_map[digit - \'2\']) {\n new_combinations.push_back(combination + letter);\n }\n }\n combinations = new_combinations;\n }\n\n return combinations;\n }\n};\n```\n``` Go []\nfunc letterCombinations(digits string) []string {\n if digits == "" {\n return []string{}\n }\n\n phoneMap := []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}\n combinations := []string{""}\n\n for _, digit := range digits {\n newCombinations := []string{}\n for _, combination := range combinations {\n for _, letter := range phoneMap[digit-\'2\'] {\n newCombinations = append(newCombinations, combination+string(letter))\n }\n }\n combinations = newCombinations\n }\n\n return combinations\n}\n```\n\n\nIf you find the solution understandable and helpful, don\'t hesitate to give it an upvote. Engaging with the code across different languages might just lead you to discover new techniques and preferences! Happy coding! \uD83D\uDE80\uD83E\uDD80\uD83D\uDCDE\n | 92 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Simple Backtracking Algorithm|| Beats 90% 📶 || Python ✅ | letter-combinations-of-a-phone-number | 0 | 1 | # Intuition\nBacktracking Using Recursion.Iterative deepening search with depth as the length of given string ```s``` length.\n\n# Approach\nThe solution involves mainly **3 steps**:\n\n1. Starting the process with an empty string and index as 0 indicating the pointer digits string.\n2. Iterating it until we reach the last digit of the string `digit`.\n3. Backtracking the function to get all remaining possible combinations .\n\n# Complexity\n- Time complexity:O(2^n)\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def letterCombinations(self, s: str) -> List[str]:\n d={\'2\':[\'a\',\'b\',\'c\'],\'3\':[\'d\',\'e\',\'f\'],\'4\':[\'g\',\'h\',\'i\'],\'5\':[\'j\',\'k\',\'l\'],\'6\':[\'m\',\'n\',\'o\'],\'7\':[\'p\',\'q\',\'r\',\'s\'],\'8\':[\'t\',\'u\',\'v\'],\'9\':[\'w\',\'x\',\'y\',\'z\']}\n \n if s==\'\':\n return []\n l=[]\n\n def ids(st,index):\n if (index>=len(s)):\n l.append(st)\n return \n for i in d[s[index]]:\n ids(st+i,index+1)\n\n ids(\'\',0)\n return l\n``` | 1 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Simple solution | letter-combinations-of-a-phone-number | 0 | 1 | # Code\n```\nfrom typing import Dict, List\n\nclass Solution:\n \n def get_mapping(self) -> Dict[str, List[str]]:\n return {\n "2": ["a", "b", "c"],\n "3": ["d", "e", "f"],\n "4": ["g", "h", "i"],\n "5": ["j", "k", "l"],\n "6": ["m", "n", "o"],\n "7": ["p", "q", "r", "s"],\n "8": ["t", "u", "v"],\n "9": ["w", "x", "y", "z"]\n }\n \n def combine(self, x: List[str], y: List[str]) -> List[str]:\n out = []\n for a in x:\n for b in y:\n out.append(a + b)\n return(out)\n \n def letterCombinations(self, digits: str) -> List[str]:\n if digits == "":\n return []\n \n mapping = self.get_mapping()\n if len(digits) == 1:\n return mapping[digits]\n \n lists = []\n for d in digits:\n lists.append(mapping[d])\n\n while len(lists) >= 2:\n x = lists.pop(0)\n y = lists.pop(0)\n z = self.combine(x, y)\n lists.insert(0, z)\n return lists[0]\n\n``` | 1 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Go/Python O(n * 4^n) time | O(n * 4^n) space Recursion/Iterative | letter-combinations-of-a-phone-number | 0 | 1 | # Recursion\n- Time complexity: $$O(n * 4^n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n * 4^n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc letterCombinations(digits string) []string {\n answer := []string{}\n if len(digits) == 0{\n return answer\n }\n digit_to_letter := map[string]string{"2" : "abc",\n "3" : "def",\n "4" : "ghi",\n "5" : "jkl",\n "6" : "mno",\n "7" : "pqrs",\n "8" : "tuv",\n "9" : "wxyz"}\n curr := []rune{}\n var dfs func(int)\n dfs = func(idx int){\n if idx == len(digits){\n answer = append(answer,string(curr))\n return\n }\n for _,letter := range(digit_to_letter[string(digits[idx])]){\n curr = append(curr,letter)\n dfs(idx+1)\n curr = curr[:len(curr)-1]\n }\n }\n dfs(0)\n return answer\n}\n```\n```python []\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n answer = []\n if not digits:\n return answer\n digit_to_letter = {"2" : "abc",\n "3" : "def",\n "4" : "ghi",\n "5" : "jkl",\n "6" : "mno",\n "7" : "pqrs",\n "8" : "tuv",\n "9" : "wxyz"}\n curr = []\n\n def dfs(idx):\n if idx == len(digits):\n answer.append("".join(curr))\n return\n for letter in digit_to_letter[digits[idx]]:\n curr.append(letter)\n dfs(idx+1)\n curr.pop()\n \n dfs(0)\n return answer\n```\n\n\n# Iterative\n- Time complexity: $$O(n * 4^n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n * 4^n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc letterCombinations(digits string) []string {\n if len(digits) == 0{\n return []string{}\n }\n digit_to_letter := map[string]string{"2" : "abc",\n "3" : "def",\n "4" : "ghi",\n "5" : "jkl",\n "6" : "mno",\n "7" : "pqrs",\n "8" : "tuv",\n "9" : "wxyz"}\n counter := 1\n for _,item := range(digits){\n counter*=len(digit_to_letter[string(item)])\n }\n \n array := make([][]byte, counter)\n \n for _,number := range(digits){\n block := digit_to_letter[string(number)]\n len_block := len(block)\n pos := 0\n counter /= len_block\n repeat := counter\n for i:=0;i<len(array);i++{\n array[i] = append(array[i],block[pos])\n repeat --\n if repeat == 0{\n repeat = counter\n pos++\n pos%=len_block\n }\n }\n }\n \n answer := []string{}\n for _,item := range(array){\n answer = append(answer,string(item))\n }\n return answer\n}\n```\n```python []\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if not digits:\n return []\n \n digit_to_letter = {"2" : "abc",\n "3" : "def",\n "4" : "ghi",\n "5" : "jkl",\n "6" : "mno",\n "7" : "pqrs",\n "8" : "tuv",\n "9" : "wxyz"}\n \n counter = 1\n for item in digits:\n counter*=len(digit_to_letter[item])\n \n answer = [[] for _ in range(counter)]\n \n \n for number in digits:\n block = digit_to_letter[number]\n len_block = len(block)\n pos = 0\n counter //= len_block\n repeat = counter\n for i in range(len(output)):\n answer[i].append(block[pos])\n repeat -= 1\n if repeat == 0:\n repeat = counter\n pos+=1\n pos%=len_block\n \n answer = ["".join(item) for item in answer]\n return answer\n``` | 1 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
✅✅Python Simple Solution 🔥🔥 Easiest🔥 | letter-combinations-of-a-phone-number | 0 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am Giving away my premium content videos related to computer science and data science and also will be sharing well-structured assignments and study materials to clear interviews at top companies to my first 1000 Subscribers. So, **DON\'T FORGET** to Subscribe\n\nhttps://www.youtube.com/@techwired8/?sub_confirmation=1\n```\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if not digits:\n return []\n \n phone = {"2": "abc", "3": "def", "4": "ghi", "5": "jkl", "6": "mno", "7": "pqrs", "8": "tuv", "9": "wxyz"}\n res = []\n \n def backtrack(combination, next_digits):\n if not next_digits:\n res.append(combination)\n return\n \n for letter in phone[next_digits[0]]:\n backtrack(combination + letter, next_digits[1:])\n \n backtrack("", digits)\n return res\n\n```\n**Explanation:**\n\n- We define a helper function "backtrack" that takes two arguments: the current combination and the remaining digits to process.\n\n- If there are no more digits to process, we append the current combination to the final list and return.\n\n- Otherwise, we iterate through each letter that the first remaining digit maps to, and recursively call the "backtrack" function with the new combination and the remaining digits.\n\n- We initialize the final list "res" to an empty list, and call the "backtrack" function with an empty combination and the original phone number.\n\n- Finally, we return the final list of combinations.\n\n\n\n# Please UPVOTE \uD83D\uDC4D | 122 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Simple backtracking : ✅ Java 🔥 | | Python 🔥 | letter-combinations-of-a-phone-number | 1 | 1 | > # Simple backtracking solution : \n\n```java []\nclass Solution {\n public void buildMap(HashMap<Character,String> hmap)\n {\n hmap.put(\'2\',"abc");\n hmap.put(\'3\',"def");\n hmap.put(\'4\',"ghi");\n hmap.put(\'5\',"jkl");\n hmap.put(\'6\',"mno");\n hmap.put(\'7\',"pqrs");\n hmap.put(\'8\',"tuv");\n hmap.put(\'9\',"wxyz");\n }\n public void backtrack(int len,String digits,HashMap<Character,String> hmap,String temp,List<String> result,int idx)\n {\n if(temp.length() == len)\n {\n result.add(new String(temp));\n return;\n }\n for(int i = 0;i<hmap.get(digits.charAt(idx)).length();i++)\n {\n temp = temp+hmap.get(digits.charAt(idx)).charAt(i);\n backtrack(len,digits,hmap,temp,result,idx+1);\n temp = temp.substring(0,temp.length()-1);\n }\n }\n public List<String> letterCombinations(String digits) {\n List<String> result = new ArrayList<>();\n HashMap<Character,String> hmap = new HashMap<>();\n buildMap(hmap);\n if(digits.length() == 0)\n return result;\n backtrack(digits.length(),digits,hmap,"",result,0);\n return result;\n }\n}\n```\n```python []\nclass Solution:\n def build_map(self,hmap):\n hmap[\'2\'] = "abc"\n hmap[\'3\'] = "def"\n hmap[\'4\'] = "ghi"\n hmap[\'5\'] = "jkl"\n hmap[\'6\'] = "mno"\n hmap[\'7\'] = "pqrs"\n hmap[\'8\'] = "tuv"\n hmap[\'9\'] = "wxyz"\n\n def backtrack(self,length, digits, hmap, temp, result, idx):\n if len(temp) == length:\n result.append(temp[:])\n return\n for char in hmap[digits[idx]]:\n temp += char\n self.backtrack(length, digits, hmap, temp, result, idx + 1)\n temp = temp[:-1]\n def letterCombinations(self, digits: str) -> List[str]:\n result = []\n hmap = {}\n self.build_map(hmap)\n if len(digits) == 0:\n return result\n self.backtrack(len(digits), digits, hmap, "", result, 0)\n return result\n```\n> ### *Please don\'t forget to upvote if you\'ve liked my solution.* \u2B06\uFE0F | 3 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
🔥💯Beats 100% 💪 Very Easy C++ || Java || Pyhton3 || Backtracking Detailed Solution 🔥💯 | letter-combinations-of-a-phone-number | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Mapping of Digits to Letters:** The problem is similar to generating all possible combinations of characters you can get from pressing the digits on a telephone keypad. We are given a mapping of each digit to a set of letters.\n\n**Backtracking:** Backtracking is a powerful technique used to explore all possible combinations of a problem space by building a solution incrementally and undoing the choices when they don\'t lead to a valid solution. In this problem, we will use backtracking to generate all possible letter combinations.\n\n**Recursive Exploration:** The basic idea is to consider each digit in the input string and explore all the possible letters associated with that digit. We start with the first digit and try each letter associated with it. Then, for each of these choices, we move on to the next digit and repeat the process.\n\n**Base Case:** We use recursion to handle each digit in the input string one by one. The base case for our recursive function will be when we have processed all the digits in the input string. At this point, we have a valid letter combination, and we can add it to the result list.\n\n**Recursive Call and Backtracking:** For each digit, we loop through all its associated letters and make a recursive call to the function with the next digit. During this recursion, we maintain the current combination of letters. After the recursive call, we remove the last letter added to the combination (backtrack) and try the next letter.\n\n**Combination Generation:** As we go deeper into the recursion, the current combination of letters will build up until we reach the base case. At the base case, we have formed a complete letter combination for the given input. We add this combination to the result list and return to the previous level of the recursion to try other possibilities.\n\nBy using the backtracking approach, we can efficiently generate all possible letter combinations for the given input digits. This approach ensures that we explore all valid combinations by making choices and undoing them when needed, ultimately forming the complete set of combinations.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Create a mapping of digits to letters(Different for different languages). For example:\n```\nmapping = {\n \'2\': \'abc\',\n \'3\': \'def\',\n \'4\': \'ghi\',\n \'5\': \'jkl\',\n \'6\': \'mno\',\n \'7\': \'pqrs\',\n \'8\': \'tuv\',\n \'9\': \'wxyz\'\n}\n```\n2. Initialize an empty list to store the results.\n\n3. Implement a recursive function that takes the current index and a string representing the current combination. Start with index 0 and an empty string.\n\n4. In the recursive function, if the current index is equal to the length of the input digits, add the current combination to the results list and return.\n\n5. Otherwise, get the letters corresponding to the current digit. For each letter, append it to the current combination and make a recursive call with the next index.\n\n6. After the recursive call, remove the last letter added to the current combination (backtrack) and move on to the next letter.\n\n7. Once the recursive function is completed, return the list of results.\n\n# Complexity\n- **Time complexity:** The time complexity of this approach is O(4^n) where n is the number of digits in the input string. This is because each digit can map to up to 4 letters in the worst case, and there are n digits in the input.\n\n- **Space complexity:** The space complexity is O(n) as we are using recursion and the maximum depth of the recursion is n. Additionally, we are using a result list to store the combinations, which can also take up to O(n) space in the worst case.\n\n# Code\n## C++\n```\nclass Solution {\npublic:\n vector<string> letterCombinations(string digits) {\n vector<string> result;\n if (digits.empty()) return result;\n \n unordered_map<char, string> mapping = {\n {\'2\', "abc"},\n {\'3\', "def"},\n {\'4\', "ghi"},\n {\'5\', "jkl"},\n {\'6\', "mno"},\n {\'7\', "pqrs"},\n {\'8\', "tuv"},\n {\'9\', "wxyz"}\n };\n \n string currentCombination;\n backtrack(digits, 0, mapping, currentCombination, result);\n \n return result;\n }\n \n void backtrack(const string& digits, int index, const unordered_map<char, string>& mapping, string& currentCombination, vector<string>& result) {\n if (index == digits.length()) {\n result.push_back(currentCombination);\n return;\n }\n \n char digit = digits[index];\n string letters = mapping.at(digit);\n for (char letter : letters) {\n currentCombination.push_back(letter);\n backtrack(digits, index + 1, mapping, currentCombination, result);\n currentCombination.pop_back(); // Backtrack by removing the last letter added\n }\n }\n};\n```\n## Java\n```\nclass Solution {\n public List<String> letterCombinations(String digits) {\n List<String> result = new ArrayList<>();\n if (digits.isEmpty()) return result;\n \n Map<Character, String> mapping = new HashMap<>();\n mapping.put(\'2\', "abc");\n mapping.put(\'3\', "def");\n mapping.put(\'4\', "ghi");\n mapping.put(\'5\', "jkl");\n mapping.put(\'6\', "mno");\n mapping.put(\'7\', "pqrs");\n mapping.put(\'8\', "tuv");\n mapping.put(\'9\', "wxyz");\n \n StringBuilder currentCombination = new StringBuilder();\n backtrack(digits, 0, mapping, currentCombination, result);\n \n return result;\n }\n \n private void backtrack(String digits, int index, Map<Character, String> mapping, StringBuilder currentCombination, List<String> result) {\n if (index == digits.length()) {\n result.add(currentCombination.toString());\n return;\n }\n \n char digit = digits.charAt(index);\n String letters = mapping.get(digit);\n for (char letter : letters.toCharArray()) {\n currentCombination.append(letter);\n backtrack(digits, index + 1, mapping, currentCombination, result);\n currentCombination.deleteCharAt(currentCombination.length() - 1); // Backtrack by removing the last letter added\n }\n }\n}\n\n```\n## Pyhton3\n```\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n result = []\n if not digits:\n return result\n \n mapping = {\n \'2\': \'abc\',\n \'3\': \'def\',\n \'4\': \'ghi\',\n \'5\': \'jkl\',\n \'6\': \'mno\',\n \'7\': \'pqrs\',\n \'8\': \'tuv\',\n \'9\': \'wxyz\'\n }\n \n def backtrack(index, current_combination):\n nonlocal result\n if index == len(digits):\n result.append(current_combination)\n return\n \n digit = digits[index]\n letters = mapping[digit]\n for letter in letters:\n backtrack(index + 1, current_combination + letter)\n \n backtrack(0, "")\n return result\n\n```\n\n | 33 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Python 1-liner. Functional programming. | letter-combinations-of-a-phone-number | 0 | 1 | # Complexity\n- Time complexity: $$O(4^n)$$\n\n- Space complexity: $$O(4^n)$$, including output space.\n\nwhere, `n is length of digits`.\n\n# Code\n```python\nclass Solution:\n def letterCombinations(self, digits: str) -> list[str]:\n phone = {\n \'1\': \'\' , \'2\': \'abc\', \'3\': \'def\',\n \'4\': \'ghi\' , \'5\': \'jkl\', \'6\': \'mno\',\n \'7\': \'pqrs\', \'8\': \'tuv\', \'9\': \'wxyz\'\n }\n\n return list(map(\'\'.join, product(*map(phone.get, digits)))) if digits else []\n\n\n``` | 1 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Hey Knight! You need to see this! | letter-combinations-of-a-phone-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if not digits:\n return []\n L=[]\n map = {"2":"abc","3":"def","4":"ghi","5":"jkl","6":"mno","7":"pqrs","8":"tuv","9":"wxyz"}\n\n def com(combination,digit):\n if not digit:\n return L.append(combination)\n \n digit_str=map[digit[0]]\n for letter in digit_str:\n com(combination+letter,digit[1:])\n return L\n return com("",digits)\n \n\n \n\n``` | 2 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | letter-combinations-of-a-phone-number | 1 | 1 | # Intuition\nUsing backtracking to create all possible combinations\n\n---\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/q0RJHpE92Zk\n\n# Subscribe to my channel from here. I have 239 videos as of August 3rd\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n\n# Approach\nThis is based on Python solution. Other might be differnt a bit.\n\n1. Initialize an empty list `res` to store the generated combinations.\n\n2. Check if the `digits` string is empty. If it is, return an empty list since there are no digits to process.\n\n3. Create a dictionary `digit_to_letters` that maps each digit from \'2\' to \'9\' to the corresponding letters on a phone keypad.\n\n4. Define a recursive function `backtrack(idx, comb)` that takes two parameters:\n - `idx`: The current index of the digit being processed in the `digits` string.\n - `comb`: The current combination being formed by appending letters.\n\n5. Inside the `backtrack` function:\n - Check if `idx` is equal to the length of the `digits` string. If it is, it means a valid combination has been formed, so append the current `comb` to the `res` list.\n - If not, iterate through each letter corresponding to the digit at `digits[idx]` using the `digit_to_letters` dictionary.\n - For each letter, recursively call `backtrack` with `idx + 1` to process the next digit and `comb + letter` to add the current letter to the combination.\n\n6. Initialize the `res` list.\n\n7. Start the initial call to `backtrack` with `idx` set to 0 and an empty string as `comb`. This will start the process of generating combinations.\n\n8. After the recursive calls have been made, return the `res` list containing all the generated combinations.\n\nThe algorithm works by iteratively exploring all possible combinations of letters that can be formed from the given input digits. It uses a recursive approach to generate combinations, building them one letter at a time. The base case for the recursion is when all digits have been processed, at which point a combination is complete and added to the `res` list. The backtracking nature of the algorithm ensures that all possible combinations are explored.\n\n# Complexity\n- Time complexity: O(3^n) or O(4^n)\nn is length of input string. Each digit has 3 or 4 letters. For example, if you get "23"(n) as input string, we will create 9 combinations which is O(3^2) = 9\n\n- Space complexity: O(n)\nn is length of input string. This is for recursive call stack.\n\n```python []\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if not digits:\n return []\n \n digit_to_letters = {\n \'2\': \'abc\',\n \'3\': \'def\',\n \'4\': \'ghi\',\n \'5\': \'jkl\',\n \'6\': \'mno\',\n \'7\': \'pqrs\',\n \'8\': \'tuv\',\n \'9\': \'wxyz\',\n }\n\n def backtrack(idx, comb):\n if idx == len(digits):\n res.append(comb[:])\n return\n \n for letter in digit_to_letters[digits[idx]]:\n backtrack(idx + 1, comb + letter)\n\n res = []\n backtrack(0, "")\n\n return res\n```\n```javascript []\n/**\n * @param {string} digits\n * @return {string[]}\n */\nvar letterCombinations = function(digits) {\n if (!digits.length) {\n return [];\n }\n \n const digitToLetters = {\n \'2\': \'abc\',\n \'3\': \'def\',\n \'4\': \'ghi\',\n \'5\': \'jkl\',\n \'6\': \'mno\',\n \'7\': \'pqrs\',\n \'8\': \'tuv\',\n \'9\': \'wxyz\'\n };\n \n const res = [];\n \n function backtrack(idx, comb) {\n if (idx === digits.length) {\n res.push(comb);\n return;\n }\n \n for (const letter of digitToLetters[digits[idx]]) {\n backtrack(idx + 1, comb + letter);\n }\n }\n \n backtrack(0, "");\n \n return res; \n};\n```\n```Java []\nclass Solution {\n public List<String> letterCombinations(String digits) {\n List<String> res = new ArrayList<>();\n \n if (digits == null || digits.length() == 0) {\n return res;\n }\n \n Map<Character, String> digitToLetters = new HashMap<>();\n digitToLetters.put(\'2\', "abc");\n digitToLetters.put(\'3\', "def");\n digitToLetters.put(\'4\', "ghi");\n digitToLetters.put(\'5\', "jkl");\n digitToLetters.put(\'6\', "mno");\n digitToLetters.put(\'7\', "pqrs");\n digitToLetters.put(\'8\', "tuv");\n digitToLetters.put(\'9\', "wxyz");\n \n backtrack(digits, 0, new StringBuilder(), res, digitToLetters);\n \n return res; \n }\n\n private void backtrack(String digits, int idx, StringBuilder comb, List<String> res, Map<Character, String> digitToLetters) {\n if (idx == digits.length()) {\n res.add(comb.toString());\n return;\n }\n \n String letters = digitToLetters.get(digits.charAt(idx));\n for (char letter : letters.toCharArray()) {\n comb.append(letter);\n backtrack(digits, idx + 1, comb, res, digitToLetters);\n comb.deleteCharAt(comb.length() - 1);\n }\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<string> letterCombinations(string digits) {\n vector<string> res;\n \n if (digits.empty()) {\n return res;\n }\n \n unordered_map<char, string> digitToLetters = {\n {\'2\', "abc"},\n {\'3\', "def"},\n {\'4\', "ghi"},\n {\'5\', "jkl"},\n {\'6\', "mno"},\n {\'7\', "pqrs"},\n {\'8\', "tuv"},\n {\'9\', "wxyz"}\n };\n \n backtrack(digits, 0, "", res, digitToLetters);\n \n return res; \n }\n\n void backtrack(const string& digits, int idx, string comb, vector<string>& res, const unordered_map<char, string>& digitToLetters) {\n if (idx == digits.length()) {\n res.push_back(comb);\n return;\n }\n \n string letters = digitToLetters.at(digits[idx]);\n for (char letter : letters) {\n backtrack(digits, idx + 1, comb + letter, res, digitToLetters);\n }\n } \n};\n```\n | 19 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
🚀 One-Liner Solution to Letter Combinations of a Phone Number | letter-combinations-of-a-phone-number | 0 | 1 | # Intuition\nGiven a string containing digits from 2-9 inclusive, we need to return all possible letter combinations that the number could represent. This can be achieved using a compact one-liner code that leverages Python\'s list comprehension and the itertools module.\n\n# Approach\n1. **Create Mapping**: Use list comprehension to map each digit to its corresponding letters (e.g., \'2\' maps to "abc," \'3\' maps to "def," etc.).\n2. **Generate Combinations**: Utilize the `product` function from the `itertools` module to generate all possible combinations of these letters.\n3. **Convert to Strings**: Iterate through the combinations, join each into a string, and return as a list.\n\n# Complexity\n- Time complexity: \\(O(4^n)\\), where \\(n\\) is the length of the input string. In the worst case, each digit can represent 4 letters.\n- Space complexity: \\(O(n)\\), where \\(n\\) is the length of the input string.\n\n# Code\n```python\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n return list("".join(c) for c in product(*[[chr(ord(\'a\') + (ord(d) - ord(\'2\')) * 3 + i) for i in range(0 + (d > \'7\'), 3 + (d > \'6\') + (d == \'9\'))] for d in digits]) if c)\n```\n\nThis one-liner code offers a compact and efficient solution to the problem, cleverly utilizing Python\'s powerful list comprehension and itertools features. It\'s a great example of how expressive and concise Python code can be! | 4 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
3 Approaches || Faster than 99% | letter-combinations-of-a-phone-number | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(n* 4^N)\n\n- Space complexity:\nO(4^N)\n\n\n```python1st []\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n res = []\n digitTochar= {"2": "abc", \n "3": "def",\n "4": "ghi",\n "5": "jkl",\n "6": "mno",\n "7": "pqrs",\n "8": "tuv",\n "9": "wxyz"\n }\n\n def backtrack (i,crr): \n if len(crr)== len(digits): \n res.append(crr)\n return \n\n for c in digitTochar[digits[i]]: \n backtrack(i+1 , crr + c)\n\n if digits : \n backtrack(0,"")\n return res \n return []\n\n```\n```python2nd []\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if len(digits) == 0:\n return []\n \n digitTochar= {"2": "abc", \n "3": "def",\n "4": "ghi",\n "5": "jkl",\n "6": "mno",\n "7": "pqrs",\n "8": "tuv",\n "9": "wxyz"\n }\n\n output=[""]\n for d in digits:\n tmp=[]\n for c in digitTochar[d]:\n for o in output:\n tmp.append(o+c)\n output=tmp\n return output\n```\n```python3rd []\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if len(digits) == 0:\n return []\n \n digitTochar= {"2": ["a", "b", "c"], \n "3": ["d", "e", "f"],\n "4": ["g", "h", "i"],\n "5": ["j", "k", "l"],\n "6": ["m", "n", "o"],\n "7": ["p", "q", "r", "s"],\n "8": ["t", "u", "v"],\n "9": ["w", "x", "y", "z"]\n }\n \n if len(digits) == 1:\n return digitTochar[digits]\n \n res = []\n for i in digitTochar[digits[0]]:\n for j in digitTochar[digits[1]]:\n if len(digits) == 2:\n res.append(i + j)\n else:\n for k in digitTochar[digits[2]]:\n if len(digits) == 3:\n res.append(i + j + k)\n else:\n for l in digitTochar[digits[3]]:\n res.append(i+j+k+l) \n return res\n```\n\n | 1 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Simple python solution using Dqueue and dictionary which beats 88% | letter-combinations-of-a-phone-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def letterCombinations(self, digits: str) -> List[str]:\n if not digits:\n return []\n\n d_letters = {\n \'2\': \'abc\',\n \'3\': \'def\',\n \'4\': \'ghi\',\n \'5\': \'jkl\',\n \'6\': \'mno\',\n \'7\': \'pqrs\',\n \'8\': \'tuv\',\n \'9\': \'wxyz\'\n }\n queue = deque(d_letters[digits[0]])\n\n \n for digit in digits[1:]:\n \n letters = d_letters[digit]\n current_length = len(queue)\n for _ in range(current_length):\n combination = queue.popleft()\n for letter in letters:\n queue.append(combination + letter)\n\n return list(queue)\n\n \n\n``` | 1 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
**Example 1:**
**Input:** digits = "23 "
**Output:** \[ "ad ", "ae ", "af ", "bd ", "be ", "bf ", "cd ", "ce ", "cf "\]
**Example 2:**
**Input:** digits = " "
**Output:** \[\]
**Example 3:**
**Input:** digits = "2 "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `0 <= digits.length <= 4`
* `digits[i]` is a digit in the range `['2', '9']`. | null |
Sum MegaPost - Python3 Solution with a detailed explanation | 4sum | 0 | 1 | If you\'re a newbie and sometimes have a hard time understanding the logic. Don\'t worry, you\'ll catch up after a month of doing Leetcode on a daily basis. Try to do it, even one example per day. It\'d help. I\'ve compiled a bunch on `sum` problems here, go ahead and check it out. Also, I think focusing on a subject and do 3-4 problems would help to get the idea behind solution since they mostly follow the same logic. Of course there are other ways to solve each problems but I try to be as uniform as possible. Good luck. \n\nIn general, `sum` problems can be categorized into two categories: 1) there is any array and you add some numbers to get to (or close to) a `target`, or 2) you need to return indices of numbers that sum up to a (or close to) a `target` value. Note that when the problem is looking for a indices, `sort`ing the array is probably NOT a good idea. \n\n\n **[Two Sum:](https://leetcode.com/problems/two-sum/)** \n \n This is the second type of the problems where we\'re looking for indices, so sorting is not necessary. What you\'d want to do is to go over the array, and try to find two integers that sum up to a `target` value. Most of the times, in such a problem, using dictionary (hastable) helps. You try to keep track of you\'ve observations in a dictionary and use it once you get to the results. \n\nNote: try to be comfortable to use `enumerate` as it\'s sometime out of comfort zone for newbies. `enumerate` comes handy in a lot of problems (I mean if you want to have a cleaner code of course). If I had to choose three built in functions/methods that I wasn\'t comfortable with at the start and have found them super helpful, I\'d probably say `enumerate`, `zip` and `set`. \n \nSolution: In this problem, you initialize a dictionary (`seen`). This dictionary will keep track of numbers (as `key`) and indices (as `value`). So, you go over your array (line `#1`) using `enumerate` that gives you both index and value of elements in array. As an example, let\'s do `nums = [2,3,1]` and `target = 3`. Let\'s say you\'re at index `i = 0` and `value = 2`, ok? you need to find `value = 1` to finish the problem, meaning, `target - 2 = 1`. 1 here is the `remaining`. Since `remaining + value = target`, you\'re done once you found it, right? So when going through the array, you calculate the `remaining` and check to see whether `remaining` is in the `seen` dictionary (line `#3`). If it is, you\'re done! you\'re current number and the remaining from `seen` would give you the output (line `#4`). Otherwise, you add your current number to the dictionary (line `#5`) since it\'s going to be a `remaining` for (probably) a number you\'ll see in the future assuming that there is at least one instance of answer. \n \n \n ```\n class Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n seen = {}\n for i, value in enumerate(nums): #1\n remaining = target - nums[i] #2\n \n if remaining in seen: #3\n return [i, seen[remaining]] #4\n else:\n seen[value] = i #5\n```\n \n \n\n **[Two Sum II:](https://leetcode.com/problems/two-sum-ii-input-array-is-sorted/)** \n\nFor this, you can do exactly as the previous. The only change I made below was to change the order of line `#4`. In the previous example, the order didn\'t matter. But, here the problem asks for asending order and since the values/indicess in `seen` has always lower indices than your current number, it should come first. Also, note that the problem says it\'s not zero based, meaning that indices don\'t start from zero, that\'s why I added 1 to both of them. \n\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n \n seen = {}\n for i, value in enumerate(numbers): \n remaining = target - numbers[i] \n \n if remaining in seen: \n return [seen[remaining]+1, i+1] #4\n else:\n seen[value] = i \n```\n\nAnother approach to solve this problem (probably what Leetcode is looking for) is to treat it as first category of problems. Since the array is already sorted, this works. You see the following approach in a lot of problems. What you want to do is to have two pointer (if it was 3sum, you\'d need three pointers as you\'ll see in the future examples). One pointer move from `left` and one from `right`. Let\'s say you `numbers = [1,3,6,9]` and your `target = 10`. Now, `left` points to 1 at first, and `right` points to 9. There are three possibilities. If you sum numbers that `left` and `right` are pointing at, you get `temp_sum` (line `#1`). If `temp_sum` is your target, you\'r done! You\'re return it (line `#9`). If it\'s more than your `target`, it means that `right` is poiting to a very large value (line `#5`) and you need to bring it a little bit to the left to a smaller (r maybe equal) value (line `#6`) by adding one to the index . If the `temp_sum` is less than `target` (line `#7`), then you need to move your `left` to a little bit larger value by adding one to the index (line `#9`). This way, you try to narrow down the range in which you\'re looking at and will eventually find a couple of number that sum to `target`, then, you\'ll return this in line `#9`. In this problem, since it says there is only one solution, nothing extra is necessary. However, when a problem asks to return all combinations that sum to `target`, you can\'t simply return the first instace and you need to collect all the possibilities and return the list altogether (you\'ll see something like this in the next example). \n\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n \n for left in range(len(numbers) -1): #1\n right = len(numbers) - 1 #2\n while left < right: #3\n temp_sum = numbers[left] + numbers[right] #4\n if temp_sum > target: #5\n right -= 1 #6\n elif temp_sum < target: #7\n left +=1 #8\n else:\n return [left+1, right+1] #9\n```\n\n\n\n\n[**3Sum**](https://leetcode.com/problems/3sum/)\n\nThis is similar to the previous example except that it\'s looking for three numbers. There are some minor differences in the problem statement. It\'s looking for all combinations (not just one) of solutions returned as a list. And second, it\'s looking for unique combination, repeatation is not allowed. \n\nHere, instead of looping (line `#1`) to `len(nums) -1`, we loop to `len(nums) -2` since we\'re looking for three numbers. Since we\'re returning values, `sort` would be a good idea. Otherwise, if the `nums` is not sorted, you cannot reducing `right` pointer or increasing `left` pointer easily, makes sense? \n\nSo, first you `sort` the array and define `res = []` to collect your outputs. In line `#2`, we check wether two consecutive elements are equal or not because if they are, we don\'t want them (solutions need to be unique) and will skip to the next set of numbers. Also, there is an additional constrain in this line that `i > 0`. This is added to take care of cases like `nums = [1,1,1]` and `target = 3`. If we didn\'t have `i > 0`, then we\'d skip the only correct solution and would return `[]` as our answer which is wrong (correct answer is `[[1,1,1]]`. \n\nWe define two additional pointers this time, `left = i + 1` and `right = len(nums) - 1`. For example, if `nums = [-2,-1,0,1,2]`, all the points in the case of `i=1` are looking at: `i` at `-1`, `left` at `0` and `right` at `2`. We then check `temp` variable similar to the previous example. There is only one change with respect to the previous example here between lines `#5` and `#10`. If we have the `temp = target`, we obviously add this set to the `res` in line `#5`, right? However, we\'re not done yet. For a fixed `i`, we still need to check and see whether there are other combinations by just changing `left` and `right` pointers. That\'s what we are doing in lines `#6, 7, 8`. If we still have the condition of `left < right` and `nums[left]` and the number to the right of it are not the same, we move `left` one index to right (line `#6`). Similarly, if `nums[right]` and the value to left of it is not the same, we move `right` one index to left. This way for a fixed `i`, we get rid of repeative cases. For example, if `nums = [-3, 1,1, 3,5]` and `target = 3`, one we get the first `[-3,1,5]`, `left = 1`, but, `nums[2]` is also 1 which we don\'t want the `left` variable to look at it simply because it\'d again return `[-3,1,5]`, right? So, we move `left` one index. Finally, if the repeating elements don\'t exists, lines `#6` to `#8` won\'t get activated. In this case we still need to move forward by adding 1 to `left` and extracting 1 from `right` (lines `#9, 10`). \n\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n \n nums.sort()\n res = []\n\n for i in range(len(nums) -2): #1\n if i > 0 and nums[i] == nums[i-1]: #2\n continue\n left = i + 1 #3\n right = len(nums) - 1 #4\n \n while left < right: \n temp = nums[i] + nums[left] + nums[right]\n \n if temp > 0:\n right -= 1\n \n elif temp < 0:\n left += 1\n \n else:\n res.append([nums[i], nums[left], nums[right]]) #5\n while left < right and nums[left] == nums[left + 1]: #6\n left += 1\n while left < right and nums[right] == nums[right-1]:#7\n right -= 1 #8\n \n right -= 1 #9 \n left += 1 #10\n \n```\n\nAnother way to solve this problem is to change it into a two sum problem. Instead of finding `a+b+c = 0`, you can find `a+b = -c` where we want to find two numbers `a` and `b` that are equal to `-c`, right? This is similar to the first problem. Remember if you wanted to use the exact same as the first code, it\'d return indices and not numbers. Also, we need to re-arrage this problem in a way that we have `nums` and `target`. This code is not a good code and can be optimipized but you got the idea. For a better version of this, check [this](https://leetcode.com/problems/3sum/discuss/7384/My-Python-solution-based-on-2-sum-200-ms-beat-93.37). \n\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n res = []\n nums.sort()\n \n for i in range(len(nums)-2):\n if i > 0 and nums[i] == nums[i-1]:\n continue\n output_2sum = self.twoSum(nums[i+1:], -nums[i])\n if output_2sum ==[]:\n continue\n else:\n for idx in output_2sum:\n instance = idx+[nums[i]]\n res.append(instance)\n \n output = []\n for idx in res:\n if idx not in output:\n output.append(idx)\n \n \n return output\n \n \n def twoSum(self, nums, target):\n seen = {}\n res = []\n for i, value in enumerate(nums): #1\n remaining = target - nums[i] #2\n \n if remaining in seen: #3\n res.append([value, remaining]) #4\n else:\n seen[value] = i #5\n \n return res\n```\n\n[**4Sum**](https://leetcode.com/problems/4sum/)\n\nYou should have gotten the idea, and what you\'ve seen so far can be generalized to `nSum`. Here, I write the generic code using the same ideas as before. What I\'ll do is to break down each case to a `2Sum II` problem, and solve them recursively using the approach in `2Sum II` example above. \n\nFirst sort `nums`, then I\'m using two extra functions, `helper` and `twoSum`. The `twoSum` is similar to the `2sum II` example with some modifications. It doesn\'t return the first instance of results, it check every possible combinations and return all of them now. Basically, now it\'s more similar to the `3Sum` solution. Understanding this function shouldn\'t be difficult as it\'s very similar to `3Sum`. As for `helper` function, it first tries to check for cases that don\'t work (line `#1`). And later, if the `N` we need to sum to get to a `target` is 2 (line `#2`), then runs the `twoSum` function. For the more than two numbers, it recursively breaks them down to two sum (line `#3`). There are some cases like line `#4` that we don\'t need to proceed with the algorithm anymore and we can `break`. These cases include if multiplying the lowest number in the list by `N` is more than `target`. Since its sorted array, if this happens, we can\'t find any result. Also, if the largest array (`nums[-1]`) multiplied by `N` would be less than `target`, we can\'t find any solution. So, `break`. \n\n\nFor other cases, we run the `helper` function again with new inputs, and we keep doing it until we get to `N=2` in which we use `twoSum` function, and add the results to get the final output. \n\n```\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n nums.sort()\n results = []\n self.helper(nums, target, 4, [], results)\n return results\n \n def helper(self, nums, target, N, res, results):\n \n if len(nums) < N or N < 2: #1\n return\n if N == 2: #2\n output_2sum = self.twoSum(nums, target)\n if output_2sum != []:\n for idx in output_2sum:\n results.append(res + idx)\n \n else: \n for i in range(len(nums) -N +1): #3\n if nums[i]*N > target or nums[-1]*N < target: #4\n break\n if i == 0 or i > 0 and nums[i-1] != nums[i]: #5\n self.helper(nums[i+1:], target-nums[i], N-1, res + [nums[i]], results)\n \n \n def twoSum(self, nums: List[int], target: int) -> List[int]:\n res = []\n left = 0\n right = len(nums) - 1 \n while left < right: \n temp_sum = nums[left] + nums[right] \n\n if temp_sum == target:\n res.append([nums[left], nums[right]])\n right -= 1\n left += 1\n while left < right and nums[left] == nums[left - 1]:\n left += 1\n while right > left and nums[right] == nums[right + 1]:\n right -= 1\n \n elif temp_sum < target: \n left +=1 \n else: \n right -= 1\n \n return res\n```\n\n[**Combination Sum II**](https://leetcode.com/problems/combination-sum-ii/)\nI don\'t post combination sum here since it\'s basically this problem a little bit easier. \nCombination questions can be solved with `dfs` most of the time. if you want to fully understand this concept and [backtracking](https://www.***.org/backtracking-introduction/), try to finish [this](https://leetcode.com/problems/combination-sum/discuss/429538/General-Backtracking-questions-solutions-in-Python-for-reference-%3A) post and do all the examples. \n\nRead my older post first [here](https://leetcode.com/problems/combinations/discuss/729397/python3-solution-with-detailed-explanation). This should give you a better idea of what\'s going on. The solution here also follow the exact same format except for some minor changes. I first made a minor change in the `dfs` function where it doesn\'t need the `index` parameter anymore. This is taken care of by `candidates[i+1:]` in line `#3`. Note that we had `candidates` here in the previous post. \n\n```\nclass Solution(object):\n def combinationSum2(self, candidates, target):\n """\n :type candidates: List[int]\n :type target: int\n :rtype: List[List[int]]\n """\n res = []\n candidates.sort()\n self.dfs(candidates, target, [], res)\n return res\n \n \n def dfs(self, candidates, target, path, res):\n if target < 0:\n return\n \n if target == 0:\n res.append(path)\n return res\n \n for i in range(len(candidates)):\n if i > 0 and candidates[i] == candidates[i-1]: #1\n continue #2\n self.dfs(candidates[i+1:], target - candidates[i], path+[candidates[i]], res) #3\n```\n\n\nThe only differences are lines `#1, 2, 3`. The difference in problem statement in this one and `combinations` problem of my previous post is >>>candidates must be used once<<< and lines `#1` and `2` are here to take care of this. Line `#1` has two components where first `i > 0` and second `candidates[i] == candidates[i-1]`. The second component `candidates[i] == candidates[i-1]` is to take care of duplicates in the `candidates` variable as was instructed in the problem statement. Basically, if the next number in `candidates` is the same as the previous one, it means that it has already been taken care of, so `continue`. The first component takes care of cases like an input `candidates = [1]` with `target = 1` (try to remove this component and submit your solution. You\'ll see what I mean). The rest is similar to the previous [post](https://leetcode.com/problems/combinations/discuss/729397/python3-solution-with-detailed-explanation)\n\n\n\n================================================================\nFinal note: Please let me know if you found any typo/error/ect. I\'ll try to fix them. | 146 | Given an array `nums` of `n` integers, return _an array of all the **unique** quadruplets_ `[nums[a], nums[b], nums[c], nums[d]]` such that:
* `0 <= a, b, c, d < n`
* `a`, `b`, `c`, and `d` are **distinct**.
* `nums[a] + nums[b] + nums[c] + nums[d] == target`
You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,0,-1,0,-2,2\], target = 0
**Output:** \[\[-2,-1,1,2\],\[-2,0,0,2\],\[-1,0,0,1\]\]
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], target = 8
**Output:** \[\[2,2,2,2\]\]
**Constraints:**
* `1 <= nums.length <= 200`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109` | null |
Python3 | Brute-force > Better > Optimal | Full Explanation | 4sum | 0 | 1 | - Approach\n - Brute-force\n - We keep four-pointers `i`, `j`, `k` and `l`. For every quadruplet, we find the sum of `A[i]+A[j]+A[k]+A[l]`\n - If this sum equals the target, we\u2019ve found one of the quadruplets and add it to our data structure and continue with the rest\n - Time Complexity: $O(n^4)$\n - Space Complexity: $O(m)$ where m is the number of quadruplets\n - Better\n - We store the frequency of each element in a HashMap\n - Based on `a + b + c + d = target` we can say that `d = target - (a+b+c)` and based on this we fix 3 elements `a`, `b` and `c` and try to find the `-(a+b+c)` in HashMap\n - Time Complexity: $O(n^3)$\n - Space Complexity: $O(n + m)$ where m is the number of quadruplets\n - Optimal\n - To get the quadruplets in sorted order, we will sort the entire array in the first step and to get the unique quads, we will simply skip the duplicate numbers while moving the pointers\n - Fix 2 pointers `i` and `j` and move 2 pointers `lo` and `hi`\n - Based on `a + b + c + d = target` we can say that `c + d = target - (a+b)` and based on this we fix element as `a` and `b` then find `c` and `d` using two pointers `lo` and `hi` (same as in 3Sum Problem)\n - Time Complexity: $O(n^3)$\n - Space Complexity: $O(m)$ where m is the number of quadruplets\n\n```python\n# Python3\n# Brute-force Solution\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n n = len(nums)\n ans = set()\n for i in range(n-3):\n for j in range(i+1, n-2):\n for k in range(j+1, n-1):\n for l in range(k+1, n):\n if nums[i] + nums[j] + nums[k] + nums[l] == target:\n ans.add(tuple(sorted((nums[i], nums[j], nums[k], nums[l]))))\n \n res = []\n for i in ans:\n res += list(i),\n return res\n```\n\n```python\n# Python3\n# Better Solution\nfrom collections import defaultdict\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n n = len(nums)\n ans = set()\n hmap = defaultdict(int)\n for i in nums:\n hmap[i] += 1\n \n for i in range(n-3):\n hmap[nums[i]] -= 1\n for j in range(i+1, n-2):\n hmap[nums[j]] -= 1\n for k in range(j+1, n-1):\n hmap[nums[k]] -= 1\n rem = target-(nums[i] + nums[j] + nums[k])\n if rem in hmap and hmap[rem] > 0:\n ans.add(tuple(sorted((nums[i], nums[j], nums[k], rem))))\n hmap[nums[k]] += 1\n hmap[nums[j]] += 1\n hmap[nums[i]] += 1\n \n res = []\n for i in ans:\n res += list(i),\n return res\n```\n\n```python\n# Python3\n# Optimal Solution\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n n = len(nums)\n nums.sort()\n res = []\n\n for i in range(n-3):\n # avoid the duplicates while moving i\n if i > 0 and nums[i] == nums[i - 1]:\n continue\n for j in range(i+1, n-2):\n # avoid the duplicates while moving j\n if j > i + 1 and nums[j] == nums[j - 1]:\n continue\n lo = j + 1\n hi = n - 1\n while lo < hi:\n temp = nums[i] + nums[j] + nums[lo] + nums[hi]\n if temp == target:\n res += [nums[i], nums[j], nums[lo], nums[hi]],\n\n # skip duplicates\n while lo < hi and nums[lo] == nums[lo + 1]:\n lo += 1\n lo += 1\n while lo < hi and nums[hi] == nums[hi - 1]:\n hi -= 1\n hi -= 1\n elif temp < target:\n lo += 1\n else:\n hi -= 1\n return res\n``` | 7 | Given an array `nums` of `n` integers, return _an array of all the **unique** quadruplets_ `[nums[a], nums[b], nums[c], nums[d]]` such that:
* `0 <= a, b, c, d < n`
* `a`, `b`, `c`, and `d` are **distinct**.
* `nums[a] + nums[b] + nums[c] + nums[d] == target`
You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[1,0,-1,0,-2,2\], target = 0
**Output:** \[\[-2,-1,1,2\],\[-2,0,0,2\],\[-1,0,0,1\]\]
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], target = 8
**Output:** \[\[2,2,2,2\]\]
**Constraints:**
* `1 <= nums.length <= 200`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109` | null |
Python3 if and while case solution | remove-nth-node-from-end-of-list | 0 | 1 | # Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:\n sayac = 0\n temp = head\n if temp.next == None: \n return None \n while temp != None:\n temp = temp.next\n sayac = sayac + 1\n temp = head\n if sayac - n == 0:\n temp = head.next\n while temp != None: \n return temp\n for num in range(sayac-n-1): \n temp = temp.next\n temp.next = temp.next.next\n temp = head\n return temp\n \n``` | 1 | Given the `head` of a linked list, remove the `nth` node from the end of the list and return its head.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], n = 2
**Output:** \[1,2,3,5\]
**Example 2:**
**Input:** head = \[1\], n = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[1,2\], n = 1
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is `sz`.
* `1 <= sz <= 30`
* `0 <= Node.val <= 100`
* `1 <= n <= sz`
**Follow up:** Could you do this in one pass? | Maintain two pointers and update one with a delay of n steps. |
Python Two Pointer solution with comments Easy to Understand | remove-nth-node-from-end-of-list | 0 | 1 | Please upvote once you get this :)\n```\nclass Solution:\n def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:\n fast = head\n slow = head\n # advance fast to nth position\n for i in range(n):\n fast = fast.next\n \n if not fast:\n return head.next\n # then advance both fast and slow now they are nth postions apart\n # when fast gets to None, slow will be just before the item to be deleted\n while fast.next:\n slow = slow.next\n fast = fast.next\n # delete the node\n slow.next = slow.next.next\n return head\n``` | 187 | Given the `head` of a linked list, remove the `nth` node from the end of the list and return its head.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], n = 2
**Output:** \[1,2,3,5\]
**Example 2:**
**Input:** head = \[1\], n = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[1,2\], n = 1
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is `sz`.
* `1 <= sz <= 30`
* `0 <= Node.val <= 100`
* `1 <= n <= sz`
**Follow up:** Could you do this in one pass? | Maintain two pointers and update one with a delay of n steps. |
Beats 100%✅ | O( n )✅ | Easy-To-Understand✅ | Python (Step by step explanation)✅ | remove-nth-node-from-end-of-list | 0 | 1 | # Intuition\nTo remove the nth node from the end of a singly-linked list, we can calculate the length of the list, and then identify the target node to be removed. It\'s important to handle edge cases where `n` is equal to the length of the list or when the list contains only one node.\n\n# Approach\n1. Initialize `temp` as the head of the linked list and `count` as 0 to keep track of the number of nodes.\n2. Traverse the linked list using `temp` and increment `count` for each node visited.\n3. Check if `count` is equal to 1. If it is, this means the list contains only one node, so return `None` to indicate an empty list.\n4. Reset `temp` to the head of the list and update `count` to be `count - n + 1`. This step calculates the position of the node to be removed.\n5. If `count` is now 1, we want to remove the head of the list, so return `head.next` to indicate the new head.\n6. Otherwise, traverse the list again while decrementing `count` by 2 each time, stopping just before the target node.\n7. If `n` is equal to 1, set `temp.next` to `None` to remove the last node.\n8. Otherwise, update `temp.next` to skip the target node and connect to the next node.\n9. Finally, return `head`, which is the updated linked list with the nth node from the end removed.\n\n# Complexity\n- Time complexity: O(n) where n is the number of nodes in the linked list.\n- Space complexity: O(1) since we use a constant amount of extra space for variables.\n\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:\n temp = head\n count = 0\n while temp:\n count +=1\n temp = temp.next\n\n if count == 1:\n return None \n \n temp = head\n count = count - n +1\n\n if count == 1 :\n return head.next\n\n\n while (count -2 ):\n \n temp = temp.next\n count -= 1\n \n if n == 1:\n temp.next = None\n else:\n temp.next = temp.next.next \n\n return head\n\n\n\n \n```\n\n# Please upvote the solution if you understood it.\n\n | 1 | Given the `head` of a linked list, remove the `nth` node from the end of the list and return its head.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], n = 2
**Output:** \[1,2,3,5\]
**Example 2:**
**Input:** head = \[1\], n = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[1,2\], n = 1
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is `sz`.
* `1 <= sz <= 30`
* `0 <= Node.val <= 100`
* `1 <= n <= sz`
**Follow up:** Could you do this in one pass? | Maintain two pointers and update one with a delay of n steps. |
Beats 100%✅ | O( n )✅ | Easy-To-Understand✅ | Python (Step by step explanation)✅ | remove-nth-node-from-end-of-list | 0 | 1 | # Intuition\nThe intuition for solving this problem is to use two pointers, `l` and `r`, to create a "window" of size `n` between them. This "window" will help us identify the nth node from the end of the linked list. \n\n# Approach\n1. Initialize `temp` as a new ListNode with a value of 0 and `head` as its next node. This `temp` node serves as a dummy node to handle edge cases where the target node is the head of the list.\n2. Initialize two pointers, `l` and `r`, both initially pointing to `temp`. Move `r` `n` nodes ahead to create a "window" of size `n` between `l` and `r`.\n3. Traverse the linked list by moving `l` and `r` one node at a time until `r` reaches the end of the list.\n4. At this point, `l` is pointing to the node just before the target node. Update `l.next` to skip the target node and connect to the node after it.\n5. Return `temp.next`, which is the head of the updated linked list.\n\n# Complexity\n- Time complexity: O(n), where n is the number of nodes in the linked list.\n- Space complexity: O(1), as we use a constant amount of extra space for variables.\n\n\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:\n temp = ListNode(0, head)\n l = temp\n r = head\n\n while n > 0:\n r = r.next\n n -= 1\n\n while r:\n l = l.next\n r = r.next\n\n \n l.next = l.next.next\n return temp.next\n\n\n \n```\n\n# Please upvote the solution if you understood it.\n\n | 3 | Given the `head` of a linked list, remove the `nth` node from the end of the list and return its head.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], n = 2
**Output:** \[1,2,3,5\]
**Example 2:**
**Input:** head = \[1\], n = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[1,2\], n = 1
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is `sz`.
* `1 <= sz <= 30`
* `0 <= Node.val <= 100`
* `1 <= n <= sz`
**Follow up:** Could you do this in one pass? | Maintain two pointers and update one with a delay of n steps. |
Please Upvote ( If you find it helpful ) | remove-nth-node-from-end-of-list | 0 | 1 | # Intuition\nSimple intution delay the slow_pointer by n+1 after fast pointer and then iterate till fast_pointer.next does not becomes None. Delete the required node by slow_pointer.next = slow_pointer.next.next \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:\n\n if head.next == None:\n return None\n\n elif n == 1:\n temp1 = head\n\n while temp1.next != None:\n temp2 = temp1\n temp1 = temp1.next\n\n temp2.next = None\n return head\n \n fast_pointer = head\n delayed_pointer = head\n\n while n != 0:\n fast_pointer = fast_pointer.next\n\n n -= 1\n\n if fast_pointer == None:\n head = head.next\n return head\n\n while fast_pointer.next != None:\n fast_pointer = fast_pointer.next\n delayed_pointer = delayed_pointer.next\n\n\n # print(delayed_pointer.val)\n\n\n delayed_pointer.next = delayed_pointer.next.next\n\n return head\n\n \n\n``` | 2 | Given the `head` of a linked list, remove the `nth` node from the end of the list and return its head.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], n = 2
**Output:** \[1,2,3,5\]
**Example 2:**
**Input:** head = \[1\], n = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[1,2\], n = 1
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is `sz`.
* `1 <= sz <= 30`
* `0 <= Node.val <= 100`
* `1 <= n <= sz`
**Follow up:** Could you do this in one pass? | Maintain two pointers and update one with a delay of n steps. |
Python3 | Beats 95% | Efficient Removal of Nth Node from the End of a Linked List | remove-nth-node-from-end-of-list | 0 | 1 | # Solution no. 01\nThe first solution helps you understand the basics with simple steps. \n\n# Intuition\n\nTo determine the node to remove, which is n positions from the end, we need to figure out how many positions we should move from the front to reach the desired node. By counting the total number of nodes in the linked list, we gain this insight and can then adjust the connections accordingly to remove the targeted node from the end.\n\n# Approach\n1. Count the total number of nodes in the linked list by traversing it with a curr pointer.\n1. Calculate the position to move from the front to reach the node n positions from the end.\n1. Reset the count and curr to traverse the list again.\n1. If the node to be removed is the first node, return head.next.\n1. Traverse the list while keeping track of the count.\n1. When the count matches the calculated position before the node to be removed, update the connection to skip the node.\n1. Exit the loop after performing the removal.\n1. Return the updated head.\n\n# Complexity\n- Time complexity:\nWe traverse the linked list twice, so the time complexity is O(n), where n is the number of nodes in the list.\n\n- Space complexity:\nWe only use a few variables, so the space complexity is O(1).\n\n# Code\n```\nclass Solution:\n def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:\n count = 0\n curr = head\n while curr:\n count += 1\n curr = curr.next\n\n check = count - n - 1\n count = 0\n curr = head\n\n # Removing the first node\n if check == -1: \n return head.next\n\n while curr:\n if count == check:\n curr.next = curr.next.next\n # As the removal is done, Exit the loop\n break \n curr = curr.next\n count += 1\n\n return head\n\n```\n\n\n---\n\n# Solution no. 02\n\n# Intuition\nIn our first approach we counted the total number of nodes in the linked list and then identify the n-th node from the end by its position from the beginning. While this counting approach could work, it involves traversing the list twice: once to count the nodes and once to find the node to remove. This double traversal can be inefficient, especially for large lists.\n\nA more efficient approach comes from recognizing that we don\'t really need to know the total number of nodes in the list to solve this problem. Instead, we can utilize two pointers to maintain a specific gap between them as they traverse the list. This gap will be the key to identifying the n-th node from the end.\n\n# Approach\n1. We\'ll use two pointers, first and second, initialized to a dummy node at the beginning of the linked list. The goal is to maintain a gap of n+1 nodes between the two pointers as we traverse the list.\n\n1. Move the first pointer n+1 steps ahead, creating a gap of n nodes between first and second.\n\n1. Now, move both first and second pointers one step at a time until the first pointer reaches the end of the list. This ensures that the gap between the two pointers remains constant at n nodes.\n\n1. When first reaches the end, the second pointer will be pointing to the node right before the node we want to remove (n-th node from the end).\n\n1. Update the second.next pointer to skip the n-th node, effectively removing it from the list.\n\n# Complexity\n- Time complexity:\n The solution involves a single pass through the linked list, so the time complexity is **O(N)**, where N is the number of nodes in the linked list.\n\n- Space complexity:\nWe are using a constant amount of extra space to store the dummy, first, and second pointers, so the space complexity is **O(1)**.\n\n# Code\n```\nclass Solution:\n def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:\n dummy = ListNode(0)\n dummy.next = head\n \n first = dummy\n second = dummy\n \n # Advance first pointer so that the gap between first and second is n+1 nodes apart\n for i in range(n+1):\n first = first.next\n \n # Move first to the end, maintaining the gap\n while first:\n first = first.next\n second = second.next\n \n # Remove the nth node from the end\n second.next = second.next.next\n \n return dummy.next \n\n```\n\n | 9 | Given the `head` of a linked list, remove the `nth` node from the end of the list and return its head.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], n = 2
**Output:** \[1,2,3,5\]
**Example 2:**
**Input:** head = \[1\], n = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[1,2\], n = 1
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is `sz`.
* `1 <= sz <= 30`
* `0 <= Node.val <= 100`
* `1 <= n <= sz`
**Follow up:** Could you do this in one pass? | Maintain two pointers and update one with a delay of n steps. |
19. Two pointer technique using | Python | remove-nth-node-from-end-of-list | 0 | 1 | # Code\n```\nclass Solution:\n def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:\n first, second = head, head\n for x in range(n):\n second = second.next\n while second:\n nex = first.next\n second = second.next\n if second is None:\n first.next = nex.next\n break\n else: first = first.next\n else:\n if n == 1: head = None\n else: head = head.next\n return head\n\n``` | 1 | Given the `head` of a linked list, remove the `nth` node from the end of the list and return its head.
**Example 1:**
**Input:** head = \[1,2,3,4,5\], n = 2
**Output:** \[1,2,3,5\]
**Example 2:**
**Input:** head = \[1\], n = 1
**Output:** \[\]
**Example 3:**
**Input:** head = \[1,2\], n = 1
**Output:** \[1\]
**Constraints:**
* The number of nodes in the list is `sz`.
* `1 <= sz <= 30`
* `0 <= Node.val <= 100`
* `1 <= n <= sz`
**Follow up:** Could you do this in one pass? | Maintain two pointers and update one with a delay of n steps. |
Very Easy || 100% || Fully Explained (C++, Java, Python, JS, Python3) | valid-parentheses | 1 | 1 | An input string is valid if:\n1. Open brackets must be closed by the same type of brackets.\n2. Open brackets must be closed in the correct order.\n\n# **C++ Solution:**\nRuntime: 0 ms, faster than 100.00% of C++ online submissions for Valid Parentheses.\n```\nclass Solution {\npublic:\n bool isValid(string s) {\n // Initialize a stack and a index idx = 0...\n stack<char> stack;\n int idx = 0;\n // If the string is empty, return true...\n if(s.size() == 0){\n return true;\n }\n // Create a loop to check parentheses...\n while(idx < s.size()){\n // If it contains the below parentheses, push the char to stack...\n if( s[idx] == \'(\' || s[idx] == \'[\' || s[idx] == \'{\' ){\n stack.push(s[idx]);\n }\n // If the current char is a closing brace provided, pop the top element...\n // Stack is not empty...\n else if ( (s[idx] == \')\' && !stack.empty() && stack.top() == \'(\') ||\n (s[idx] == \'}\' && !stack.empty() && stack.top() == \'{\') ||\n (s[idx] == \']\' && !stack.empty() && stack.top() == \'[\')\n ){\n stack.pop();\n }\n else {\n return false; // If The string is not a valid parenthesis...\n }\n idx++; // Increase the index...\n }\n // If stack.empty(), return true...\n if(stack.empty()) {\n return true;\n }\n return false;\n }\n};\n```\n\n# **Java Solution (Using Hashmap):**\n```\nclass Solution {\n public boolean isValid(String s) {\n // Create hashmap to store the pairs...\n HashMap<Character, Character> Hmap = new HashMap<Character, Character>();\n Hmap.put(\')\',\'(\');\n Hmap.put(\'}\',\'{\');\n Hmap.put(\']\',\'[\');\n // Create stack data structure...\n Stack<Character> stack = new Stack<Character>();\n // Traverse each charater in input string...\n for (int idx = 0; idx < s.length(); idx++){\n // If open parentheses are present, push it to stack...\n if (s.charAt(idx) == \'(\' || s.charAt(idx) == \'{\' || s.charAt(idx) == \'[\') {\n stack.push(s.charAt(idx));\n continue;\n }\n // If the character is closing parentheses, check that the same type opening parentheses is being pushed to the stack or not...\n // If not, we need to return false...\n if (stack.size() == 0 || Hmap.get(s.charAt(idx)) != stack.pop()) {\n return false;\n }\n }\n // If the stack is empty, return true...\n if (stack.size() == 0) {\n return true;\n }\n return false;\n }\n}\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def isValid(self, s):\n # Create a pair of opening and closing parrenthesis...\n opcl = dict((\'()\', \'[]\', \'{}\'))\n # Create stack data structure...\n stack = []\n # Traverse each charater in input string...\n for idx in s:\n # If open parentheses are present, append it to stack...\n if idx in \'([{\':\n stack.append(idx)\n # If the character is closing parentheses, check that the same type opening parentheses is being pushed to the stack or not...\n # If not, we need to return false...\n elif len(stack) == 0 or idx != opcl[stack.pop()]:\n return False\n # At last, we check if the stack is empty or not...\n # If the stack is empty it means every opened parenthesis is being closed and we can return true, otherwise we return false...\n return len(stack) == 0\n```\n \n# **JavaScript Solution:**\n```\nvar isValid = function(s) {\n // Initialize stack to store the closing brackets expected...\n let stack = [];\n // Traverse each charater in input string...\n for (let idx = 0; idx < s.length; idx++) {\n // If open parentheses are present, push it to stack...\n if (s[idx] == \'{\') {\n stack.push(\'}\');\n } else if (s[idx] == \'[\') {\n stack.push(\']\');\n } else if (s[idx] == \'(\') {\n stack.push(\')\');\n }\n // If a close bracket is found, check that it matches the last stored open bracket\n else if (stack.pop() !== s[idx]) {\n return false;\n }\n }\n return !stack.length;\n};\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n # Create a pair of opening and closing parrenthesis...\n opcl = dict((\'()\', \'[]\', \'{}\'))\n # Create stack data structure...\n stack = []\n # Traverse each charater in input string...\n for idx in s:\n # If open parentheses are present, append it to stack...\n if idx in \'([{\':\n stack.append(idx)\n # If the character is closing parentheses, check that the same type opening parentheses is being pushed to the stack or not...\n # If not, we need to return false...\n elif len(stack) == 0 or idx != opcl[stack.pop()]:\n return False\n # At last, we check if the stack is empty or not...\n # If the stack is empty it means every opened parenthesis is being closed and we can return true, otherwise we return false...\n return len(stack) == 0\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 385 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Very Easy || 100% || Fully Explained (C++, Java, Python, JS, Python3) | valid-parentheses | 1 | 1 | An input string is valid if:\n1. Open brackets must be closed by the same type of brackets.\n2. Open brackets must be closed in the correct order.\n\n# **C++ Solution:**\nRuntime: 0 ms, faster than 100.00% of C++ online submissions for Valid Parentheses.\n```\nclass Solution {\npublic:\n bool isValid(string s) {\n // Initialize a stack and a index idx = 0...\n stack<char> stack;\n int idx = 0;\n // If the string is empty, return true...\n if(s.size() == 0){\n return true;\n }\n // Create a loop to check parentheses...\n while(idx < s.size()){\n // If it contains the below parentheses, push the char to stack...\n if( s[idx] == \'(\' || s[idx] == \'[\' || s[idx] == \'{\' ){\n stack.push(s[idx]);\n }\n // If the current char is a closing brace provided, pop the top element...\n // Stack is not empty...\n else if ( (s[idx] == \')\' && !stack.empty() && stack.top() == \'(\') ||\n (s[idx] == \'}\' && !stack.empty() && stack.top() == \'{\') ||\n (s[idx] == \']\' && !stack.empty() && stack.top() == \'[\')\n ){\n stack.pop();\n }\n else {\n return false; // If The string is not a valid parenthesis...\n }\n idx++; // Increase the index...\n }\n // If stack.empty(), return true...\n if(stack.empty()) {\n return true;\n }\n return false;\n }\n};\n```\n\n# **Java Solution (Using Hashmap):**\n```\nclass Solution {\n public boolean isValid(String s) {\n // Create hashmap to store the pairs...\n HashMap<Character, Character> Hmap = new HashMap<Character, Character>();\n Hmap.put(\')\',\'(\');\n Hmap.put(\'}\',\'{\');\n Hmap.put(\']\',\'[\');\n // Create stack data structure...\n Stack<Character> stack = new Stack<Character>();\n // Traverse each charater in input string...\n for (int idx = 0; idx < s.length(); idx++){\n // If open parentheses are present, push it to stack...\n if (s.charAt(idx) == \'(\' || s.charAt(idx) == \'{\' || s.charAt(idx) == \'[\') {\n stack.push(s.charAt(idx));\n continue;\n }\n // If the character is closing parentheses, check that the same type opening parentheses is being pushed to the stack or not...\n // If not, we need to return false...\n if (stack.size() == 0 || Hmap.get(s.charAt(idx)) != stack.pop()) {\n return false;\n }\n }\n // If the stack is empty, return true...\n if (stack.size() == 0) {\n return true;\n }\n return false;\n }\n}\n```\n\n# **Python Solution:**\n```\nclass Solution(object):\n def isValid(self, s):\n # Create a pair of opening and closing parrenthesis...\n opcl = dict((\'()\', \'[]\', \'{}\'))\n # Create stack data structure...\n stack = []\n # Traverse each charater in input string...\n for idx in s:\n # If open parentheses are present, append it to stack...\n if idx in \'([{\':\n stack.append(idx)\n # If the character is closing parentheses, check that the same type opening parentheses is being pushed to the stack or not...\n # If not, we need to return false...\n elif len(stack) == 0 or idx != opcl[stack.pop()]:\n return False\n # At last, we check if the stack is empty or not...\n # If the stack is empty it means every opened parenthesis is being closed and we can return true, otherwise we return false...\n return len(stack) == 0\n```\n \n# **JavaScript Solution:**\n```\nvar isValid = function(s) {\n // Initialize stack to store the closing brackets expected...\n let stack = [];\n // Traverse each charater in input string...\n for (let idx = 0; idx < s.length; idx++) {\n // If open parentheses are present, push it to stack...\n if (s[idx] == \'{\') {\n stack.push(\'}\');\n } else if (s[idx] == \'[\') {\n stack.push(\']\');\n } else if (s[idx] == \'(\') {\n stack.push(\')\');\n }\n // If a close bracket is found, check that it matches the last stored open bracket\n else if (stack.pop() !== s[idx]) {\n return false;\n }\n }\n return !stack.length;\n};\n```\n\n# **Python3 Solution:**\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n # Create a pair of opening and closing parrenthesis...\n opcl = dict((\'()\', \'[]\', \'{}\'))\n # Create stack data structure...\n stack = []\n # Traverse each charater in input string...\n for idx in s:\n # If open parentheses are present, append it to stack...\n if idx in \'([{\':\n stack.append(idx)\n # If the character is closing parentheses, check that the same type opening parentheses is being pushed to the stack or not...\n # If not, we need to return false...\n elif len(stack) == 0 or idx != opcl[stack.pop()]:\n return False\n # At last, we check if the stack is empty or not...\n # If the stack is empty it means every opened parenthesis is being closed and we can return true, otherwise we return false...\n return len(stack) == 0\n```\n**I am working hard for you guys...\nPlease upvote if you find any help with this code...** | 385 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
[VIDEO] Step-by-Step Visualization Using a Stack | valid-parentheses | 0 | 1 | https://youtube.com/watch?v=YwvHeouhy6s\n\nSince the **last** bracket that is opened must also be the **first** one to be closed, it makes sense to use a data structure that uses the **Last In, First Out** (LIFO) principle. Therefore, a **stack** is a good choice here.\n\nIf a bracket is an *opening* bracet, we\'ll just push it on to the stack. If it\'s a *closing* bracket, then we\'ll use the `pairs` dictionary to check if it\'s the correct type of bracket (first pop the last opening bracket encountered, find the corresponding closing bracket, and compare it with the current bracket in the loop). If the wrong type of closing bracket is found, then we can exit early and return False.\n\nIf we make it all the way to the end and all open brackets have been closed, then the stack should be empty. This is why we `return len(stack) == 0` at the end. This will return `True` if the stack is empty, and `False` if it\'s not.\n\n```\nclass Solution(object):\n def isValid(self, s):\n stack = [] # only use append and pop\n pairs = {\n \'(\': \')\',\n \'{\': \'}\',\n \'[\': \']\'\n }\n for bracket in s:\n if bracket in pairs:\n stack.append(bracket)\n elif len(stack) == 0 or bracket != pairs[stack.pop()]:\n return False\n\n return len(stack) == 0\n\n``` | 28 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
[VIDEO] Step-by-Step Visualization Using a Stack | valid-parentheses | 0 | 1 | https://youtube.com/watch?v=YwvHeouhy6s\n\nSince the **last** bracket that is opened must also be the **first** one to be closed, it makes sense to use a data structure that uses the **Last In, First Out** (LIFO) principle. Therefore, a **stack** is a good choice here.\n\nIf a bracket is an *opening* bracet, we\'ll just push it on to the stack. If it\'s a *closing* bracket, then we\'ll use the `pairs` dictionary to check if it\'s the correct type of bracket (first pop the last opening bracket encountered, find the corresponding closing bracket, and compare it with the current bracket in the loop). If the wrong type of closing bracket is found, then we can exit early and return False.\n\nIf we make it all the way to the end and all open brackets have been closed, then the stack should be empty. This is why we `return len(stack) == 0` at the end. This will return `True` if the stack is empty, and `False` if it\'s not.\n\n```\nclass Solution(object):\n def isValid(self, s):\n stack = [] # only use append and pop\n pairs = {\n \'(\': \')\',\n \'{\': \'}\',\n \'[\': \']\'\n }\n for bracket in s:\n if bracket in pairs:\n stack.append(bracket)\n elif len(stack) == 0 or bracket != pairs[stack.pop()]:\n return False\n\n return len(stack) == 0\n\n``` | 28 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Is this a Valid Parentheses??? | valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code checks whether a given string containing only parentheses, brackets, and curly braces is valid in terms of their arrangement. A valid string should have each opening bracket matched with its corresponding closing bracket in the correct order.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code uses a stack to keep track of the opening brackets encountered so far. When a closing bracket is encountered, it is checked if it matches the last opening bracket. If it does, the last opening bracket is popped from the stack. If there is a mismatch or if the stack is empty when a closing bracket is encountered, the string is considered invalid.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(n), where n is the length of the input string. In the worst case, the algorithm iterates through each character in the string once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n), where n is the length of the input string. In the worst case, the stack can grow to the size of the input string when all characters are opening brackets.\n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n # Dictionary to store the mapping of opening and closing brackets\n brackets = {\'(\':\')\', \'{\':\'}\', \'[\':\']\'}\n \n # Stack to keep track of opening brackets\n stack = []\n \n # Iterate through each character in the input string\n for i in s:\n # If the character is an opening bracket, push it onto the stack\n if i in brackets:\n stack.append(i)\n else:\n # If the stack is empty or the current closing bracket doesn\'t match\n # the corresponding opening bracket, return False\n if len(stack) == 0 or i != brackets[stack.pop()]:\n return False\n \n # Check if there are any remaining opening brackets in the stack\n return len(stack) == 0\n\n``` | 7 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Is this a Valid Parentheses??? | valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code checks whether a given string containing only parentheses, brackets, and curly braces is valid in terms of their arrangement. A valid string should have each opening bracket matched with its corresponding closing bracket in the correct order.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code uses a stack to keep track of the opening brackets encountered so far. When a closing bracket is encountered, it is checked if it matches the last opening bracket. If it does, the last opening bracket is popped from the stack. If there is a mismatch or if the stack is empty when a closing bracket is encountered, the string is considered invalid.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(n), where n is the length of the input string. In the worst case, the algorithm iterates through each character in the string once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n), where n is the length of the input string. In the worst case, the stack can grow to the size of the input string when all characters are opening brackets.\n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n # Dictionary to store the mapping of opening and closing brackets\n brackets = {\'(\':\')\', \'{\':\'}\', \'[\':\']\'}\n \n # Stack to keep track of opening brackets\n stack = []\n \n # Iterate through each character in the input string\n for i in s:\n # If the character is an opening bracket, push it onto the stack\n if i in brackets:\n stack.append(i)\n else:\n # If the stack is empty or the current closing bracket doesn\'t match\n # the corresponding opening bracket, return False\n if len(stack) == 0 or i != brackets[stack.pop()]:\n return False\n \n # Check if there are any remaining opening brackets in the stack\n return len(stack) == 0\n\n``` | 7 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
PythonEasy | valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n while \'()\' in s or \'[]\'in s or \'{}\' in s:\n s = s.replace(\'()\',\'\').replace(\'[]\',\'\').replace(\'{}\',\'\')\n return False if len(s) !=0 else True\n``` | 114 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
PythonEasy | valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n while \'()\' in s or \'[]\'in s or \'{}\' in s:\n s = s.replace(\'()\',\'\').replace(\'[]\',\'\').replace(\'{}\',\'\')\n return False if len(s) !=0 else True\n``` | 114 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Python code for determining if the string has valid parentheses (TC&SC: O(n)) | valid-parentheses | 0 | 1 | # Intuition\nThe code utilizes a stack data structure to keep track of open brackets (e.g., \'(\', \'[\', \'{\'). It iterates through the input string, and for each bracket character, it performs the following checks:\n\nIf it\'s an open bracket, it pushes it onto the stack.\nIf it\'s a closing bracket, it checks if the corresponding open bracket is at the top of the stack. If it is, the open bracket is popped from the stack.\nIf there\'s any mismatch or the stack is not empty at the end, the string is considered invalid. Otherwise, it\'s valid.\n\n# Approach\nInitialize an empty stack to hold open brackets.\nCheck for some quick invalidity checks:\nIf the length of the string is 1, return False. Single brackets cannot form a valid sequence.\nIf the first character in the string is a closing bracket (\')\', \']\', \'}\'), return False. A valid sequence should start with an open bracket.\nLoop through the characters of the input string s:\nIf the character is an open bracket (\'(\', \'[\', \'{\'), push it onto the stack.\nIf the character is a closing bracket (\')\', \']\', \'}\'), check if the stack is empty. If it\'s empty, return False because there\'s no corresponding open bracket for the current closing bracket.\nIf the stack is not empty, check if the top of the stack matches the expected open bracket for the current closing bracket. If it matches, pop the open bracket from the stack.\nIf there\'s no match, return False because the brackets are not properly nested.\nAfter processing all characters in the string, check if the stack is empty. If it\'s empty, return True because all open brackets have been properly closed.\nIf the stack is not empty at this point, it means there are open brackets without matching closing brackets, so return False.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n stack = []\n if len(s) == 1:\n return False\n elif s[0] == ")" or s[0] == "]" or s[0] == "}":\n return False\n else:\n for i in range(len(s)):\n if s[i] == "(" or s[i] == "[" or s[i] == "{":\n stack.append(s[i])\n elif s[i] == ")" and "(" in stack:\n if stack[-1] == "(":\n stack.pop()\n elif s[i] == "]" and "[" in stack:\n if stack[-1] == "[":\n stack.pop()\n elif s[i] == "}" and "{" in stack:\n if stack[-1] == "{":\n stack.pop()\n else:\n return False\n if stack == []:\n return True\n``` | 2 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Python code for determining if the string has valid parentheses (TC&SC: O(n)) | valid-parentheses | 0 | 1 | # Intuition\nThe code utilizes a stack data structure to keep track of open brackets (e.g., \'(\', \'[\', \'{\'). It iterates through the input string, and for each bracket character, it performs the following checks:\n\nIf it\'s an open bracket, it pushes it onto the stack.\nIf it\'s a closing bracket, it checks if the corresponding open bracket is at the top of the stack. If it is, the open bracket is popped from the stack.\nIf there\'s any mismatch or the stack is not empty at the end, the string is considered invalid. Otherwise, it\'s valid.\n\n# Approach\nInitialize an empty stack to hold open brackets.\nCheck for some quick invalidity checks:\nIf the length of the string is 1, return False. Single brackets cannot form a valid sequence.\nIf the first character in the string is a closing bracket (\')\', \']\', \'}\'), return False. A valid sequence should start with an open bracket.\nLoop through the characters of the input string s:\nIf the character is an open bracket (\'(\', \'[\', \'{\'), push it onto the stack.\nIf the character is a closing bracket (\')\', \']\', \'}\'), check if the stack is empty. If it\'s empty, return False because there\'s no corresponding open bracket for the current closing bracket.\nIf the stack is not empty, check if the top of the stack matches the expected open bracket for the current closing bracket. If it matches, pop the open bracket from the stack.\nIf there\'s no match, return False because the brackets are not properly nested.\nAfter processing all characters in the string, check if the stack is empty. If it\'s empty, return True because all open brackets have been properly closed.\nIf the stack is not empty at this point, it means there are open brackets without matching closing brackets, so return False.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n stack = []\n if len(s) == 1:\n return False\n elif s[0] == ")" or s[0] == "]" or s[0] == "}":\n return False\n else:\n for i in range(len(s)):\n if s[i] == "(" or s[i] == "[" or s[i] == "{":\n stack.append(s[i])\n elif s[i] == ")" and "(" in stack:\n if stack[-1] == "(":\n stack.pop()\n elif s[i] == "]" and "[" in stack:\n if stack[-1] == "[":\n stack.pop()\n elif s[i] == "}" and "{" in stack:\n if stack[-1] == "{":\n stack.pop()\n else:\n return False\n if stack == []:\n return True\n``` | 2 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
👹Simple Stack Checker, readable, python, java 🐍☕ | valid-parentheses | 1 | 1 | # Intuition\nthink of it with simple logic, if (, then i+1 aka next element needs to be ), if not return false\n\n# Approach\ncreate stack\ncreate mapping of \'(\'to\')\' and so on\norder of if this is keys or this is values doesn\'t matter\nitterate through string, if i in values (in my code), push to stack aka append, then next value needs to be in the keys, and needs to be mapped to my i directly, if not false, boom.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# PYTHON\n```\n\nclass Solution:\n def isValid(self, s: str) -> bool:\n\n #create empty stack\n stack = []\n #keys left, values right\n mapping = {\')\':\'(\',\'}\':\'{\',\']\':\'[\'}\n\n for char in s:\n if char in mapping.values():\n stack.append(char)\n elif char in mapping.keys():\n if not stack or stack.pop() != mapping[char]: #if they don\'t match you leave with false\n return False\n return len(stack)==0\n```\n# JAVA\n```\nimport java.util.Stack;\n\npublic class Solution {\n public boolean isValid(String s) {\n Stack<Character> stack = new Stack<>();\n char[] chars = s.toCharArray();\n // Keys are on the right side, values are on the left side\n char[] keys = {\')\', \'}\', \']\'};\n char[] values = {\'(\', \'{\', \'[\'};\n\n for (char c : chars) {\n if (contains(values, c)) {\n stack.push(c);\n } else if (contains(keys, c)) {\n if (stack.isEmpty() || stack.pop() != getMatchingValue(c)) {\n return false;\n }\n }\n }\n \n return stack.isEmpty();\n }\n\n private boolean contains(char[] arr, char target) {\n for (char c : arr) {\n if (c == target) {\n return true;\n }\n }\n return false;\n }\n \n private char getMatchingValue(char key) {\n switch (key) {\n case \')\':\n return \'(\';\n case \'}\':\n return \'{\';\n case \']\':\n return \'[\';\n default:\n return \'\\0\'; // Invalid character\n }\n }\n}\n\n```\n\n\n | 2 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
👹Simple Stack Checker, readable, python, java 🐍☕ | valid-parentheses | 1 | 1 | # Intuition\nthink of it with simple logic, if (, then i+1 aka next element needs to be ), if not return false\n\n# Approach\ncreate stack\ncreate mapping of \'(\'to\')\' and so on\norder of if this is keys or this is values doesn\'t matter\nitterate through string, if i in values (in my code), push to stack aka append, then next value needs to be in the keys, and needs to be mapped to my i directly, if not false, boom.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# PYTHON\n```\n\nclass Solution:\n def isValid(self, s: str) -> bool:\n\n #create empty stack\n stack = []\n #keys left, values right\n mapping = {\')\':\'(\',\'}\':\'{\',\']\':\'[\'}\n\n for char in s:\n if char in mapping.values():\n stack.append(char)\n elif char in mapping.keys():\n if not stack or stack.pop() != mapping[char]: #if they don\'t match you leave with false\n return False\n return len(stack)==0\n```\n# JAVA\n```\nimport java.util.Stack;\n\npublic class Solution {\n public boolean isValid(String s) {\n Stack<Character> stack = new Stack<>();\n char[] chars = s.toCharArray();\n // Keys are on the right side, values are on the left side\n char[] keys = {\')\', \'}\', \']\'};\n char[] values = {\'(\', \'{\', \'[\'};\n\n for (char c : chars) {\n if (contains(values, c)) {\n stack.push(c);\n } else if (contains(keys, c)) {\n if (stack.isEmpty() || stack.pop() != getMatchingValue(c)) {\n return false;\n }\n }\n }\n \n return stack.isEmpty();\n }\n\n private boolean contains(char[] arr, char target) {\n for (char c : arr) {\n if (c == target) {\n return true;\n }\n }\n return false;\n }\n \n private char getMatchingValue(char key) {\n switch (key) {\n case \')\':\n return \'(\';\n case \'}\':\n return \'{\';\n case \']\':\n return \'[\';\n default:\n return \'\\0\'; // Invalid character\n }\n }\n}\n\n```\n\n\n | 2 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Python 4ms Faster then 100% with explanation | valid-parentheses | 0 | 1 | ```\nclass Solution(object):\n\tdef isValid(self, s):\n """\n :type s: str\n :rtype: bool\n """\n d = {\'(\':\')\', \'{\':\'}\',\'[\':\']\'}\n stack = []\n for i in s:\n if i in d: # 1\n stack.append(i)\n elif len(stack) == 0 or d[stack.pop()] != i: # 2\n return False\n return len(stack) == 0 # 3\n\t\n# 1. if it\'s the left bracket then we append it to the stack\n# 2. else if it\'s the right bracket and the stack is empty(meaning no matching left bracket), or the left bracket doesn\'t match\n# 3. finally check if the stack still contains unmatched left bracket\n``` | 434 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Python 4ms Faster then 100% with explanation | valid-parentheses | 0 | 1 | ```\nclass Solution(object):\n\tdef isValid(self, s):\n """\n :type s: str\n :rtype: bool\n """\n d = {\'(\':\')\', \'{\':\'}\',\'[\':\']\'}\n stack = []\n for i in s:\n if i in d: # 1\n stack.append(i)\n elif len(stack) == 0 or d[stack.pop()] != i: # 2\n return False\n return len(stack) == 0 # 3\n\t\n# 1. if it\'s the left bracket then we append it to the stack\n# 2. else if it\'s the right bracket and the stack is empty(meaning no matching left bracket), or the left bracket doesn\'t match\n# 3. finally check if the stack still contains unmatched left bracket\n``` | 434 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
solutuion for u :) | valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n dick = {"(":")", \'[\':\']\', \'{\':\'}\'}\n\n inp = []\n \n for i in s:\n \n \n if(i == \'[\' or i == \'{\' or i == \'(\'):\n inp.append(i)\n \n elif(i == \']\' or i==\'}\' or i == \')\'):\n if len(inp)==0:\n return False\n x = inp.pop()\n if dick[x] == i:\n continue\n else:\n return False\n if(len(inp) != 0):\n return False \n else:\n return True \n \n \n``` | 1 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
solutuion for u :) | valid-parentheses | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n dick = {"(":")", \'[\':\']\', \'{\':\'}\'}\n\n inp = []\n \n for i in s:\n \n \n if(i == \'[\' or i == \'{\' or i == \'(\'):\n inp.append(i)\n \n elif(i == \']\' or i==\'}\' or i == \')\'):\n if len(inp)==0:\n return False\n x = inp.pop()\n if dick[x] == i:\n continue\n else:\n return False\n if(len(inp) != 0):\n return False \n else:\n return True \n \n \n``` | 1 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
✅Beats 100%|💡O(n) solution with 100% Acceptance Rate with Easy and Detailed Explanation 💡😄 | valid-parentheses | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use a stack to maintain the order of open brackets encountered.\nWhen a closing bracket is encountered, we check if it matches the last encountered open bracket.\nIf the brackets are balanced and correctly ordered, the stack should be empty at the end.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach used here is to iterate through the input string s character by character. We maintain a stack to keep track of open brackets encountered. When we encounter an open bracket (\'(\', \'{\', or \'[\'), we push it onto the stack. When we encounter a closing bracket (\')\', \'}\', or \']\'), we check if there is a matching open bracket at the top of the stack. If not, it means the brackets are not balanced, and we return false. If there is a matching open bracket, we pop it from the stack.\n\nAt the end of the loop, if the stack is empty, it indicates that all open brackets have been closed properly, and we return true. Otherwise, if there are unmatched open brackets left in the stack, we return false.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(n), where n is the length of the input string s. This is because we iterate through the string once, and each character operation takes constant time.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) as well, where n is the length of the input string s. In the worst case, all characters in the string could be open brackets, and they would be pushed onto the stack.\n\n---\n\n\n# \uD83D\uDCA1"If you have come this far, I would like to kindly request your support by upvoting this solution, thus enabling it to reach a broader audience."\u2763\uFE0F\uD83D\uDCA1\n\n---\n\n\n# Code\n\n```C++ []\n#include <stack>\n#include <string>\n\nclass Solution {\npublic:\n bool isValid(string s) {\n stack<char> brackets;\n \n for (char c : s) {\n if (c == \'(\' || c == \'{\' || c == \'[\') {\n brackets.push(c);\n } else {\n if (brackets.empty()) {\n return false; // There\'s no matching open bracket.\n }\n \n char openBracket = brackets.top();\n brackets.pop();\n \n if ((c == \')\' && openBracket != \'(\') ||\n (c == \'}\' && openBracket != \'{\') ||\n (c == \']\' && openBracket != \'[\')) {\n return false; // Mismatched closing bracket.\n }\n }\n }\n \n return brackets.empty(); // All open brackets should be closed.\n }\n};\n```\n```Java []\nimport java.util.Stack;\n\nclass Solution {\n public boolean isValid(String s) {\n Stack<Character> brackets = new Stack<>();\n \n for (char c : s.toCharArray()) {\n if (c == \'(\' || c == \'{\' || c == \'[\') {\n brackets.push(c);\n } else {\n if (brackets.isEmpty()) {\n return false; // There\'s no matching open bracket.\n }\n \n char openBracket = brackets.pop();\n \n if ((c == \')\' && openBracket != \'(\') ||\n (c == \'}\' && openBracket != \'{\') ||\n (c == \']\' && openBracket != \'[\')) {\n return false; // Mismatched closing bracket.\n }\n }\n }\n \n return brackets.isEmpty(); // All open brackets should be closed.\n }\n}\n\n```\n```Python []\nclass Solution:\n def isValid(self, s: str) -> bool:\n brackets = []\n \n for c in s:\n if c in \'({[\':\n brackets.append(c)\n else:\n if not brackets:\n return False # There\'s no matching open bracket.\n \n open_bracket = brackets.pop()\n \n if (c == \')\' and open_bracket != \'(\') or (c == \'}\' and open_bracket != \'{\') or (c == \']\' and open_bracket != \'[\'):\n return False # Mismatched closing bracket.\n \n return not brackets # All open brackets should be closed.\n\n```\n```Javascript []\nvar isValid = function(s) {\n const brackets = [];\n \n for (let c of s) {\n if (c === \'(\' || c === \'{\' || c === \'[\') {\n brackets.push(c);\n } else {\n if (brackets.length === 0) {\n return false; // There\'s no matching open bracket.\n }\n \n const openBracket = brackets.pop();\n \n if ((c === \')\' && openBracket !== \'(\') || (c === \'}\' && openBracket !== \'{\') || (c === \']\' && openBracket !== \'[\')) {\n return false; // Mismatched closing bracket.\n }\n }\n }\n \n return brackets.length === 0; // All open brackets should be closed.\n};\n\n```\n```Ruby []\ndef is_valid(s)\n brackets = []\n \n s.chars.each do |c|\n if c == \'(\' || c == \'{\' || c == \'[\'\n brackets.push(c)\n else\n if brackets.empty?\n return false # There\'s no matching open bracket.\n end\n \n open_bracket = brackets.pop\n \n if (c == \')\' && open_bracket != \'(\') || (c == \'}\' && open_bracket != \'{\') || (c == \']\' && open_bracket != \'[\')\n return false # Mismatched closing bracket.\n end\n end\n end\n \n brackets.empty? # All open brackets should be closed.\nend\n\n``` | 7 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
✅Beats 100%|💡O(n) solution with 100% Acceptance Rate with Easy and Detailed Explanation 💡😄 | valid-parentheses | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use a stack to maintain the order of open brackets encountered.\nWhen a closing bracket is encountered, we check if it matches the last encountered open bracket.\nIf the brackets are balanced and correctly ordered, the stack should be empty at the end.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach used here is to iterate through the input string s character by character. We maintain a stack to keep track of open brackets encountered. When we encounter an open bracket (\'(\', \'{\', or \'[\'), we push it onto the stack. When we encounter a closing bracket (\')\', \'}\', or \']\'), we check if there is a matching open bracket at the top of the stack. If not, it means the brackets are not balanced, and we return false. If there is a matching open bracket, we pop it from the stack.\n\nAt the end of the loop, if the stack is empty, it indicates that all open brackets have been closed properly, and we return true. Otherwise, if there are unmatched open brackets left in the stack, we return false.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(n), where n is the length of the input string s. This is because we iterate through the string once, and each character operation takes constant time.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) as well, where n is the length of the input string s. In the worst case, all characters in the string could be open brackets, and they would be pushed onto the stack.\n\n---\n\n\n# \uD83D\uDCA1"If you have come this far, I would like to kindly request your support by upvoting this solution, thus enabling it to reach a broader audience."\u2763\uFE0F\uD83D\uDCA1\n\n---\n\n\n# Code\n\n```C++ []\n#include <stack>\n#include <string>\n\nclass Solution {\npublic:\n bool isValid(string s) {\n stack<char> brackets;\n \n for (char c : s) {\n if (c == \'(\' || c == \'{\' || c == \'[\') {\n brackets.push(c);\n } else {\n if (brackets.empty()) {\n return false; // There\'s no matching open bracket.\n }\n \n char openBracket = brackets.top();\n brackets.pop();\n \n if ((c == \')\' && openBracket != \'(\') ||\n (c == \'}\' && openBracket != \'{\') ||\n (c == \']\' && openBracket != \'[\')) {\n return false; // Mismatched closing bracket.\n }\n }\n }\n \n return brackets.empty(); // All open brackets should be closed.\n }\n};\n```\n```Java []\nimport java.util.Stack;\n\nclass Solution {\n public boolean isValid(String s) {\n Stack<Character> brackets = new Stack<>();\n \n for (char c : s.toCharArray()) {\n if (c == \'(\' || c == \'{\' || c == \'[\') {\n brackets.push(c);\n } else {\n if (brackets.isEmpty()) {\n return false; // There\'s no matching open bracket.\n }\n \n char openBracket = brackets.pop();\n \n if ((c == \')\' && openBracket != \'(\') ||\n (c == \'}\' && openBracket != \'{\') ||\n (c == \']\' && openBracket != \'[\')) {\n return false; // Mismatched closing bracket.\n }\n }\n }\n \n return brackets.isEmpty(); // All open brackets should be closed.\n }\n}\n\n```\n```Python []\nclass Solution:\n def isValid(self, s: str) -> bool:\n brackets = []\n \n for c in s:\n if c in \'({[\':\n brackets.append(c)\n else:\n if not brackets:\n return False # There\'s no matching open bracket.\n \n open_bracket = brackets.pop()\n \n if (c == \')\' and open_bracket != \'(\') or (c == \'}\' and open_bracket != \'{\') or (c == \']\' and open_bracket != \'[\'):\n return False # Mismatched closing bracket.\n \n return not brackets # All open brackets should be closed.\n\n```\n```Javascript []\nvar isValid = function(s) {\n const brackets = [];\n \n for (let c of s) {\n if (c === \'(\' || c === \'{\' || c === \'[\') {\n brackets.push(c);\n } else {\n if (brackets.length === 0) {\n return false; // There\'s no matching open bracket.\n }\n \n const openBracket = brackets.pop();\n \n if ((c === \')\' && openBracket !== \'(\') || (c === \'}\' && openBracket !== \'{\') || (c === \']\' && openBracket !== \'[\')) {\n return false; // Mismatched closing bracket.\n }\n }\n }\n \n return brackets.length === 0; // All open brackets should be closed.\n};\n\n```\n```Ruby []\ndef is_valid(s)\n brackets = []\n \n s.chars.each do |c|\n if c == \'(\' || c == \'{\' || c == \'[\'\n brackets.push(c)\n else\n if brackets.empty?\n return false # There\'s no matching open bracket.\n end\n \n open_bracket = brackets.pop\n \n if (c == \')\' && open_bracket != \'(\') || (c == \'}\' && open_bracket != \'{\') || (c == \']\' && open_bracket != \'[\')\n return false # Mismatched closing bracket.\n end\n end\n end\n \n brackets.empty? # All open brackets should be closed.\nend\n\n``` | 7 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Simple way for python | valid-parentheses | 0 | 1 | \n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n ack = []\n lookfor = {\')\':\'(\', \'}\':\'{\', \']\':\'[\'}\n\n for p in s:\n if p in lookfor.values():\n ack.append(p)\n elif ack and lookfor[p] == ack[-1]:\n ack.pop()\n else:\n return False\n\n return ack == []\n``` | 12 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
Simple way for python | valid-parentheses | 0 | 1 | \n# Code\n```\nclass Solution:\n def isValid(self, s: str) -> bool:\n ack = []\n lookfor = {\')\':\'(\', \'}\':\'{\', \']\':\'[\'}\n\n for p in s:\n if p in lookfor.values():\n ack.append(p)\n elif ack and lookfor[p] == ack[-1]:\n ack.pop()\n else:\n return False\n\n return ack == []\n``` | 12 | Given a string `s` containing just the characters `'('`, `')'`, `'{'`, `'}'`, `'['` and `']'`, determine if the input string is valid.
An input string is valid if:
1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.
**Example 1:**
**Input:** s = "() "
**Output:** true
**Example 2:**
**Input:** s = "()\[\]{} "
**Output:** true
**Example 3:**
**Input:** s = "(\] "
**Output:** false
**Constraints:**
* `1 <= s.length <= 104`
* `s` consists of parentheses only `'()[]{}'`. | An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
{ { } [ ] [ [ [ ] ] ] } is VALID expression
[ [ [ ] ] ] is VALID sub-expression
{ } [ ] is VALID sub-expression
Can we exploit this recursive structure somehow? What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
{ { ( { } ) } }
|_|
{ { ( ) } }
|______|
{ { } }
|__________|
{ }
|________________|
VALID EXPRESSION! The stack data structure can come in handy here in representing this recursive structure of the problem. We can't really process this from the inside out because we don't have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards. |
✔️ [Python3] MERGING, Explained | merge-two-sorted-lists | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nFor simplicity, we create a dummy node to which we attach nodes from lists. We iterate over lists using two-pointers and build up a resulting list so that values are monotonically increased.\n\nTime: **O(n)**\nSpace: **O(1)**\n\n```\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n cur = dummy = ListNode()\n while list1 and list2: \n if list1.val < list2.val:\n cur.next = list1\n list1, cur = list1.next, list1\n else:\n cur.next = list2\n list2, cur = list2.next, list2\n \n if list1 or list2:\n cur.next = list1 if list1 else list2\n \n return dummy.next\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 1,078 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
(VIDEO) Step-by-Step Visualization and Explanation | merge-two-sorted-lists | 0 | 1 | https://www.youtube.com/watch?v=E5XXiY6QnAs\n\nWe\'ll create a starting node called `head` and use a pointer called `current` to traverse the two lists. At each iteration of the loop, we compare the values of the nodes at list1 and list2, and point `current.next` to the <i>smaller</i> node. Then we advance the pointers and repeat until one of the list pointers reaches the end of the list.\n\nAt this point, there\'s no need to iterate through the rest of the other list because we know that it\'s still in sorted order. So `current.next = list1 or list2` points current.next to the list that still has nodes left. The last step is just to return `head.next`, since head was just a placeholder node and the actual list starts at `head.next`.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution(object):\n def mergeTwoLists(self, list1, list2):\n head = ListNode()\n current = head\n while list1 and list2:\n if list1.val < list2.val:\n current.next = list1\n list1 = list1.next\n else:\n current.next = list2\n list2 = list2.next\n current = current.next\n\n current.next = list1 or list2\n return head.next\n``` | 125 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Binbin's knight needs some rest | merge-two-sorted-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n cur = head = ListNode()\n while list1 and list2:\n if list1.val < list2.val:\n cur.next = list1\n cur = list1\n list1 = list1.next \n else:\n cur.next = list2\n cur = list2\n list2 = list2.next\n if list1 or list2:\n if list1:\n cur.next = list1\n else:\n cur.next = list2\n return head.next\n \n \n``` | 1 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Python3 Solution with a Detailed Explanation - dummy explained | merge-two-sorted-lists | 0 | 1 | [Linkedlists](https://realpython.com/linked-lists-python/) can be confusing especially if you\'ve recently started to code but (I think) once you understand it fully, it should not be that difficult. \n\nFor this problem, I\'m going to explain several ways of solving it **BUT** I want to make something clear. Something that you\'ve seen a lot of times in the posts on this website but probably haven\'t fully understood. `dummy` variable! It has been used significantly in the solutions of this problem and not well explained for a newbie level coder! The idea is we\'re dealing with `pointers` that point to a memory location! Think of it this way! You want to find gold that is hidden somewhere. Someone has put a set of clues in a sequence! Meaning, if you find the first clue and solve the problem hidden in the clue, you will get to the second clue! Solving the hidden problem of second clue will get you to the thrid clue, and so on! If you keep solving, you\'ll get to the gold! `dummy` helps you to find the first clue!!!! \n\nThroughout the solution below, you\'ll be asking yourself why `dummy` is not changing and we eventually return `dummy.next`???? It doesn\'t make sense, right? However, if you think that `dummy` is pointing to the start and there is another variable (`temp`) that makes the linkes from node to node, you\'ll have a better filling! \nSimilar to the gold example if I tell you the first clue is at location X, then, you can solve clues sequentially (because of course you\'re smart) and bingo! you find the gold! Watch [this](https://www.youtube.com/watch?v=3O_f_sk3mFc). \n\nThis video shows why we need the `dummy`! Since we\'re traversing using `temp` but once `temp` gets to the tail of the sorted merged linkedlist, there\'s no way back to the start of the list to return as a result! So `dummy` to the rescue! it does not get changed throughout the list traversals `temp` is doing! So, `dummy` makes sure we don\'t loose the head of the thread (result list). Does this make sense? Alright! Enough with `dummy`! \n\nI think if you get this, the first solution feels natural! Now, watch [this](https://www.youtube.com/watch?v=GfRQvf7MB3k). You got the idea?? Nice! \n\n\nFirst you initialize `dummy` and `temp`. One is sitting at the start of the linkedlist and the other (`temp`) is going to move forward find which value should be added to the list. Note that it\'s initialized with a value `0` but it can be anything! You initialize it with your value of choice! Doesn\'t matter since we\'re going to finally return `dummy.next` which disregards `0` that we used to start the linkedlist. Line `#1` makes sure none of the `l1` and `l2` are empty! If one of them is empty, we should return the other! If both are nonempty, we check `val` of each of them to add the smaller one to the result linkedlist! In line `#2`, `l1.val` is smaller and we want to add it to the list. How? We use `temp` POINTER (it\'s pointer, remember that!). Since we initialized `temp` to have value `0` at first node, we use `temp.next` to point `0` to the next value we\'re going to add to the list `l1.val` (line `#3`). Once we do that, we update `l1` to go to the next node of `l1`. If the `if` statement of line `#2` doesn\'t work, we do similar stuff with `l2`. And finally, if the length of `l1` and `l2` are not the same, we\'re going to the end of one of them at some point! Line `#5` adds whatever left from whatever linkedlist to the `temp.next` (check the above video for a great explanation of this part). Note that both linkedlists were sorted initially. Also, this line takes care of when one of the linkedlists are empty. Finally, we return `dummy.next` since `dummy` is pointing to `0` and `next` to zero is what we\'ve added throughout the process. \n\n```\nclass Solution:\n def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode: \n dummy = temp = ListNode(0)\n while l1 != None and l2 != None: #1\n\n if l1.val < l2.val: #2\n temp.next = l1 #3\n l1 = l1.next #4\n else: \n temp.next = l2\n l2 = l2.next\n temp = temp.next\n temp.next = l1 or l2 #5\n return dummy.next #6\n```\n\n\nAnother way of solving is problem is by doing recursion. This is from [here](https://leetcode.com/problems/merge-two-sorted-lists/discuss/9735/Python-solutions-(iteratively-recursively-iteratively-in-place)). The first check is obvious! If one of them is empty, return the other one! Similar to line `#5` of previous solution. Here, we have two cases, whatever list has the smaller first element (equal elements also satisfies line `#1`), will be returned at the end. In the example `l1 = [1,2,4], l2 = [1,3,4]`, we go in the `if` statement of line `#1` first, this means that the first element of `l1` doesn\'t get changed! Then, we move the pointer to the second element of `l1` by calling the function again but with `l1.next` and `l2` as input! This round of call, goes to line `#2` because now we have element `1` from `l2` versus `2` from `l1`. Now, basically, `l2` gets connected to the tail of `l1`. We keep moving forward by switching between `l1` and `l2` until the last element. Sorry if it\'s not clear enough! I\'m not a fan of recursion for such a problems! But, let me know which part it\'s hard to understand, I\'ll try to explain better! \n\n```\nclass Solution:\n def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode: \n if not l1 or not l2:\n return l1 or l2\n \n if l1.val <= l2.val: #1\n l1.next = self.mergeTwoLists(l1.next, l2)\n return l1\n else: #2\n l2.next = self.mergeTwoLists(l1, l2.next)\n return l2\n```\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n===============================================================\nFinal note: Please let me know if you want me to explain anything in more detail. \n | 484 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
O( n )✅ | Python (Step by step explanation)✅ | merge-two-sorted-lists | 0 | 1 | # Intuition\n<!-- Your intuition or thoughts about solving the problem -->\nMy intuition is to merge two sorted linked lists into a single sorted linked list while keeping track of the current nodes in both input lists.\n\n# Approach\n<!-- Describe your approach to solving the problem -->\n1. Initialize a new linked list named `merged`.\n2. Initialize a temporary node `temp` pointing to `merged`.\n3. While both `l1` and `l2` are not empty:\n - Compare the values of the current nodes in `l1` and `l2`.\n - If `l1.val` is less than `l2.val`, set `temp.next` to `l1` and move `l1` to the next node.\n - If `l1.val` is greater than or equal to `l2.val`, set `temp.next` to `l2` and move `l2` to the next node.\n - Move `temp` to the next node.\n4. After the loop, if there are remaining nodes in `l1`, append them to `temp.next`.\n5. If there are remaining nodes in `l2`, append them to `temp.next`.\n6. Return the `next` node of `merged` as the merged linked list.\n\n# Complexity\n- Time complexity:\n - The while loop iterates through both linked lists, and each step involves constant-time operations.\n - The time complexity is O(n), where n is the total number of nodes in the two linked lists.\n\n- Space complexity:\n - Your code uses a constant amount of extra space for variables (`merged` and `temp`), and the space complexity is O(1).\n\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n merged = ListNode()\n temp = merged\n\n while l1 and l2 :\n if l1.val < l2.val :\n temp.next = l1\n l1 = l1.next\n else :\n temp.next = l2\n l2 = l2.next\n\n temp = temp.next\n\n if l1:\n temp.next = l1\n else :\n temp.next = l2\n\n return merged.next \n\n```\n\n# Please upvote the solution if you understood it.\n\n | 7 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Awesome Trick For Linked List----->Python3 | merge-two-sorted-lists | 0 | 1 | \n\n# Single Linked List----->Time : O(N)\n```\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n out=dummy=ListNode()\n while list1 and list2:\n if list1.val<list2.val:\n out.next=list1\n list1=list1.next\n else:\n out.next=list2\n list2=list2.next\n out=out.next\n if list1:\n out.next=list1\n list1=list1.next\n if list2:\n out.next=list2\n list2=list2.next\n return dummy.next\n\n```\n# please upvote me it would encourage me alot\n | 14 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Iterative approach | merge-two-sorted-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince the lists are already sorted iterate through both lists and add minNode to new list until we reach end of any list\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Prepare head and tail of new result list, instead of keeping this empty prefill this with None node as this will make our lifes easy by skipping null check in our implementation\n2. Run a while loop on both lists until one of them is empty\n3. Identify minNode and increment the header on that list\n4. Add this minNode to our list\n5. Once we reach the end of a list, append remaining list to end of our result list\n6. Be careful when returning head of result list, we should skip the initial dummy node\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n o(n+n) => o(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n o(n+n) => o(n)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n preHead = ListNode(None)\n tail = preHead\n while list1 and list2:\n if list1.val <= list2.val:\n minNode, list1 = list1, list1.next\n else:\n minNode, list2 = list2, list2.next\n \n tail.next = minNode\n tail = tail.next\n\n tail.next = list1 or list2\n\n return preHead.next\n``` | 0 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Python3 easy solution | merge-two-sorted-lists | 0 | 1 | # Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n dummy=ListNode()\n tail=dummy\n while list1 and list2:\n if list1.val<list2.val:\n tail.next=list1\n list1=list1.next\n else:\n tail.next=list2\n list2=list2.next\n tail=tail.next\n if list1: tail.next=list1\n elif list2: tail.next=list2\n return dummy.next\n```\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n | 1 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
✔️ Python Easy Solution | 99% Faster | Merge Two Sorted Lists | merge-two-sorted-lists | 0 | 1 | **IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE**\n\nVisit this blog to learn Python tips and techniques and to find a Leetcode solution with an explanation: https://www.python-techs.com/\n\n**Solution:**\n```\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n newHead = dummyHead = ListNode()\n while list1 and list2:\n if list1.val < list2.val:\n dummyHead.next = list1\n list1 = list1.next\n else:\n dummyHead.next = list2\n list2 = list2.next\n dummyHead = dummyHead.next\n \n if list1:\n dummyHead.next = list1\n if list2:\n dummyHead.next = list2\n return newHead.next\n```\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.** | 97 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Simplest and READABLE Python code | merge-two-sorted-lists | 0 | 1 | \n# Code\n```\nclass Solution:\n def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:\n # Create a dummy node \n dummy = ListNode(0)\n cur = dummy\n \n while l1 and l2:\n if l1.val <= l2.val:\n cur.next = l1\n l1 = l1.next\n else:\n cur.next = l2\n l2 = l2.next\n \n cur = cur.next\n \n # In case any has still nodes left, just append them\n if l1:\n cur.next = l1\n if l2:\n cur.next = l2\n \n return dummy.next\n\n``` | 1 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
python iterative method | merge-two-sorted-lists | 0 | 1 | # Intuition\nThis question is asking you to merge 2 linked lists and return the head.\n\nThink of this question like you are inserting values between the head and the tail of a new empty list.\n\nWe start off by initalizing a head and movingtail to ListNode(). This makes head and tail both equal to an empty node. the head variable is commonly used and called the "dummy node". \n\nNext we loop through both lists and compare values to see which one is greater as we must merge both lists in increasing value. i named movingtail movingtail because it moves while head stays in place. Everytime one of the linked list nodes is greater than the other the tail moves/sets the next node equal to the "greater node" (movingtail.next = l1) and the "greater node" moves to the next node in that linked list. \n\nIf either linked list is empty this runs: (movingtail.next = l1 or l2) which sets movingtail equal to the linked list that isn\'t empty. \n\nAt the end of the program head.next returns, which means that the head or dummy node\'s next value (the head) will get returned which is the answer to the question.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:\n head = movingtail = ListNode()\n \n while l1 and l2:\n if l1.val <= l2.val:\n movingtail.next = l1\n l1 = l1.next\n else:\n movingtail.next = l2\n l2 = l2.next\n movingtail = movingtail.next\n \n movingtail.next = l1 or l2\n return head.next\n``` | 6 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Python3 Iterative and Recursive | merge-two-sorted-lists | 0 | 1 | \n# Complexity\n- Time complexity: O(m + n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n- Iterative \n\n```\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n dummy = ListNode(-1)\n curr = dummy\n while list1 and list2:\n if list1.val <= list2.val:\n curr.next = list1\n list1 = list1.next\n else:\n curr.next = list2\n list2 = list2.next\n curr = curr.next\n curr.next = list1 if list1 is not None else list2\n return dummy.next\n \n```\n\n- Recursive\n\n```\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n if not list1: return list2\n if not list2: return list1\n elif list1.val < list2.val: \n list1.next = self.mergeTwoLists(list1.next, list2)\n return list1\n else: \n list2.next = self.mergeTwoLists(list1, list2.next)\n return list2\n``` | 1 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Simplest python solution beats 99% | merge-two-sorted-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n if not list1:\n return list2\n if not list2:\n return list1\n else:\n temp = ListNode()\n if list1.val > list2.val:\n temp = list2\n temp.next = self.mergeTwoLists(list1,list2.next)\n else:\n temp = list1\n temp.next = self.mergeTwoLists(list1.next,list2)\n return temp\n``` | 2 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Python Simplest Iterative Solution with Explanation | Beg to Adv | Linked List | merge-two-sorted-lists | 0 | 1 | ```python\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n dummy = ListNode(0) # making a dummy node\n curr = dummy # creating a pointer pointing to the dummy node\n \n while list1 and list2: # we must be having both list to perform merge operation.\n if list1.val < list2.val: # in case list value is less then list2,\n curr.next = list1 # then we move our pointer ahead in list 1.\n list1 = list1.next # having value of next element of list2\n else:\n curr.next = list2 # in case list2 value is greaer then list 1 value.\n list2 = list2.next #having value of next element of list2\n curr = curr.next # moving our curr pointer\n \n # In case all the elements of any one of the list is travered. then we`ll move our pointer to the left over. \n # As lists are soted already, technically we could do that\n # Method : 1\n# if list1:\n# curr.next = list1\n# elif list2:\n# curr.next = list2\n \n # Method : 2\n curr.next = list1 or list2\n \n return dummy.next # return next bcz first node is dummy. \n```\n***Found helpful, Do upvote !!*** | 13 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Python | Easy | merge-two-sorted-lists | 0 | 1 | ```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n \n ans= ListNode()\n final = ans\n while list1 and list2:\n if list1.val<list2.val:\n ans.next = list1\n list1 = list1.next\n else:\n ans.next = list2\n list2 = list2.next\n ans = ans.next\n \n if list1:\n ans.next = list1\n else:\n ans.next = list2\n \n return final.next | 1 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
21. Merge Two Sorted Lists | merge-two-sorted-lists | 0 | 1 | # Intuition\nPretty simple to understand\n\n# Approach\n1.Get elements from both Linked lists into a normal list\n2. Sort the list (List.sort(reverse=True))\n3. Then convert the new list into a linked list\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n arr=[]\n l3=None\n while list1:\n if list1 is not None:\n arr.append(list1.val)\n list1=list1.next\n \n while list2:\n if list2 is not None:\n arr.append(list2.val)\n list2=list2.next\n \n arr.sort(reverse=True) \n for i in arr:\n l3=ListNode(i,l3)\n return l3\n\n\n\n\n\n\n\n \n``` | 1 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Python Easy Solution in O(n) Complexity | merge-two-sorted-lists | 0 | 1 | ```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n list3=ListNode()\n temp1,temp2,temp=list1,list2,list3\n while temp1 and temp2:\n if temp1.val<=temp2.val:\n temp.next=temp1\n temp1=temp1.next\n else:\n temp.next=temp2\n temp2=temp2.next\n temp=temp.next\n if temp1:\n temp.next=temp1\n if temp2:\n temp.next=temp2\n return list3.next\n```\n\n**Upvote if you like the solution or ask if there is any query** | 3 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
In Place Merging in python : O(N) time O(1) space | merge-two-sorted-lists | 0 | 1 | # Intuition\nSo there are two approaches to solve the problem,\nfirst by creating a wholesome new list which is pretty easy, \nsecond by modifying the list itself \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nthis question can be solved by recursive or iterative approach\nI\'ll discuss iterative one(recursive is commented in the solution)\nSo need to maintain two pointers l1 and l2 and \nwhile l1.val < l2.val; move l1 untill the condition becomes false\nwhen we break out of the condition, what we do is we do some link changes and swap l1 and l2;\na tmp pointer is maintained for link changes\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n # def merge(l1, l2):\n # if l1.val < l2.val:\n # l1.next = merge(l1.next,l2)\n # return l1\n # else:\n # l2.next = merge(l1, l2.next)\n # return l2\n # return merge(list1, list2)\n\n if list1 == None:\n return list2\n if list2 == None:\n return list1\n if list1.val < list2.val:\n res, tmp = list1, list1\n l1 = list1.next\n l2 = list2\n else:\n res, tmp = list2, list2\n l1 = list2.next\n l2 = list1\n while l1 != None:\n while l1 and l2 and l1.val <= l2.val:\n tmp = tmp.next\n l1 = l1.next\n else:\n tmp.next = l2\n l1, l2 = l2, l1\n tmp.next = l2\n return res\n \n\n \n\n\n\n``` | 2 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Merging Two Sorted Linked List Using a Dummy Node - Algorithm Explained with Time and Space Analysis | merge-two-sorted-lists | 0 | 1 | # Intuition\nThe intuition of the solution is to iteratively compare the values of the nodes in `list1` and `list2`, and add the node with the smaller value to the resulting linked list. A dummy node is used as the starting node of the resulting linked list to make the implementation easier.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to use two pointers, `list1` and `list2`, to traverse through the two linked lists. A third pointer, current, is used to keep track of the current node in the resulting linked list. The comparison is performed in a while loop, and the node with the smaller value is added to the `current.next`, and the corresponding pointer is moved to the next node in the linked list. After one of the linked lists is exhausted, the remaining elements in the other linked list are added to the end of the resulting linked list. The head of the resulting linked list is returned by `dummy.next`.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(m + n), where m is the length of `list1` and n is the length of `list2`. This is because the solution iterates through both `list1` and `list2` once, and the while loop terminates when either of `list1` or `list2` becomes None.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this solution is O(1), as the solution uses a constant amount of additional space regardless of the length of the linked lists.\n\n# Code\n```\n# Definition for singly-linked list.\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\n\n\nclass Solution:\n def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:\n\n\n # create a dummy node as the starting node of the resulting linked list\n dummy = ListNode(0)\n # use a pointer to keep track of the current node in the resulting linked list\n\n current = dummy\n # iterate through both linked lists until one of them is exhausted\n\n while list1 and list2:\n # add the node with the smaller value to the resulting linked list\n if list1.val < list2.val:\n current.next = list1\n list1 = list1.next\n else:\n current.next = list2\n list2 = list2.next \n # move the pointer to the next node in the resulting linked list\n current = current.next \n # add the remaining elements in the linked list that is not exhausted\n\n if list1:\n current.next = list1\n if list2: \n current.next = list2\n # return the head of the resulting linked list\n return dummy.next\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n``` | 1 | You are given the heads of two sorted linked lists `list1` and `list2`.
Merge the two lists in a one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
Return _the head of the merged linked list_.
**Example 1:**
**Input:** list1 = \[1,2,4\], list2 = \[1,3,4\]
**Output:** \[1,1,2,3,4,4\]
**Example 2:**
**Input:** list1 = \[\], list2 = \[\]
**Output:** \[\]
**Example 3:**
**Input:** list1 = \[\], list2 = \[0\]
**Output:** \[0\]
**Constraints:**
* The number of nodes in both lists is in the range `[0, 50]`.
* `-100 <= Node.val <= 100`
* Both `list1` and `list2` are sorted in **non-decreasing** order. | null |
Python, Java w/ Explanation | Faster than 96% w/ Proof | Easy to Understand | generate-parentheses | 1 | 1 | 1. The idea is to add `\')\'` only after valid `\'(\'`\n2. We use two integer variables `left` & `right` to see how many `\'(\'` & `\')\'` are in the current string\n3. If `left < n` then we can add `\'(\'` to the current string\n4. If `right < left` then we can add `\')\'` to the current string\n\n**Python Code:**\n```\ndef generateParenthesis(self, n: int) -> List[str]:\n\tdef dfs(left, right, s):\n\t\tif len(s) == n * 2:\n\t\t\tres.append(s)\n\t\t\treturn \n\n\t\tif left < n:\n\t\t\tdfs(left + 1, right, s + \'(\')\n\n\t\tif right < left:\n\t\t\tdfs(left, right + 1, s + \')\')\n\n\tres = []\n\tdfs(0, 0, \'\')\n\treturn res\n```\n\nFor` n = 2`, the recursion tree will be something like this,\n```\n\t\t\t\t\t\t\t\t \t(0, 0, \'\')\n\t\t\t\t\t\t\t\t \t |\t\n\t\t\t\t\t\t\t\t\t(1, 0, \'(\') \n\t\t\t\t\t\t\t\t / \\\n\t\t\t\t\t\t\t(2, 0, \'((\') (1, 1, \'()\')\n\t\t\t\t\t\t\t / \\\n\t\t\t\t\t\t(2, 1, \'(()\') (2, 1, \'()(\')\n\t\t\t\t\t\t / \\\n\t\t\t\t\t(2, 2, \'(())\') (2, 2, \'()()\')\n\t\t\t\t\t\t |\t |\n\t\t\t\t\tres.append(\'(())\') res.append(\'()()\')\n \n```\n\n**Java Code:**\n```java\nclass Solution {\n public List<String> generateParenthesis(int n) {\n List<String> res = new ArrayList<String>();\n recurse(res, 0, 0, "", n);\n return res;\n }\n \n public void recurse(List<String> res, int left, int right, String s, int n) {\n if (s.length() == n * 2) {\n res.add(s);\n return;\n }\n \n if (left < n) {\n recurse(res, left + 1, right, s + "(", n);\n }\n \n if (right < left) {\n recurse(res, left, right + 1, s + ")", n);\n }\n }\n\t// See above tree diagram with parameters (left, right, s) for better understanding\n}\n```\n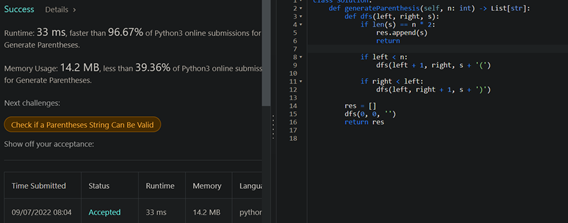\n\n\n\n\n\n\n | 1,292 | Given `n` pairs of parentheses, write a function to _generate all combinations of well-formed parentheses_.
**Example 1:**
**Input:** n = 3
**Output:** \["((()))","(()())","(())()","()(())","()()()"\]
**Example 2:**
**Input:** n = 1
**Output:** \["()"\]
**Constraints:**
* `1 <= n <= 8` | null |
Beats 92% using iteration. Detailed journey of stack explained | generate-parentheses | 0 | 1 | # Code\n```\nclass Solution:\n def generateParenthesis(self, n: int) -> List[str]:\n\n ##########################################################################\n ##########################################################################\n\n \'\'\'for n=2 amazingly explained recursion tree\n \t\t\t\t\t\t\t\t \t(0, 0, \'\')\n\t\t\t\t\t\t\t\t \t |\t\n\t\t\t\t\t\t\t\t\t(1, 0, \'(\') \n\t\t\t\t\t\t\t\t / \\\n\t\t\t\t\t\t\t(2, 0, \'((\') (1, 1, \'()\')\n\t\t\t\t\t\t\t / \\\n\t\t\t\t\t\t(2, 1, \'(()\') (2, 1, \'()(\')\n\t\t\t\t\t\t / \\\n\t\t\t\t\t(2, 2, \'(())\') (2, 2, \'()()\')\n\t\t\t\t\t\t |\t |\n\t\t\t\t\tres.append(\'(())\') res.append(\'()()\')\n \'\'\'\n ##########################################################################\n ########################################################################## \n\n \'\'\' Recusive approach code\n def dfs(left, right, s):\n if len(s) == n * 2:\n res.append(s)\n return \n\n if left < n:\n dfs(left + 1, right, s + \'(\')\n\n if right < left:\n dfs(left, right + 1, s + \')\')\n\n res = []\n dfs(0, 0, \'\')\n return res\'\'\'\n ##########################################################################\n ##########################################################################\n\n #using iteration\n\n result = []\n left = right = 0\n q = [(left, right, \'\')]\n while q:\n left, right, s = q.pop()\n if len(s) == 2 * n:\n result.append(s)\n if left < n:\n q.append((left + 1, right, s + \'(\'))\n if right < left:\n q.append((left, right + 1, s + \')\'))\n return result\n #########################################################################\n ##########################################################################\n\n #Journey of q\n \'\'\'q = [(left, right, \'\')] == [(0,0,\'\')]\n |\n left = 0 |\n right = 0 |\n s = \'\' |\n now q = [(1, 0, \'(\')]\n left = 1 |\n right = 0 | \n s = \'(\' |\n |\n right<left |\n q = [(2, 0, \'((\'), (1, 1, \'()\')]\n left = 1 |\n right =1 |\n s = \'()\' |\n |\n q = [(2, 0, \'((\'), (2, 1, \'()(\')]\n left =2 |\n right =1 |\n right<left |\n s=\'()(\' | \n q = [(2, 0, \'((\'), (3, 1, \'()((\'), (2, 2, \'()()\')]\n left =2\n right =2\n s = \'()()\'\n q = [(2, 0, \'((\'), (3, 1, \'()((\'), (3, 2, \'()()(\')]\n next iteration \n q = [(2, 0, \'((\'), (3, 1, \'()((\'), (3, 3, \'()()()\')]\n s = \'()()()\'\n result = [\'()()()\',.............]\n [\'()()()\', \'()(())\', \'(())()\', \'(()())\', \'((()))\']\'\'\'\n``` | 1 | Given `n` pairs of parentheses, write a function to _generate all combinations of well-formed parentheses_.
**Example 1:**
**Input:** n = 3
**Output:** \["((()))","(()())","(())()","()(())","()()()"\]
**Example 2:**
**Input:** n = 1
**Output:** \["()"\]
**Constraints:**
* `1 <= n <= 8` | null |
Python Iterative Solution ( Non Recursive) | generate-parentheses | 0 | 1 | \n# Code\n```\nclass Solution:\n def generateParenthesis(self, n: int) -> List[str]:\n res = [\'\']\n n1 = [0]\n n2 = [0]\n\n j = 0;\n while j < 2*n :\n rest = []\n n1t = []\n n2t = []\n for i in range(0,len(res)):\n if( n1[i] > n2[i] ):\n rest.append( res[i]+\')\' );\n n1t.append(n1[i])\n n2t.append(n2[i]+1 )\n rest.append( res[i]+\'(\' );\n n1t.append(n1[i]+1)\n n2t.append(n2[i] )\n res = rest\n n1 = n1t\n n2 = n2t \n j += 1\n\n ans = []\n for i in range(0,len(res)):\n if( n1[i] == n2[i] ):\n ans.append(res[i]);\n\n return ans ; \n \n \n``` | 2 | Given `n` pairs of parentheses, write a function to _generate all combinations of well-formed parentheses_.
**Example 1:**
**Input:** n = 3
**Output:** \["((()))","(()())","(())()","()(())","()()()"\]
**Example 2:**
**Input:** n = 1
**Output:** \["()"\]
**Constraints:**
* `1 <= n <= 8` | null |
Python3 | Recursive approach | Step by step explanation ✅✅ | generate-parentheses | 0 | 1 | # Intuition\nThe problem aims to generate valid combinations of parentheses given an integer `n`. We need to find all possible combinations of `n` pairs of open and close parentheses.\n\n# Approach\n1. Initialize an empty list `ans` to store the valid combinations of parentheses and an empty stack `stack` to help in generating these combinations.\n\n2. Define a recursive function `generator` that takes two parameters: `openp` (the count of open parentheses) and `closep` (the count of close parentheses).\n\n3. In the `generator` function, check if both `openp` and `closep` are equal to `n`. If they are, it means we have created a valid combination of parentheses, so we append the contents of the `stack` (joined as a string) to the `ans` list and return.\n\n4. Inside the `generator` function, there are two recursive calls:\n - If the count of open parentheses (`openp`) is less than `n`, we can add an open parenthesis "(" to the `stack`, increment `openp`, and make a recursive call.\n - If the count of close parentheses (`closep`) is less than `openp`, we can add a close parenthesis ")" to the `stack`, increment `closep`, and make a recursive call.\n\n5. The `generator` function explores all possible combinations of parentheses by adding either an open or a close parenthesis when valid, and it removes the added parenthesis after each recursive call to the function.\n\n6. Call the `generator` function with initial values of `openp` and `closep` both set to 0.\n\n7. Return the `ans` list, which contains all valid combinations of parentheses.\n\n# Complexity\n- Time complexity: The time complexity is O(2^(2n) * n) since there are 2^(2n) possible combinations and we spend O(n) time on each of them to check if it\'s valid and append it to the result list.\n- Space complexity: The space complexity is O(n) for the recursive call stack and O(n) for the `stack` variable, making it O(n) in total.\n\n\n# Code\n```\nclass Solution:\n def generateParenthesis(self, n: int) -> List[str]:\n ans = []\n stack = []\n\n def generator(openp , closep) :\n if openp == closep == n :\n ans.append("".join(stack))\n return\n\n if openp < n :\n stack.append("(")\n generator(openp + 1 , closep)\n stack.pop()\n\n if closep < openp :\n stack.append(")")\n generator(openp , closep+1)\n stack.pop()\n\n generator(0 , 0)\n return ans \n\n\n \n\n```\n\n# Please upvote the solution if you understood it.\n\n | 3 | Given `n` pairs of parentheses, write a function to _generate all combinations of well-formed parentheses_.
**Example 1:**
**Input:** n = 3
**Output:** \["((()))","(()())","(())()","()(())","()()()"\]
**Example 2:**
**Input:** n = 1
**Output:** \["()"\]
**Constraints:**
* `1 <= n <= 8` | null |
Python3 | Recursive approach | Simple Logic | Step by step explanation | generate-parentheses | 0 | 1 | One thing we need to understand is, we need a way to add \u201C(\u201D and \u201C)\u201D to all possible cases and \nthen find a way to validate so that we don\u2019t generate the unnecessary ones.\n\nThe first condition is if there are more than 0 open / left brackets, we recurse with the right\nones. And if we have more than 0 right brackets, we recurse with the left ones. Left and right\nare initialized with` \'n\' `- the number given.\n\n\n```\n\t\t\tif left>0:\n helper(ans, s+\'(\', left-1, right)\n \n if right>0:\n helper(ans, s+\')\', left, right-1)\n```\n\n<br>\n\nThere\u2019s a catch. We can\u2019t add the \u201C)\u201D everytime we have `right>0` cause then it will not be\nbalanced. We can balance that with a simple condition of `left<right.`\n\n```\n\t\t\tif left>0:\n helper(ans, s+\'(\', left-1, right)\n \n if right>0 and left<right:\n helper(ans, s+\')\', left, right-1)\n```\n\n<br>\nSince this is a recursive approach we need to have a **BASE condition**,\nand the base case is: \n\nWhen both right and left are 0, \nwe have found one possible combination of parentheses \n& we now need to append/add the `\'s\'` to `\'ans\'` list.\n\n```\n\t\t\tif left==0 and right==0:\n ans.append(s)\n```\n\n<br>\n<br>\n\n**Complete code**\n```\nclass Solution:\n def generateParenthesis(self, n: int) -> List[str]:\n \n \n def helper(ans, s, left, right):\n if left==0 and right==0:\n ans.append(s)\n \n if left>0:\n helper(ans, s+\'(\', left-1, right)\n \n if right>0 and left<right:\n helper(ans, s+\')\', left, right-1)\n \n ans = []\n helper(ans, \'\', n, n)\n \n return ans\n```\n\n\n\n<br>\n<br>\n*If this post seems to be helpful, please upvote!!* | 61 | Given `n` pairs of parentheses, write a function to _generate all combinations of well-formed parentheses_.
**Example 1:**
**Input:** n = 3
**Output:** \["((()))","(()())","(())()","()(())","()()()"\]
**Example 2:**
**Input:** n = 1
**Output:** \["()"\]
**Constraints:**
* `1 <= n <= 8` | null |
Beats 98% Easy to Understand | merge-k-sorted-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nfrom typing import List\n\nclass Solution:\n def mergeKLists(self, lists: List[ListNode]) -> ListNode:\n dummy = ListNode(None)\n curr = dummy\n heap = []\n\n for i, node in enumerate(lists):\n if node:\n heapq.heappush(heap, (node.val, i, node))\n lists[i] = node.next\n\n while heap:\n val, i, node = heapq.heappop(heap)\n curr.next = node\n curr = curr.next\n\n if node.next:\n heapq.heappush(heap, (node.next.val, i, node.next))\n\n return dummy.next\n\n``` | 3 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Python Simple solution | merge-k-sorted-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNot very space efficient, but pretty fast. Move everything into an array, sort the array, and move everything back into a linked list.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nUnless I\'m wrong, this should be O(KlogK).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nI\'m really not quite sure about this one, maybe O(K)?\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:\n head = tmp = ListNode()\n arr = []\n\n for l in lists:\n while l != None:\n arr.append(l.val)\n l = l.next\n\n for val in sorted(arr):\n tmp.next = ListNode()\n tmp = tmp.next\n tmp.val = val\n\n return head.next\n``` | 2 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Day 71 || Divide and Conquer || Easiest Beginner Friendly Sol | merge-k-sorted-lists | 1 | 1 | **NOTE 1 - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n**NOTE 2 - BEFORE SOLVING THIS PROBELM, I WILL HIGHLY RECOMMEND YOU TO SOLVE BELOW PROBLEM FOR BETTER UNDERSTANDING.**\n**21. Merge Two Sorted Lists :** https://leetcode.com/problems/merge-two-sorted-lists/description/ \n**SOLUTION :** https://leetcode.com/problems/merge-two-sorted-lists/solutions/3288537/o-m-n-time-and-o-1-space-easiest-beginner-friendly-solution/\n\n# Intuition of this Problem:\n**This solution uses the merge sort algorithm to merge all the linked lists in the input vector into a single sorted linked list. The merge sort algorithm works by recursively dividing the input into halves, sorting each half separately, and then merging the two sorted halves into a single sorted output.**\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem:\n1. Define a function merge that takes two pointers to linked lists as input and merges them in a sorted manner.\n - a. Create a dummy node with a value of -1 and a temporary node pointing to it.\n - b. Compare the first node of the left and right linked lists, and append the smaller one to the temporary node.\n - c. Continue this process until either of the lists becomes empty.\n - d. Append the remaining nodes of the non-empty list to the temporary node.\n - e. Return the next node of the dummy node.\n\n1. Define a function mergeSort that takes three arguments - a vector of linked lists, a starting index, and an ending index. It performs merge sort on the linked lists from the starting index to the ending index.\n - a. If the starting index is equal to the ending index, return the linked list at that index.\n - b. Calculate the mid index and call mergeSort recursively on the left and right halves of the vector.\n - c. Merge the two sorted linked lists obtained from the recursive calls using the merge function and return the result.\n\n1. Define the main function mergeKLists that takes the vector of linked lists as input and returns a single sorted linked list.\n - a. If the input vector is empty, return a null pointer.\n - b. Call the mergeSort function on the entire input vector, from index 0 to index k-1, where k is the size of the input vector.\n - c. Return the merged linked list obtained from the mergeSort function call.\n1. End of algorithm.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* merge(ListNode *left, ListNode *right) {\n ListNode *dummy = new ListNode(-1);\n ListNode *temp = dummy;\n while (left != nullptr && right != nullptr) {\n if (left -> val < right -> val) {\n temp -> next = left;\n temp = temp -> next;\n left = left -> next;\n }\n else {\n temp -> next = right;\n temp = temp -> next;\n right = right -> next;\n }\n }\n while (left != nullptr) {\n temp -> next = left;\n temp = temp -> next;\n left = left -> next;\n }\n while (right != nullptr) {\n temp -> next = right;\n temp = temp -> next;\n right = right -> next;\n }\n return dummy -> next;\n }\n ListNode* mergeSort(vector<ListNode*>& lists, int start, int end) {\n if (start == end) \n return lists[start];\n int mid = start + (end - start) / 2;\n ListNode *left = mergeSort(lists, start, mid);\n ListNode *right = mergeSort(lists, mid + 1, end);\n return merge(left, right);\n }\n ListNode* mergeKLists(vector<ListNode*>& lists) {\n if (lists.size() == 0)\n return nullptr;\n return mergeSort(lists, 0, lists.size() - 1);\n }\n};\n```\n```Java []\nclass Solution {\n public ListNode merge(ListNode left, ListNode right) {\n ListNode dummy = new ListNode(-1);\n ListNode temp = dummy;\n while (left != null && right != null) {\n if (left.val < right.val) {\n temp.next = left;\n temp = temp.next;\n left = left.next;\n } else {\n temp.next = right;\n temp = temp.next;\n right = right.next;\n }\n }\n while (left != null) {\n temp.next = left;\n temp = temp.next;\n left = left.next;\n }\n while (right != null) {\n temp.next = right;\n temp = temp.next;\n right = right.next;\n }\n return dummy.next;\n }\n \n public ListNode mergeSort(List<ListNode> lists, int start, int end) {\n if (start == end) {\n return lists.get(start);\n }\n int mid = start + (end - start) / 2;\n ListNode left = mergeSort(lists, start, mid);\n ListNode right = mergeSort(lists, mid + 1, end);\n return merge(left, right);\n }\n \n public ListNode mergeKLists(List<ListNode> lists) {\n if (lists.size() == 0) {\n return null;\n }\n return mergeSort(lists, 0, lists.size() - 1);\n }\n}\n\n```\n```Python []\nclass Solution:\n def merge(self, left: ListNode, right: ListNode) -> ListNode:\n dummy = ListNode(-1)\n temp = dummy\n while left and right:\n if left.val < right.val:\n temp.next = left\n temp = temp.next\n left = left.next\n else:\n temp.next = right\n temp = temp.next\n right = right.next\n while left:\n temp.next = left\n temp = temp.next\n left = left.next\n while right:\n temp.next = right\n temp = temp.next\n right = right.next\n return dummy.next\n \n def mergeSort(self, lists: List[ListNode], start: int, end: int) -> ListNode:\n if start == end:\n return lists[start]\n mid = start + (end - start) // 2\n left = self.mergeSort(lists, start, mid)\n right = self.mergeSort(lists, mid + 1, end)\n return self.merge(left, right)\n \n def mergeKLists(self, lists: List[ListNode]) -> ListNode:\n if not lists:\n return None\n return self.mergeSort(lists, 0, len(lists) - 1)\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(N log k)**, where N is the total number of nodes in all the linked lists, and k is the number of linked lists in the input vector. This is because the merge sort algorithm requires O(N log N) time to sort N items, and in this case, N is the total number of nodes in all the linked lists. The number of levels in the recursion tree of the merge sort algorithm is log k, where k is the number of linked lists in the input vector. Each level of the recursion tree requires O(N) time to merge the sorted lists, so the total time complexity is O(N log k).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(log k)**, which is the maximum depth of the recursion tree of the merge sort algorithm. The space used by each recursive call is constant, so the total space used by the algorithm is proportional to the maximum depth of the recursion tree. Since the depth of the tree is log k, the space complexity of the algorithm is O(log k).\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 65 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Easy python solution | merge-k-sorted-lists | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n extracting nodevalues in nodes list and sorting them back then after putting them in linked lists.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Consider upvoting if found helpful\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:\n nodes=[]\n head=point=ListNode(0)\n for l in lists:\n while l:\n nodes.append(l.val)\n l=l.next\n \n for x in sorted(nodes):\n point.next=ListNode(x)\n point=point.next\n return head.next\n``` | 2 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
[Python] Easy Intuitive approach | merge-k-sorted-lists | 0 | 1 | # Intuition\nSince the constraints were:\n* length of lists, $$k = 10^4$$\n* length of each linked lists say $$n = 500$$\n \nIt was not a difficult choice to go for time complexity of $$O(kn)$$ \n\nAs we will get a TLE in python (generally) if we try to exceed $$O(10^8)$$.\nBut our solution takes $$O(10^4 * 500) < O(10^8)$$\n\n\n\n# Approach\n1. We will iterate through the lists and use the first element of each linked list to find the minimum among them, which will take $$O(k)$$ as length of list is $$k$$.\n2. We will follow step 1 till all the linked lists are completely explored. We will be able to do it in $$O(n)$$ time as length of any listed list is upper bounded by $$n$$.\n\n# Complexity\n- Time complexity: $$O(kn)$$ as both step 1 and step 2 are performed simultaneously.\n\n- Space complexity: $$O(n)$$ to create a new linked list whose length is upper bounded by n.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\nclass Solution:\n def mergeKLists(self, lists: List[ListNode]) -> ListNode:\n \n l = ListNode() # the new list that we want to return\n t = l # taking a temporary copy of the new list as we need to move to next pointers to store data.\n\n # get the minimum front value of all linked lists in the input list.\n def get_min():\n min_val, min_indx = float(\'inf\'), -1\n for i in range(len(lists)):\n if lists[i] != None and lists[i].val < min_val:\n min_val = lists[i].val\n min_indx = i\n if min_indx != -1:\n # when a min value is found, \n # increment the linked list \n # so that we don\'t consider the same min value the next time \n # and also the next value of linked list comes at the front\n lists[min_indx] = lists[min_indx].next\n return min_val\n \n while(1):\n x = get_min() # get the mim value to add to new list\n if (x == float(\'inf\')): \n # if min value is not obtained that means all the linked lists are traversed so break\n break\n c = ListNode(val=x)\n t.next = c\n t = t.next\n return l.next # as we made l to be just a head for our actual linked list\n \n\n\n\n\n \n\n\n``` | 7 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |
Python3 and C++ || 95 ms || Beats 95.60% and EASY | merge-k-sorted-lists | 0 | 1 | # Please UPVOTE\uD83D\uDE0A\n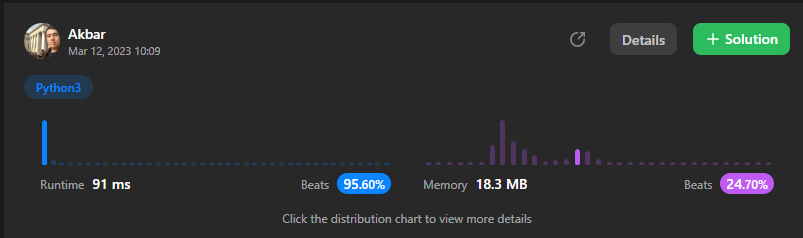\n\n\n# Python3\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:\n v=[]\n for i in lists:\n x=i\n while x:\n v+=[x.val]\n x=x.next\n v=sorted(v,reverse=True)\n ans=None\n for i in v:\n ans=ListNode(i,ans)\n return ans\n```\n# C++\n```\nclass Solution {\npublic:\n ListNode* mergeKLists(vector<ListNode*>& lists) {\n vector<int>v;\n for(int i=0;i<lists.size();i++){\n while(lists[i]){\n v.push_back(lists[i]->val);\n lists[i]=lists[i]->next;\n }\n }\n sort(rbegin(v),rend(v));\n ListNode* ans=nullptr;\n for(int i=0;i<v.size();i++){\n ans=new ListNode(v[i],ans);\n }\n return ans;\n }\n};\n``` | 33 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = \[\[1,4,5\],\[1,3,4\],\[2,6\]\]
**Output:** \[1,1,2,3,4,4,5,6\]
**Explanation:** The linked-lists are:
\[
1->4->5,
1->3->4,
2->6
\]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = \[\]
**Output:** \[\]
**Example 3:**
**Input:** lists = \[\[\]\]
**Output:** \[\]
**Constraints:**
* `k == lists.length`
* `0 <= k <= 104`
* `0 <= lists[i].length <= 500`
* `-104 <= lists[i][j] <= 104`
* `lists[i]` is sorted in **ascending order**.
* The sum of `lists[i].length` will not exceed `104`. | null |