title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
✅3 Method's || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | two-sum | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe Two Sum problem asks us to find two numbers in an array that sum up to a given target value. We need to return the indices of these two numbers.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. One brute force approach is to consider every pair of elements and check if their sum equals the target. This can be done using nested loops, where the outer loop iterates from the first element to the second-to-last element, and the inner loop iterates from the next element to the last element. However, this approach has a time complexity of O(n^2).\n2. A more efficient approach is to use a hash table (unordered_map in C++). We can iterate through the array once, and for each element, check if the target minus the current element exists in the hash table. If it does, we have found a valid pair of numbers. If not, we add the current element to the hash table.\n\n**Approach using a hash table:**\n1. Create an empty hash table to store elements and their indices.\n2. Iterate through the array from left to right.\n3. For each element nums[i], calculate the complement by subtracting it from the target: complement = target - nums[i].\n4. Check if the complement exists in the hash table. If it does, we have found a solution.\n5. If the complement does not exist in the hash table, add the current element nums[i] to the hash table with its index as the value.\n6. Repeat steps 3-5 until we find a solution or reach the end of the array.\n7. If no solution is found, return an empty array or an appropriate indicator.\n\nThis approach has a time complexity of O(n) since hash table lookups take constant time on average. It allows us to solve the Two Sum problem efficiently by making just one pass through the array.\n\n# Code\n# Solution 1: (Brute Force)\n```C++ []\nclass Solution {\npublic:\n vector<int> twoSum(vector<int>& nums, int target) {\n int n = nums.size();\n for (int i = 0; i < n - 1; i++) {\n for (int j = i + 1; j < n; j++) {\n if (nums[i] + nums[j] == target) {\n return {i, j};\n }\n }\n }\n return {}; // No solution found\n }\n};\n\n```\n```Java []\nclass Solution {\n public int[] twoSum(int[] nums, int target) {\n int n = nums.length;\n for (int i = 0; i < n - 1; i++) {\n for (int j = i + 1; j < n; j++) {\n if (nums[i] + nums[j] == target) {\n return new int[]{i, j};\n }\n }\n }\n return new int[]{}; // No solution found\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n n = len(nums)\n for i in range(n - 1):\n for j in range(i + 1, n):\n if nums[i] + nums[j] == target:\n return [i, j]\n return [] # No solution found\n\n```\n\n# Solution 2: (Two-pass Hash Table)\n```C++ []\nclass Solution {\npublic:\n vector<int> twoSum(vector<int>& nums, int target) {\n unordered_map<int, int> numMap;\n int n = nums.size();\n\n // Build the hash table\n for (int i = 0; i < n; i++) {\n numMap[nums[i]] = i;\n }\n\n // Find the complement\n for (int i = 0; i < n; i++) {\n int complement = target - nums[i];\n if (numMap.count(complement) && numMap[complement] != i) {\n return {i, numMap[complement]};\n }\n }\n\n return {}; // No solution found\n }\n};\n\n```\n```Java []\nclass Solution {\n public int[] twoSum(int[] nums, int target) {\n Map<Integer, Integer> numMap = new HashMap<>();\n int n = nums.length;\n\n // Build the hash table\n for (int i = 0; i < n; i++) {\n numMap.put(nums[i], i);\n }\n\n // Find the complement\n for (int i = 0; i < n; i++) {\n int complement = target - nums[i];\n if (numMap.containsKey(complement) && numMap.get(complement) != i) {\n return new int[]{i, numMap.get(complement)};\n }\n }\n\n return new int[]{}; // No solution found\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n numMap = {}\n n = len(nums)\n\n # Build the hash table\n for i in range(n):\n numMap[nums[i]] = i\n\n # Find the complement\n for i in range(n):\n complement = target - nums[i]\n if complement in numMap and numMap[complement] != i:\n return [i, numMap[complement]]\n\n return [] # No solution found\n\n```\n# Solution 3: (One-pass Hash Table)\n```C++ []\nclass Solution {\npublic:\n vector<int> twoSum(vector<int>& nums, int target) {\n unordered_map<int, int> numMap;\n int n = nums.size();\n\n for (int i = 0; i < n; i++) {\n int complement = target - nums[i];\n if (numMap.count(complement)) {\n return {numMap[complement], i};\n }\n numMap[nums[i]] = i;\n }\n\n return {}; // No solution found\n }\n};\n\n```\n```Java []\nclass Solution {\n public int[] twoSum(int[] nums, int target) {\n Map<Integer, Integer> numMap = new HashMap<>();\n int n = nums.length;\n\n for (int i = 0; i < n; i++) {\n int complement = target - nums[i];\n if (numMap.containsKey(complement)) {\n return new int[]{numMap.get(complement), i};\n }\n numMap.put(nums[i], i);\n }\n\n return new int[]{}; // No solution found\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n numMap = {}\n n = len(nums)\n\n for i in range(n):\n complement = target - nums[i]\n if complement in numMap:\n return [numMap[complement], i]\n numMap[nums[i]] = i\n\n return [] # No solution found\n\n```\n\n\n**If you are a beginner solve these problems which makes concepts clear for future coding:**\n1. [Two Sum](https://leetcode.com/problems/two-sum/solutions/3619262/3-method-s-c-java-python-beginner-friendly/)\n2. [Roman to Integer](https://leetcode.com/problems/roman-to-integer/solutions/3651672/best-method-c-java-python-beginner-friendly/)\n3. [Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/3651712/2-method-s-c-java-python-beginner-friendly/)\n4. [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/solutions/3666304/beats-100-c-java-python-beginner-friendly/)\n5. [Remove Element](https://leetcode.com/problems/remove-element/solutions/3670940/best-100-c-java-python-beginner-friendly/)\n6. [Contains Duplicate](https://leetcode.com/problems/contains-duplicate/solutions/3672475/4-method-s-c-java-python-beginner-friendly/)\n7. [Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solutions/3675747/beats-100-c-java-python-beginner-friendly/)\n8. [Majority Element](https://leetcode.com/problems/majority-element/solutions/3676530/3-methods-beats-100-c-java-python-beginner-friendly/)\n9. [Remove Duplicates from Sorted Array](https://leetcode.com/problems/remove-duplicates-from-sorted-array/solutions/3676877/best-method-100-c-java-python-beginner-friendly/)\n10. **Practice them in a row for better understanding and please Upvote for more questions.**\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n | 3,674 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Hash Table Concept-->Python3 | two-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n dict={}\n for i,n in enumerate(nums):\n if n in dict:\n return dict[n],i\n else:\n dict[target-n]=i\n #please upvote me it would encourage me alot\n\n``` | 263 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Sum MegaPost - Python3 Solution with a detailed explanation | two-sum | 0 | 1 | If you\'re a newbie and sometimes have a hard time understanding the logic. Don\'t worry, you\'ll catch up after a month of doing Leetcode on a daily basis. Try to do it, even one example per day. It\'d help. I\'ve compiled a bunch on `sum` problems here, go ahead and check it out. Also, I think focusing on a subject and do 3-4 problems would help to get the idea behind solution since they mostly follow the same logic. Of course there are other ways to solve each problems but I try to be as uniform as possible. Good luck. \n\nIn general, `sum` problems can be categorized into two categories: 1) there is any array and you add some numbers to get to (or close to) a `target`, or 2) you need to return indices of numbers that sum up to a (or close to) a `target` value. Note that when the problem is looking for a indices, `sort`ing the array is probably NOT a good idea. \n\n\n **[Two Sum:](https://leetcode.com/problems/two-sum/)** \n \n This is the second type of the problems where we\'re looking for indices, so sorting is not necessary. What you\'d want to do is to go over the array, and try to find two integers that sum up to a `target` value. Most of the times, in such a problem, using dictionary (hastable) helps. You try to keep track of you\'ve observations in a dictionary and use it once you get to the results. \n\nNote: try to be comfortable to use `enumerate` as it\'s sometime out of comfort zone for newbies. `enumerate` comes handy in a lot of problems (I mean if you want to have a cleaner code of course). If I had to choose three built in functions/methods that I wasn\'t comfortable with at the start and have found them super helpful, I\'d probably say `enumerate`, `zip` and `set`. \n \nSolution: In this problem, you initialize a dictionary (`seen`). This dictionary will keep track of numbers (as `key`) and indices (as `value`). So, you go over your array (line `#1`) using `enumerate` that gives you both index and value of elements in array. As an example, let\'s do `nums = [2,3,1]` and `target = 3`. Let\'s say you\'re at index `i = 0` and `value = 2`, ok? you need to find `value = 1` to finish the problem, meaning, `target - 2 = 1`. 1 here is the `remaining`. Since `remaining + value = target`, you\'re done once you found it, right? So when going through the array, you calculate the `remaining` and check to see whether `remaining` is in the `seen` dictionary (line `#3`). If it is, you\'re done! you\'re current number and the remaining from `seen` would give you the output (line `#4`). Otherwise, you add your current number to the dictionary (line `#5`) since it\'s going to be a `remaining` for (probably) a number you\'ll see in the future assuming that there is at least one instance of answer. \n \n \n ```\n class Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n seen = {}\n for i, value in enumerate(nums): #1\n remaining = target - nums[i] #2\n \n if remaining in seen: #3\n return [i, seen[remaining]] #4\n else:\n seen[value] = i #5\n```\n \n \n\n **[Two Sum II:](https://leetcode.com/problems/two-sum-ii-input-array-is-sorted/)** \n\nFor this, you can do exactly as the previous. The only change I made below was to change the order of line `#4`. In the previous example, the order didn\'t matter. But, here the problem asks for asending order and since the values/indicess in `seen` has always lower indices than your current number, it should come first. Also, note that the problem says it\'s not zero based, meaning that indices don\'t start from zero, that\'s why I added 1 to both of them. \n\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n \n seen = {}\n for i, value in enumerate(numbers): \n remaining = target - numbers[i] \n \n if remaining in seen: \n return [seen[remaining]+1, i+1] #4\n else:\n seen[value] = i \n```\n\nAnother approach to solve this problem (probably what Leetcode is looking for) is to treat it as first category of problems. Since the array is already sorted, this works. You see the following approach in a lot of problems. What you want to do is to have two pointer (if it was 3sum, you\'d need three pointers as you\'ll see in the future examples). One pointer move from `left` and one from `right`. Let\'s say you `numbers = [1,3,6,9]` and your `target = 10`. Now, `left` points to 1 at first, and `right` points to 9. There are three possibilities. If you sum numbers that `left` and `right` are pointing at, you get `temp_sum` (line `#1`). If `temp_sum` is your target, you\'r done! You\'re return it (line `#9`). If it\'s more than your `target`, it means that `right` is poiting to a very large value (line `#5`) and you need to bring it a little bit to the left to a smaller (r maybe equal) value (line `#6`) by adding one to the index . If the `temp_sum` is less than `target` (line `#7`), then you need to move your `left` to a little bit larger value by adding one to the index (line `#9`). This way, you try to narrow down the range in which you\'re looking at and will eventually find a couple of number that sum to `target`, then, you\'ll return this in line `#9`. In this problem, since it says there is only one solution, nothing extra is necessary. However, when a problem asks to return all combinations that sum to `target`, you can\'t simply return the first instace and you need to collect all the possibilities and return the list altogether (you\'ll see something like this in the next example). \n\n```\nclass Solution:\n def twoSum(self, numbers: List[int], target: int) -> List[int]:\n \n for left in range(len(numbers) -1): #1\n right = len(numbers) - 1 #2\n while left < right: #3\n temp_sum = numbers[left] + numbers[right] #4\n if temp_sum > target: #5\n right -= 1 #6\n elif temp_sum < target: #7\n left +=1 #8\n else:\n return [left+1, right+1] #9\n```\n\n\n\n\n[**3Sum**](https://leetcode.com/problems/3sum/)\n\nThis is similar to the previous example except that it\'s looking for three numbers. There are some minor differences in the problem statement. It\'s looking for all combinations (not just one) of solutions returned as a list. And second, it\'s looking for unique combination, repeatation is not allowed. \n\nHere, instead of looping (line `#1`) to `len(nums) -1`, we loop to `len(nums) -2` since we\'re looking for three numbers. Since we\'re returning values, `sort` would be a good idea. Otherwise, if the `nums` is not sorted, you cannot reducing `right` pointer or increasing `left` pointer easily, makes sense? \n\nSo, first you `sort` the array and define `res = []` to collect your outputs. In line `#2`, we check wether two consecutive elements are equal or not because if they are, we don\'t want them (solutions need to be unique) and will skip to the next set of numbers. Also, there is an additional constrain in this line that `i > 0`. This is added to take care of cases like `nums = [1,1,1]` and `target = 3`. If we didn\'t have `i > 0`, then we\'d skip the only correct solution and would return `[]` as our answer which is wrong (correct answer is `[[1,1,1]]`. \n\nWe define two additional pointers this time, `left = i + 1` and `right = len(nums) - 1`. For example, if `nums = [-2,-1,0,1,2]`, all the points in the case of `i=1` are looking at: `i` at `-1`, `left` at `0` and `right` at `2`. We then check `temp` variable similar to the previous example. There is only one change with respect to the previous example here between lines `#5` and `#10`. If we have the `temp = target`, we obviously add this set to the `res` in line `#5`, right? However, we\'re not done yet. For a fixed `i`, we still need to check and see whether there are other combinations by just changing `left` and `right` pointers. That\'s what we are doing in lines `#6, 7, 8`. If we still have the condition of `left < right` and `nums[left]` and the number to the right of it are not the same, we move `left` one index to right (line `#6`). Similarly, if `nums[right]` and the value to left of it is not the same, we move `right` one index to left. This way for a fixed `i`, we get rid of repeative cases. For example, if `nums = [-3, 1,1, 3,5]` and `target = 3`, one we get the first `[-3,1,5]`, `left = 1`, but, `nums[2]` is also 1 which we don\'t want the `left` variable to look at it simply because it\'d again return `[-3,1,5]`, right? So, we move `left` one index. Finally, if the repeating elements don\'t exists, lines `#6` to `#8` won\'t get activated. In this case we still need to move forward by adding 1 to `left` and extracting 1 from `right` (lines `#9, 10`). \n\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n \n nums.sort()\n res = []\n\n for i in range(len(nums) -2): #1\n if i > 0 and nums[i] == nums[i-1]: #2\n continue\n left = i + 1 #3\n right = len(nums) - 1 #4\n \n while left < right: \n temp = nums[i] + nums[left] + nums[right]\n \n if temp > 0:\n right -= 1\n \n elif temp < 0:\n left += 1\n \n else:\n res.append([nums[i], nums[left], nums[right]]) #5\n while left < right and nums[left] == nums[left + 1]: #6\n left += 1\n while left < right and nums[right] == nums[right-1]:#7\n right -= 1 #8\n \n right -= 1 #9 \n left += 1 #10\n \n```\n\nAnother way to solve this problem is to change it into a two sum problem. Instead of finding `a+b+c = 0`, you can find `a+b = -c` where we want to find two numbers `a` and `b` that are equal to `-c`, right? This is similar to the first problem. Remember if you wanted to use the exact same as the first code, it\'d return indices and not numbers. Also, we need to re-arrage this problem in a way that we have `nums` and `target`. This code is not a good code and can be optimipized but you got the idea. For a better version of this, check [this](https://leetcode.com/problems/3sum/discuss/7384/My-Python-solution-based-on-2-sum-200-ms-beat-93.37). \n\n```\nclass Solution:\n def threeSum(self, nums: List[int]) -> List[List[int]]:\n res = []\n nums.sort()\n \n for i in range(len(nums)-2):\n if i > 0 and nums[i] == nums[i-1]:\n continue\n output_2sum = self.twoSum(nums[i+1:], -nums[i])\n if output_2sum ==[]:\n continue\n else:\n for idx in output_2sum:\n instance = idx+[nums[i]]\n res.append(instance)\n \n output = []\n for idx in res:\n if idx not in output:\n output.append(idx)\n \n \n return output\n \n \n def twoSum(self, nums, target):\n seen = {}\n res = []\n for i, value in enumerate(nums): #1\n remaining = target - nums[i] #2\n \n if remaining in seen: #3\n res.append([value, remaining]) #4\n else:\n seen[value] = i #5\n \n return res\n```\n\n[**4Sum**](https://leetcode.com/problems/4sum/)\n\nYou should have gotten the idea, and what you\'ve seen so far can be generalized to `nSum`. Here, I write the generic code using the same ideas as before. What I\'ll do is to break down each case to a `2Sum II` problem, and solve them recursively using the approach in `2Sum II` example above. \n\nFirst sort `nums`, then I\'m using two extra functions, `helper` and `twoSum`. The `twoSum` is similar to the `2sum II` example with some modifications. It doesn\'t return the first instance of results, it check every possible combinations and return all of them now. Basically, now it\'s more similar to the `3Sum` solution. Understanding this function shouldn\'t be difficult as it\'s very similar to `3Sum`. As for `helper` function, it first tries to check for cases that don\'t work (line `#1`). And later, if the `N` we need to sum to get to a `target` is 2 (line `#2`), then runs the `twoSum` function. For the more than two numbers, it recursively breaks them down to two sum (line `#3`). There are some cases like line `#4` that we don\'t need to proceed with the algorithm anymore and we can `break`. These cases include if multiplying the lowest number in the list by `N` is more than `target`. Since its sorted array, if this happens, we can\'t find any result. Also, if the largest array (`nums[-1]`) multiplied by `N` would be less than `target`, we can\'t find any solution. So, `break`. \n\n\nFor other cases, we run the `helper` function again with new inputs, and we keep doing it until we get to `N=2` in which we use `twoSum` function, and add the results to get the final output. \n\n```\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n nums.sort()\n results = []\n self.helper(nums, target, 4, [], results)\n return results\n \n def helper(self, nums, target, N, res, results):\n \n if len(nums) < N or N < 2: #1\n return\n if N == 2: #2\n output_2sum = self.twoSum(nums, target)\n if output_2sum != []:\n for idx in output_2sum:\n results.append(res + idx)\n \n else: \n for i in range(len(nums) -N +1): #3\n if nums[i]*N > target or nums[-1]*N < target: #4\n break\n if i == 0 or i > 0 and nums[i-1] != nums[i]: #5\n self.helper(nums[i+1:], target-nums[i], N-1, res + [nums[i]], results)\n \n \n def twoSum(self, nums: List[int], target: int) -> List[int]:\n res = []\n left = 0\n right = len(nums) - 1 \n while left < right: \n temp_sum = nums[left] + nums[right] \n\n if temp_sum == target:\n res.append([nums[left], nums[right]])\n right -= 1\n left += 1\n while left < right and nums[left] == nums[left - 1]:\n left += 1\n while right > left and nums[right] == nums[right + 1]:\n right -= 1\n \n elif temp_sum < target: \n left +=1 \n else: \n right -= 1\n \n return res\n```\n[**Combination Sum II**](https://leetcode.com/problems/combination-sum-ii/)\nI don\'t post combination sum here since it\'s basically this problem a little bit easier. \nCombination questions can be solved with `dfs` most of the time. if you want to fully understand this concept and [backtracking](https://www.***.org/backtracking-introduction/), try to finish [this](https://leetcode.com/problems/combination-sum/discuss/429538/General-Backtracking-questions-solutions-in-Python-for-reference-%3A) post and do all the examples. \n\nRead my older post first [here](https://leetcode.com/problems/combinations/discuss/729397/python3-solution-with-detailed-explanation). This should give you a better idea of what\'s going on. The solution here also follow the exact same format except for some minor changes. I first made a minor change in the `dfs` function where it doesn\'t need the `index` parameter anymore. This is taken care of by `candidates[i+1:]` in line `#3`. Note that we had `candidates` here in the previous post. \n\n```\nclass Solution(object):\n def combinationSum2(self, candidates, target):\n """\n :type candidates: List[int]\n :type target: int\n :rtype: List[List[int]]\n """\n res = []\n candidates.sort()\n self.dfs(candidates, target, [], res)\n return res\n \n \n def dfs(self, candidates, target, path, res):\n if target < 0:\n return\n \n if target == 0:\n res.append(path)\n return res\n \n for i in range(len(candidates)):\n if i > 0 and candidates[i] == candidates[i-1]: #1\n continue #2\n self.dfs(candidates[i+1:], target - candidates[i], path+[candidates[i]], res) #3\n```\n\n\nThe only differences are lines `#1, 2, 3`. The difference in problem statement in this one and `combinations` problem of my previous post is >>>candidates must be used once<<< and lines `#1` and `2` are here to take care of this. Line `#1` has two components where first `i > 0` and second `candidates[i] == candidates[i-1]`. The second component `candidates[i] == candidates[i-1]` is to take care of duplicates in the `candidates` variable as was instructed in the problem statement. Basically, if the next number in `candidates` is the same as the previous one, it means that it has already been taken care of, so `continue`. The first component takes care of cases like an input `candidates = [1]` with `target = 1` (try to remove this component and submit your solution. You\'ll see what I mean). The rest is similar to the previous [post](https://leetcode.com/problems/combinations/discuss/729397/python3-solution-with-detailed-explanation)\n\n================================================================\nFinal note: Please let me know if you found any typo/error/ect. I\'ll try to fix them. | 1,045 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
[VIDEO] Visualization of O(n) Solution Using a Hash Table | two-sum | 0 | 1 | https://www.youtube.com/watch?v=luicuNOBTAI\n\nInstead of checking every single combination of pairs, the key realization is that for each number in the array, there is only **one** number that can be added to it to reach the target.\n\nWe combine this with a hash table, which can look up values in constant time, to keep track of array elements and its indices as we traverse it. For each array element **x**, we calculate **target - x** and check if we\'ve encountered it in the array before. If we have, then we immediately return the index stored in the hash table and the index of the current element we\'re on.\n\nIn the worst case, the array will only have to be traversed once, resulting in an O(n) solution.\n\n# Code\n```\nclass Solution(object):\n def twoSum(self, nums, target):\n seen = {}\n for i in range(len(nums)):\n diff = target - nums[i]\n if diff in seen:\n return [seen[diff], i]\n else:\n seen[nums[i]] = i\n``` | 4 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
1. (Solution) | two-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is a Brute Force Method\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSubtract the target from the list of element from the starting and find the second number. After that search that second number in the list. if the second number exist in the list then append index in the list i.e index of the first number and the second number.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n n = len(nums)\n\n for i in range (n):\n sec_number = target - nums[i]\n \n for j in range (i+1, n):\n if sec_number == nums[j]:\n\n return [i,j]\n # result_list = []\n # sum = 0 \n # k = 2\n # n = len(nums)\n\n # for i in range (k):\n # sum = sum + nums[i]\n\n # if sum == target:\n # return [0, 1]\n\n # else:\n # for i in range (k, n):\n # sum = sum + nums[i] - nums[i-k]\n # if sum == target:\n # result_list.append(i-1)\n # result_list.append(i)\n # return result_list\n\n``` | 2 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Solutions in C++ and Python3 | For Loop | two-sum | 0 | 1 | \n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> twoSum(vector<int>& nums, int target) {\n vector<int>answer;\n for (int i = 0; i < nums.size(); i++){\n for (int j = i + 1; j < nums.size(); j++){\n if (nums.at(i) + nums.at(j) == target){answer.push_back(i); answer.push_back(j); break;}\n }\n }\n return answer;\n }\n};\n```\n```Python []\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n answer = []\n for first in range(len(nums)):\n for second in range(first + 1, len(nums)):\n if nums[first] + nums[second] == target:\n answer.append(first)\n answer.append(second)\n break\n return answer\n```\n\n | 2 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Binbin's very simple solution! dont understand why so many solutions used user.out........> < | two-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n pre = []\n for i in range(len(nums)):\n int2 = nums[i]\n int1 = target - int2\n if int1 not in pre:\n pre.append(int2)\n else:\n return [i,pre.index(int1)]\n \n\n\n\n``` | 1 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
✅98.21%🔥HashMap & Time complexity🔥1 line Code 🔥 | two-sum | 1 | 1 | # Problem\n#### The problem statement describes a classic coding interview question. You are given an array of integers (nums) and an integer (target). Your task is to find two distinct numbers in the array that add up to the target. You need to return the indices of these two numbers.\n\n---\n# Solution\n\n##### 1. The twoSum function takes two arguments: nums, which is the list of integers, and target, which is the desired sum.\n\n##### 2. The solution uses a nested loop. The outer loop iterates through the elements of the nums list using enumerate. The outer loop variable i represents the index, and x represents the element at that index.\n\n##### 3.The inner loop also uses enumerate but starts from the i+1 index. This ensures that you don\'t use the same element twice (as the problem specifies). The inner loop variable j represents the index, and y represents the element at that index.\n\n##### 4.The condition if x + y == target checks whether the sum of the current elements x and y is equal to the target.\n\n##### 5.If a pair of elements is found that satisfies the condition, the next function returns a tuple (i, j) representing the indices of the two elements that add up to the target.\n---\n\n# Code\n```Python3 []\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n return next((i, j) for i, x in enumerate(nums) for j, y in enumerate(nums[i+1:], i+1) if x + y == target)\n\n```\n```python []\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n return next((i, j) for i, x in enumerate(nums) for j, y in enumerate(nums[i+1:], i+1) if x + y == target)\n\n```\n```C# []\npublic class Solution\n{\n public int[] TwoSum(int[] nums, int target)\n {\n for (int i = 0; i < nums.Length; i++)\n {\n for (int j = i + 1; j < nums.Length; j++)\n {\n if (nums[i] + nums[j] == target)\n {\n return new int[] { i, j };\n }\n }\n }\n throw new ArgumentException("No solution found");\n }\n}\n\n```\n```javascript []\nvar twoSum = function(nums, target) {\n const numToIndex = new Map(); // Create a Map to store numbers and their indices\n\n for (let i = 0; i < nums.length; i++) {\n const complement = target - nums[i];\n\n // Check if the complement exists in the Map\n if (numToIndex.has(complement)) {\n return [numToIndex.get(complement), i];\n }\n\n // Store the current number and its index in the Map\n numToIndex.set(nums[i], i);\n }\n\n throw new Error("No solution found");\n};\n```\n```C []\nint* twoSum(int* nums, int numsSize, int target, int* returnSize) {\n int* result = (int*)malloc(2 * sizeof(int)); // Allocate memory for the result array\n if (result == NULL) {\n *returnSize = 0;\n return NULL; // Return NULL if memory allocation fails\n }\n\n for (int i = 0; i < numsSize; i++) {\n for (int j = i + 1; j < numsSize; j++) {\n if (nums[i] + nums[j] == target) {\n result[0] = i;\n result[1] = j;\n *returnSize = 2; // Set the return size to 2\n return result; // Return the result array\n }\n }\n }\n\n *returnSize = 0; // If no solution found, set return size to 0\n free(result); // Free the allocated memory before returning NULL\n return NULL; // Return NULL if no solution is found\n}\n```\n```Java []\npublic class Solution {\n public int[] twoSum(int[] nums, int target) {\n Map<Integer, Integer> numToIndex = new HashMap<>();\n for (int i = 0; i < nums.length; i++) {\n int complement = target - nums[i];\n if (numToIndex.containsKey(complement)) {\n return new int[]{numToIndex.get(complement), i};\n }\n numToIndex.put(nums[i], i);\n }\n throw new IllegalArgumentException("No solution found");\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n std::vector<int> twoSum(std::vector<int>& nums, int target) {\n std::unordered_map<int, int> numToIndex;\n for (int i = 0; i < nums.size(); i++) {\n int complement = target - nums[i];\n if (numToIndex.find(complement) != numToIndex.end()) {\n return {numToIndex[complement], i};\n }\n numToIndex[nums[i]] = i;\n }\n throw std::invalid_argument("No solution found");\n }\n};\n\n```\n\n | 34 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Two sums || 3 easy methods in Python | two-sum | 0 | 1 | # Intuition\nMethod 1: A brute-force solution to find two numbers in the nums list that add up to the target value.\n\nMethod 2: By list concept\n\nMethod 3: By Dictionary (more efficient solution)\n# Approach\nMethod 1: \nThe code uses nested loops to iterate over each pair of numbers in the nums list. The outer loop runs from 0 to len(nums)-1, and the inner loop runs from i+1 to len(nums)-1, where i is the current index of the outer loop. Within the nested loops, constant time operations are performed, such as checking if the sum of two numbers equals the target, appending indices to the a list, and using break and continue statements.\nTherefore, the overall time complexity of the code is O(n^2) due to the nested loops.\n\nMethod 2: \nThe code uses one loop to iterate over the number and subtract from target and if that subtracted number is present in list then return the index of both number. \n(here if condition of a==i means that possibly the target is 10 and present number in list might be [5,5] but it will return the same index so we need to skip)\n\nMethod 3: \nThe dictionary will help us to find the complement of each number more efficiently. In Method 2, Change the loop variable from i to num using the enumerate() function. This allows us to directly access the numbers from the nums list instead of using indexing.\nReplaced the variable p with complement to improve code readability.\nReplaced if p in nums with if complement in num_dict. This change allows us to check if the complement exists in the num_dict dictionary, which provides a more efficient lookup compared to the in operator on a list.\nModified the return statement to return [num_dict[complement], i] instead of i, a. This returns the indices of the two numbers that add up to the target, as required.\n\n\n# Complexity\n- Time complexity:\n\nMethod 1: \nO(n^2) due to nested loops\n\nMethod 2: \nO(n^2) because the the code uses a single loop that iterates over each element in the nums list which takes O(n) and index() method is called within the loop which takes O(n) time in the worst case to call the index of element.\n\nMethod 3: \n**O(n)** The use of the dictionary (num_dict) allows for efficient lookup of complements in constant time, improving the overall time complexity to O(n) compared to the previous methods with a time complexity of O(n^2) when using the brute force and index() method.\n\n\n- Space complexity:\nthe space complexity of the code is O(1) in all 3 methods.\n\n$$KINDLY$$ $$UPVOTE$$\n# Code\n\nMethod 1: \n```\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n a=[]\n for i in range(len(nums)):\n for j in range(i+1,len(nums)):\n if (nums[i]+nums[j]==target):\n a.append(i)\n a.append(j)\n break \n return a\n```\nMethod 2:\n```\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n a=0\n for i in range(len(nums)):\n p = target-nums[i]\n if p in nums:\n a=nums.index(p)\n if a==i:\n continue\n break\n return i,a\n```\nMethod 3:\n```\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n num_dict = {}\n for i, num in enumerate(nums):\n complement = target - num\n if complement in num_dict:\n return [num_dict[complement], i]\n num_dict[num] = i\n return []\n``` | 70 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
3 Best Solutions explained | two-sum | 1 | 1 | https://youtu.be/--qiegimDZM | 114 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Easy Python Solution With Explanation 🔥🔥 | two-sum | 0 | 1 | # Approach\nThis code defines a Python class called `Solution` with a method named `twoSum`. The purpose of this method is to find two numbers in a list (`nums`) that add up to a specific target number (`target`). Here\'s a simple explanation of how it works:\n\n1. Create an empty dictionary called `numsList` to store numbers from the list `nums` and their corresponding indices.\n \n2. Loop through each element (`n`) in the `nums` list along with its index (`i`).\n\n3. Calculate the difference (`diff`) between the `target` and the current number `n`. This difference represents the value we need to find in the list in order to reach the target.\n\n4. Check if the `diff` is already in the `numsList` dictionary. If it is, it means we have found a pair of numbers whose sum equals the target. In this case, return a list containing the indices of those two numbers: `[numsList[diff], i]`. This pair of indices will identify the two numbers in the original list that add up to the target.\n\n5. If the `diff` is not in the `numsList` dictionary, it means we haven\'t seen this number before. So, we add the current number `n` to the `numsList` dictionary, with its index `i` as the associated value. This allows us to look up this number later if we encounter its complement in the list.\n\n6. Repeat steps 3 to 5 for each number in the `nums` list until a pair of numbers that adds up to the `target` is found, at which point the function returns the indices of those numbers.\n\nIn summary, this code efficiently finds a pair of numbers in the `nums` list that add up to the given `target`, using a dictionary to keep track of the numbers seen so far and their indices.\n\n# Code\n```\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n numsList = {}\n for i,n in enumerate(nums):\n diff = target-n\n if diff in numsList:\n return [numsList[diff], i]\n else:\n numsList[n] = i\n```\n\n**Please upvote if you like the solution.\nHappy Coding! \uD83D\uDE0A** | 27 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
(VIDEO) Step-by-Step Visualization of O(n) Solution | two-sum | 0 | 1 | https://youtu.be/luicuNOBTAI\n\nInstead of checking every single combination of pairs, the key realization is that for each number in the array, there is only **one** number that can be added to it to reach the target.\n\nWe combine this with a hash table, which can look up values in constant time, to keep track of array elements and its indices as we traverse it. For each array element **x**, we calculate **target - x** and check if we\'ve encountered it in the array before.\n\nIn the worst case, the array will only have to be traversed once, resulting in an O(n) solution.\n\n# Code\n```\nclass Solution(object):\n def twoSum(self, nums, target):\n seen = {}\n for i in range(len(nums)):\n diff = target - nums[i]\n if diff in seen:\n return [seen[diff], i]\n else:\n seen[nums[i]] = i\n``` | 91 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
simple answer with for loop | two-sum | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nCreate an empty dictionary called num_dict to store numbers and their indices.\nIterate through the nums array using a for loop, keeping track of the current index and the current number.\nCalculate the complement, which is target - num, where num is the current number in the iteration.\nCheck if the complement is already in the num_dict dictionary. If it is, return the indices of the two numbers that add up to the target.\nIf the complement is not in the dictionary, add the current number and its index to the num_dict dictionary for future reference.\nIf no solution is found after iterating through the entire nums array, return an empty list to indicate that there is no valid pair of numbers that add up to the target.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution(object):\n def twoSum(self, nums, target):\n """\n :type nums: List[int]\n :type target: int\n :rtype: List[int]\n """\n num_dict = {} # Use a dictionary to store the numbers and their indices\n\n for i, num in enumerate(nums):\n complement = target - num\n # Check if the complement is in the dictionary\n if complement in num_dict:\n return [num_dict[complement], i]\n # Store the current number and its index in the dictionary\n num_dict[num] = i\n\n # If no solution is found, return an empty list\n return []\n``` | 2 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
Two Sum: faster than hashmap in worst case. uses sort | two-sum | 0 | 1 | # Better than Hashmap in worst case\n\nI\'ve seen a lot of solutions that iterate over the list and do hashmap lookup. These solutions often say that they are "worst case $$O(n)$$" time complexity. However, this is false because worst case hashmap lookup is $$O(n)$$, so those solutions are actually worst case $$O(n^2)$$. \n\nThose hashmap solutions have a place, since expected lookup complexity is $$O(1)$$, and thus the expected overall time complexity is $$O(n)$$. But, it\'s worth looking at what\'s the best possible solution for true worst case time complexity. Here\'s a solution that beats those solutions in the worst case.\n\nMy solution uses list sort, which has TC: $$O(nlog(n))$$, to solve this problem and thus has a better worst-case time complexity than using hashmaps.\n\n# Complexity\n- Time complexity (Expected and Worst Case): $$O(nlog(n))$$\n- Space complexity: $$O(n)$$\n\n# Overview\n\n1. Sort $$nums$$, the input list, while preserving original indices\n2. use a two-pointer technique to iterate from left and right simulatenously\n3. compare values at left index and right index, and move them accordingly\n4. when the values sum to target, return the original indices\n\n# Code\n```\nclass Solution:\n def twoSum(self, nums: List[int], target: int) -> List[int]:\n # TC O(nlog(n)), SC: O(n)\n\n # modify nums such that every element is a tuple (originalIndex, value)\n for index, value in enumerate(nums):\n nums[index] = (value, index)\n \n # sort nums by value\n nums.sort()\n\n # use a two-pointer technique to search from left and right.\n leftI = 0\n rightI = len(nums) - 1\n \n # this solution is guaranteed to converge. once it does, return the two originalIndex\'s of those values\n while (True):\n # get value on left and value on right. \n leftV, leftOriginalI = nums[leftI]\n rightV, rightOriginalI = nums[rightI]\n\n # compare to target\n if leftV + rightV == target:\n return (leftOriginalI, rightOriginalI)\n elif leftV + rightV > target:\n # if it\'s too large, move right pointer left\n rightI -= 1\n else:\n # if it\'s too small, move left pointer right\n leftI += 1\n\n \n \n\n \n\n``` | 0 | Given an array of integers `nums` and an integer `target`, return _indices of the two numbers such that they add up to `target`_.
You may assume that each input would have **_exactly_ one solution**, and you may not use the _same_ element twice.
You can return the answer in any order.
**Example 1:**
**Input:** nums = \[2,7,11,15\], target = 9
**Output:** \[0,1\]
**Explanation:** Because nums\[0\] + nums\[1\] == 9, we return \[0, 1\].
**Example 2:**
**Input:** nums = \[3,2,4\], target = 6
**Output:** \[1,2\]
**Example 3:**
**Input:** nums = \[3,3\], target = 6
**Output:** \[0,1\]
**Constraints:**
* `2 <= nums.length <= 104`
* `-109 <= nums[i] <= 109`
* `-109 <= target <= 109`
* **Only one valid answer exists.**
**Follow-up:** Can you come up with an algorithm that is less than `O(n2)` time complexity? | A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster? The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search? |
✅Beats 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | add-two-numbers | 1 | 1 | # Intuition:\nThe Intuition is to iterate through two linked lists representing non-negative integers in reverse order, starting from the least significant digit. It performs digit-wise addition along with a carry value and constructs a new linked list to represent the sum. The process continues until both input lists and the carry value are exhausted. The resulting linked list represents the sum of the input numbers in the correct order.\n\n# Explanation: \n1. Create a placeholder node called `dummyHead` with a value of 0. This node will hold the resulting linked list.\n2. Initialize a pointer called `tail` and set it to `dummyHead`. This pointer will keep track of the last node in the result list.\n3. Initialize a variable called `carry` to 0. This variable will store the carry value during addition.\n4. Start a loop that continues until there are no more digits in both input lists (`l1` and `l2`) and there is no remaining carry value.\n5. Inside the loop:\n - Check if there is a digit in the current node of `l1`. If it exists, assign its value to a variable called `digit1`. Otherwise, set `digit1` to 0.\n - Check if there is a digit in the current node of `l2`. If it exists, assign its value to a variable called `digit2`. Otherwise, set `digit2` to 0.\n - Add the current digits from `l1` and `l2`, along with the carry value from the previous iteration, and store the sum in a variable called `sum`.\n - Calculate the unit digit of `sum` by taking the modulus (`%`) of `sum` by 10. This digit will be placed in a new node for the result.\n - Update the `carry` variable by dividing `sum` by 10 and taking the integer division (`/`) part. This gives us the carry value for the next iteration.\n - Create a new node with the calculated digit as its value.\n - Attach the new node to the `tail` node of the result list.\n - Move the `tail` pointer to the newly added node.\n - Move to the next nodes in both `l1` and `l2`, if they exist. If either list is exhausted, set the corresponding pointer to `nullptr`.\n6. After the loop, obtain the actual result list by skipping the `dummyHead` node.\n7. Delete the `dummyHead` node.\n8. Return the resulting list.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {\n ListNode* dummyHead = new ListNode(0);\n ListNode* tail = dummyHead;\n int carry = 0;\n\n while (l1 != nullptr || l2 != nullptr || carry != 0) {\n int digit1 = (l1 != nullptr) ? l1->val : 0;\n int digit2 = (l2 != nullptr) ? l2->val : 0;\n\n int sum = digit1 + digit2 + carry;\n int digit = sum % 10;\n carry = sum / 10;\n\n ListNode* newNode = new ListNode(digit);\n tail->next = newNode;\n tail = tail->next;\n\n l1 = (l1 != nullptr) ? l1->next : nullptr;\n l2 = (l2 != nullptr) ? l2->next : nullptr;\n }\n\n ListNode* result = dummyHead->next;\n delete dummyHead;\n return result;\n }\n};\n```\n```Java []\nclass Solution {\n public ListNode addTwoNumbers(ListNode l1, ListNode l2) {\n ListNode dummyHead = new ListNode(0);\n ListNode tail = dummyHead;\n int carry = 0;\n\n while (l1 != null || l2 != null || carry != 0) {\n int digit1 = (l1 != null) ? l1.val : 0;\n int digit2 = (l2 != null) ? l2.val : 0;\n\n int sum = digit1 + digit2 + carry;\n int digit = sum % 10;\n carry = sum / 10;\n\n ListNode newNode = new ListNode(digit);\n tail.next = newNode;\n tail = tail.next;\n\n l1 = (l1 != null) ? l1.next : null;\n l2 = (l2 != null) ? l2.next : null;\n }\n\n ListNode result = dummyHead.next;\n dummyHead.next = null;\n return result;\n }\n}\n```\n```Python3 []\nclass Solution:\n def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:\n dummyHead = ListNode(0)\n tail = dummyHead\n carry = 0\n\n while l1 is not None or l2 is not None or carry != 0:\n digit1 = l1.val if l1 is not None else 0\n digit2 = l2.val if l2 is not None else 0\n\n sum = digit1 + digit2 + carry\n digit = sum % 10\n carry = sum // 10\n\n newNode = ListNode(digit)\n tail.next = newNode\n tail = tail.next\n\n l1 = l1.next if l1 is not None else None\n l2 = l2.next if l2 is not None else None\n\n result = dummyHead.next\n dummyHead.next = None\n return result\n```\n\n\n\n**If you are a beginner solve these problems which makes concepts clear for future coding:**\n1. [Two Sum](https://leetcode.com/problems/two-sum/solutions/3619262/3-method-s-c-java-python-beginner-friendly/)\n2. [Roman to Integer](https://leetcode.com/problems/roman-to-integer/solutions/3651672/best-method-c-java-python-beginner-friendly/)\n3. [Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/3651712/2-method-s-c-java-python-beginner-friendly/)\n4. [Maximum Subarray](https://leetcode.com/problems/maximum-subarray/solutions/3666304/beats-100-c-java-python-beginner-friendly/)\n5. [Remove Element](https://leetcode.com/problems/remove-element/solutions/3670940/best-100-c-java-python-beginner-friendly/)\n6. [Contains Duplicate](https://leetcode.com/problems/contains-duplicate/solutions/3672475/4-method-s-c-java-python-beginner-friendly/)\n7. [Add Two Numbers](https://leetcode.com/problems/add-two-numbers/solutions/3675747/beats-100-c-java-python-beginner-friendly/)\n8. [Majority Element](https://leetcode.com/problems/majority-element/solutions/3676530/3-methods-beats-100-c-java-python-beginner-friendly/)\n9. [Remove Duplicates from Sorted Array](https://leetcode.com/problems/remove-duplicates-from-sorted-array/solutions/3676877/best-method-100-c-java-python-beginner-friendly/)\n10. **Practice them in a row for better understanding and please Upvote the post for more questions.**\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.** | 921 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
[VIDEO] Step-by-Step Visualization and Explanation | add-two-numbers | 0 | 1 | ERROR: type should be string, got "https://www.youtube.com/watch?v=Fs5xgNNoP5c\\n\\nFirst we create a new ListNode, `head`, which will hold our answer. We then traverse the two lists, and at every node, we add the values together, create a new node with the sum, and link it to `head`. However, the problem is complicated by the need to keep track of <i>carries</i>. Here\\'s how we deal with it. After adding two digits together:\\n\\n- The <i>non-carry</i> part is obtained by doing `total % 10`. By taking the remainder of a number after dividing by 10, we only get what\\'s left in the ones place. For example, if the total is 15, then 15 % 10 = 5, so we create a new ListNode with value 5 and link it to `head`\\n- The <i>carry</i> is obtained by doing `total // 10` (floor division by 10). By dividing by 10 and rounding down, we get the carry value. So 15 // 10 = 1 (1.5 rounded down is 1) so that corresponds to a carry of 1.\\n\\nWe then keep repeating this until all lists have reached the end AND there are no more carry values. At the end, `head.next`holds the very first node of our answer, so we return `head.next`.\\n\\n# Code\\n```\\n# Definition for singly-linked list.\\n# class ListNode(object):\\n# def __init__(self, val=0, next=None):\\n# self.val = val\\n# self.next = next\\nclass Solution(object):\\n def addTwoNumbers(self, l1, l2):\\n head = ListNode()\\n current = head\\n carry = 0\\n while (l1 != None or l2 != None or carry != 0):\\n l1_value = l1.val if l1 else 0\\n l2_value = l2.val if l2 else 0\\n total = l1_value + l2_value + carry\\n current.next = ListNode(total % 10)\\n carry = total // 10\\n # Move list pointers forward\\n l1 = l1.next if l1 else None\\n l2 = l2.next if l2 else None\\n current = current.next\\n return head.next\\n```" | 6 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
(PYTHON) In-Place, O(N) 90%+ Speed, 60%+ Space. Easy to Understand. | add-two-numbers | 0 | 1 | # Intuition\nFor each pair of Nodes in l1 and l2, find their "raw" sum along with the carryover. Use modulo to get the digit and floor division to get the carry over. Then connect the remainder of l2 to the end of l1 (if it is longer). Continue the original process, ommiting the l2.val sum. \n\n# Complexity\n- Time complexity:\nShould be O(N), as we traverse both lists exactly once using only O(1) operations for each iteration.\n\n- Space complexity:\nWe create at most 1 new node, giving us O(N) space complexity.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n carry_over = 0\n head = l1\n l1_prev = None\n while l1 and l2:\n raw_val = carry_over + l1.val + l2.val\n # What digit goes in node\n l1.val = raw_val % 10\n # What carries over\n carry_over = raw_val // 10\n # Increment prev\n l1_prev = l1\n # Incerement pointers\n l1 = l1.next\n l2 = l2.next\n\n # If l1 ran out BEFORE l2\n if l2:\n l1_prev.next = l2\n l1 = l2\n\n # We now may have more l1, then continue carryover process\n while l1:\n raw_val = carry_over + l1.val\n # What digit goes in node\n l1.val = raw_val % 10\n # What carries over\n carry_over = raw_val // 10\n # Incerement pointers\n l1_prev = l1\n l1 = l1.next\n if carry_over > 0:\n l1_prev.next = ListNode(val = carry_over)\n return head\n\n\n\n\n``` | 3 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
Python Code For Beginners Full Recursion | add-two-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def helper(self,l1,l2,carry):\n if not l1 and not l2:\n if carry > 0:\n return ListNode(carry)\n return None\n \n if l1 and not l2:\n val = (l1.val+carry)\n carry = val//10\n head = ListNode(val%10)\n head.next = self.helper(l1.next,l2,carry)\n return head\n\n if l2 and not l1:\n val = (l2.val+carry)\n carry = val//10\n head = ListNode(val%10)\n head.next = self.helper(l1,l2.next,carry)\n return head\n \n val = (l1.val+l2.val+carry)\n carry = val//10\n head = ListNode(val%10)\n head.next = self.helper(l1.next,l2.next,carry)\n return head\n\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n return self.helper(l1,l2,0)\n``` | 1 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
Python 99.90 % beats || Easy Solution | add-two-numbers | 0 | 1 | # Your upvote is my motivation!\n\n\n# Code\n```\n# Definition for singly-linked list.\n# Definition for singly-linked list.\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n dummyHead = ListNode(0)\n curr = dummyHead\n carry = 0\n while l1 != None or l2 != None or carry != 0:\n l1Val = l1.val if l1 else 0\n l2Val = l2.val if l2 else 0\n columnSum = l1Val + l2Val + carry\n carry = columnSum // 10\n newNode = ListNode(columnSum % 10)\n curr.next = newNode\n curr = newNode\n l1 = l1.next if l1 else None\n l2 = l2.next if l2 else None\n return dummyHead.next\n\n\n<!-- ========================================================= -->\n# Long Approach to understand\n<!-- Same Approach but diff way -- 99.9% beats in Memory -->\n\n newhead = ListNode(-1)\n temphead = newhead\n c = 0\n\n while l1 and l2:\n cur_digit = l1.val + l2.val + c # 25\n\n if cur_digit >= 10:\n c = cur_digit // 10 #2\n cur_digit = cur_digit % 10 #5\n else:\n c = 0\n \n new_node = ListNode(cur_digit)\n temphead.next = new_node\n temphead = new_node\n \n l1 = l1.next\n l2 = l2.next\n \n while l1:\n cur_digit = l1.val + c\n if cur_digit >= 10:\n c = cur_digit // 10 #2\n cur_digit = cur_digit % 10 #5\n else:\n c = 0\n new_node = ListNode(cur_digit)\n temphead.next = new_node\n temphead = new_node\n l1 = l1.next\n \n while l2:\n cur_digit = l2.val + c\n if cur_digit >= 10:\n c = cur_digit // 10 #2\n cur_digit = cur_digit % 10 #5\n else:\n c = 0\n new_node = ListNode(cur_digit)\n temphead.next = new_node\n temphead = new_node\n l2 = l2.next\n \n if c == 0:\n return newhead.next\n else:\n new_node = ListNode(c)\n temphead.next = new_node\n return newhead.next\n\n``` | 18 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
2. Add Two Numbers | add-two-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n # Creating a dummy node for reference\n dummynode= ListNode(0)\n current=dummynode\n carry=0\n\n while l1!= None or l2 != None or carry !=0:\n # Checking if a node exists in the list\n l1value = l1.val if l1 else 0\n l2value = l2.val if l2 else 0\n sum= l1value+l2value+carry\n carry = sum //10 # Adding quotient value to carry\n current.next= ListNode(sum%10) # Adding remainder value to the node\n # Updating list node pointers\n current= current.next\n l1=l1.next if l1 else None\n l2=l2.next if l2 else None\n\n return dummynode.next \n\n\n\n\n\n \n\n \n``` | 2 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
✅Mastering Adding Two Number 💡 Beginner's Guide | add-two-numbers | 1 | 1 | # Adding Two Numbers - LeetCode Problem #2\n---\n---\n\n## \uD83D\uDCA1Approach 1: Recursive Approach\n---\n\n### \u2728Explanation\nIn this approach, we recursively traverse both linked lists `l1` and `l2`, adding their corresponding nodes and handling carry if necessary. We create a new linked list `p` to store the sum.\n\n### \uD83D\uDCDDDry Run\nLet\'s dry run this approach with an example:\n- `l1` = 2 -> 4 -> 3\n- `l2` = 5 -> 6 -> 4\nAdding the numbers:\n- First, we add 2 and 5, resulting in 7.\n- Then, we add 4 and 6, resulting in 10 (with a carry of 1).\n- Finally, we add 3 and 4 with the carry, resulting in 8 (with no carry).\n\nThe resulting linked list `p` will be 7 -> 0 -> 8.\n\n### \uD83D\uDD0DEdge Cases\nThis approach handles cases where the linked lists have different lengths or carry values.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: O(max(N, M)), where N and M are the lengths of `l1` and `l2`.\n- Space Complexity: O(max(N, M)), as the result linked list can be at most one element longer than the longer of the two input lists.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes\n\n```cpp []\nclass Solution {\npublic:\n ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {\n if (!l1 && !l2) return NULL;\n else if (!l1) return l2;\n else if (!l2) return l1;\n\n int a = l1->val + l2->val;\n ListNode* p = new ListNode(a % 10);\n p->next = addTwoNumbers(l1->next, l2->next);\n if (a >= 10) p->next = addTwoNumbers(p->next, new ListNode(1));\n return p;\n }\n};\n```\n\n```java []\npublic class Solution {\n public ListNode addTwoNumbers(ListNode l1, ListNode l2) {\n if (l1 == null && l2 == null) return null;\n else if (l1 == null) return l2;\n else if (l2 == null) return l1;\n\n int a = l1.val + l2.val;\n ListNode p = new ListNode(a % 10);\n p.next = addTwoNumbers(l1.next, l2.next);\n if (a >= 10) p.next = addTwoNumbers(p.next, new ListNode(1));\n return p;\n }\n}\n```\n\n```python []\nclass Solution:\n def addTwoNumbers(self, l1, l2):\n if not l1 and not l2:\n return None\n elif not l1:\n return l2\n elif not l2:\n return l1\n\n a = l1.val + l2.val\n p = ListNode(a % 10)\n p.next = self.addTwoNumbers(l1.next, l2.next)\n if a >= 10:\n p.next = self.addTwoNumbers(p.next, ListNode(1))\n return p\n```\n\n```csharp []\npublic class Solution {\n public ListNode AddTwoNumbers(ListNode l1, ListNode l2) {\n if (l1 == null && l2 == null) return null;\n else if (l1 == null) return l2;\n else if (l2 == null) return l1;\n\n int a = l1.val + l2.val;\n ListNode p = new ListNode(a % 10);\n p.next = AddTwoNumbers(l1.next, l2.next);\n if (a >= 10) p.next = AddTwoNumbers(p.next, new ListNode(1));\n return p;\n }\n}\n```\n\n```javascript []\nvar addTwoNumbers = function(l1, l2) {\n if (!l1 && !l2) return null;\n else if (!l1) return l2;\n else if (!l2) return l1;\n\n var a = l1.val + l2.val;\n var p = new ListNode(a % 10);\n p.next = addTwoNumbers(l1.next, l2.next);\n if (a >= 10) p.next = addTwoNumbers(p.next, new ListNode(1));\n return p;\n};\n```\n\n---\n## \uD83D\uDCCA Analysis\n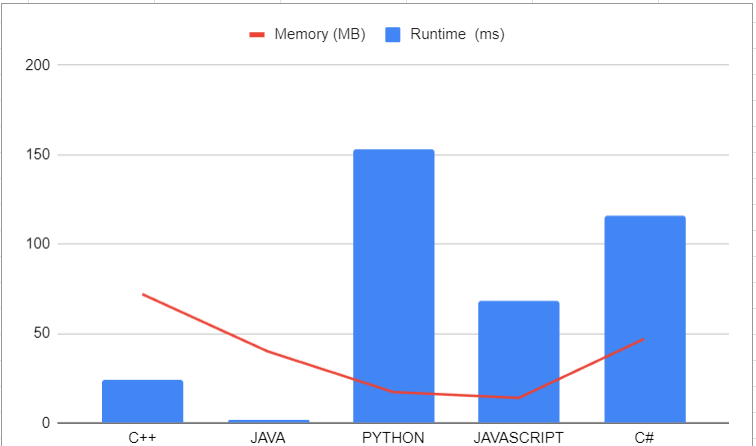\n\n\n---\n# \uD83D\uDCA1Approach 2: Using Dummy Node and Iteration\n---\n## \u2728Explanation\n\nThe problem statement requires us to add two numbers represented by two linked lists, where each node contains a single digit. We need to return the sum as a new linked list.\n\nThe third approach involves using a dummy node to simplify the code. It also uses an iterative process to construct the result linked list.\n\nHere are the steps for this approach:\n\n1. Create a dummy node `dummy_head` to hold the result. Initialize it with a value of 0.\n\n2. Initialize two pointers, `p` and `q`, both pointing to `dummy_head`. These pointers will be used to construct the result linked list.\n\n3. Initialize a carry variable `carry` to 0. This will store the carry generated during addition.\n\n4. Loop through the input linked lists `l1` and `l2` until both are empty.\n\n5. Within the loop, add the values of the current nodes in `l1` and `l2`, along with the carry. Calculate the sum as `(l1->val + l2->val + carry)`. Also, update the carry as `(l1->val + l2->val + carry) / 10`.\n\n6. Create a new node with the value `(l1->val + l2->val + carry) % 10`, and set this value as the next node of `p`.\n\n7. Update `p` to point to the newly created node.\n\n8. Move the pointers `l1` and `l2` to their next nodes.\n\n9. After the loop, check if there is any remaining carry. If so, create a new node with the carry and attach it to the result.\n\n10. Finally, return `dummy_head->next`, which is the actual result.\n\n## \uD83D\uDCDDDry Run\n\nLet\'s dry run this approach with an example:\n\n- Input:\n - `l1`: 2 -> 4 -> 3\n - `l2`: 5 -> 6 -> 4\n\n- Initialize `dummy_head` with value 0.\n\n- Initialize pointers:\n - `p` is at `dummy_head`\n - `q` is at `dummy_head`\n - `l1` points to 2\n - `l2` points to 5\n\n- Begin the loop:\n - Calculate the sum with carry: `(2 + 5) % 10 = 7`.\n - Set `p->next` to a new node with the value 7.\n - Update `carry` to `(2 + 5) / 10 = 0`.\n - Move `p` to the new node (7).\n - Move `q` to the new node (7).\n - Move `l1` to 4 and `l2` to 6.\n\n- Continue the loop:\n - Calculate the sum with carry: `(4 + 6) % 10 = 0`.\n - Set `p->next` to a new node with the value 0.\n - Update `carry` to `(4 + 6) / 10 = 1`.\n - Move `p` to the new node (0).\n - Move `q` to the new node (0).\n - Move `l1` to 3 and `l2` to 4.\n\n- Continue the loop:\n - Calculate the sum with carry: `(3 + 4 + 1) % 10 = 8`.\n - Set `p->next` to a new node with the value 8.\n - Update `carry` to `(3 + 4 + 1) / 10 = 0`.\n - Move `p` to the new node (8).\n - Move `q` to the new node (8).\n - Move `l1` to null and `l2` to null.\n\n- Loop ends, but there\'s no remaining carry.\n\n- Return `dummy_head->next`, which is the actual result: 7 -> 0 -> 8.\n\n## \uD83D\uDD0DEdge Cases\n\nThis approach efficiently handles cases where the linked lists have different lengths or carry values. It ensures that the result is correct and accurately represents the sum of the numbers.\n\n## \uD83D\uDD78\uFE0FComplexity Analysis\n\n- Time Complexity: O(max(N, M)), where N and M are the lengths of `l1` and `l2`. The algorithm iterates through both linked lists once.\n- Space Complexity: O(max(N, M)), as we only use a few extra variables, such as `dummy_head`, `p`, `q`, and `carry`, to construct the result linked list.\n\n## \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes\n\n\n```cpp []\nclass Solution {\npublic:\nListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {\n ListNode* dummy_head = new ListNode(0);\n ListNode* p = dummy_head;\n ListNode* q = dummy_head;\n int carry = 0;\n \n while (l1 || l2) {\n int x = l1 ? l1->val : 0;\n int y = l2 ? l2->val : 0;\n \n int _sum = x + y + carry;\n carry = _sum / 10;\n \n p->next = new ListNode(_sum % 10);\n p = p->next;\n \n if (l1) l1 = l1->next;\n if (l2) l2 = l2->next;\n }\n \n if (carry > 0) {\n p->next = new ListNode(carry);\n }\n \n ListNode* result = dummy_head->next;\n delete dummy_head;\n \n return result;\n}\n};\n```\n\n```python []\nclass Solution:\n def addTwoNumbers(self, l1, l2):\n dummy_head = ListNode(0)\n p = dummy_head\n q = dummy_head\n carry = 0\n\n while l1 or l2:\n x = l1.val if l1 else 0\n y = l2.val if l2 else 0\n\n _sum = x + y + carry\n carry = _sum // 10\n\n p.next = ListNode(_sum % 10)\n p = p.next\n\n if l1:\n l1 = l1.next\n if l2:\n l2 = l2.next\n\n if carry > 0:\n p.next = ListNode(carry)\n\n result = dummy_head.next\n return result\n\n```\n\n```java []\npublic class Solution {\n public ListNode addTwoNumbers(ListNode l1, ListNode l2) {\n ListNode dummy_head = new ListNode(0);\n ListNode p = dummy_head;\n ListNode q = dummy_head;\n int carry = 0;\n\n while (l1 != null || l2 != null) {\n int x = (l1 != null) ? l1.val : 0;\n int y = (l2 != null) ? l2.val : 0;\n\n int _sum = x + y + carry;\n carry = _sum / 10;\n\n p.next = new ListNode(_sum % 10);\n p = p.next;\n\n if (l1 != null) l1 = l1.next;\n if (l2 != null) l2 = l2.next;\n }\n\n if (carry > 0) {\n p.next = new ListNode(carry);\n }\n\n ListNode result = dummy_head.next;\n return result;\n }\n}\n```\n\n```csharp []\npublic class Solution {\n public ListNode AddTwoNumbers(ListNode l1, ListNode l2) {\n ListNode dummy_head = new ListNode(0);\n ListNode p = dummy_head;\n ListNode q = dummy_head;\n int carry = 0;\n\n while (l1 != null || l2 != null) {\n int x = (l1 != null) ? l1.val : 0;\n int y = (l2 != null) ? l2.val : 0;\n\n int _sum = x + y + carry;\n carry = _sum / 10;\n\n p.next = new ListNode(_sum % 10);\n p = p.next;\n\n if (l1 != null) l1 = l1.next;\n if (l2 != null) l2 = l2.next;\n }\n\n if (carry > 0) {\n p.next = new ListNode(carry);\n }\n\n ListNode result = dummy_head.next;\n return result;\n }\n}\n```\n\n```javascript []\n\nvar addTwoNumbers = function (l1, l2) {\n let dummy_head = new ListNode(0);\n let p = dummy_head;\n let q = dummy_head;\n let carry = 0;\n\n while (l1 || l2) {\n const x = l1 ? l1.val : 0;\n const y = l2 ? l2.val : 0;\n\n const _sum = x + y + carry;\n carry = Math.floor(_sum / 10);\n\n p.next = new ListNode(_sum % 10);\n p = p.next;\n\n if (l1) l1 = l1.next;\n if (l2) l2 = l2.next;\n }\n\n if (carry > 0) {\n p.next = new ListNode(carry);\n }\n\n const result = dummy_head.next;\n return result;\n}\n\n```\n\n```ruby []\n\ndef add_two_numbers(l1, l2)\n dummy_head = ListNode.new(0)\n p = dummy_head\n q = dummy_head\n carry = 0\n\n while l1 || l2\n x = l1 ? l1.val : 0\n y = l2 ? l2.val : 0\n\n _sum = x + y + carry\n carry = _sum / 10\n\n p.next = ListNode.new(_sum % 10)\n p = p.next\n\n if l1\n l1 = l1.next\n end\n\n if l2\n l2 = l2.next\n end\n end\n\n if carry > 0\n p.next = ListNode.new(carry)\n end\n\n result = dummy_head.next\n return result\nend\n```\n---\n## \uD83D\uDCCA Analysis\n| Language | Runtime | Memory |\n|----------|---------|--------|\n| C++ | 24 ms | 71.5 MB |\n| Java | 2 ms | 39.8 MB |\n| Python | 68 ms | 14.3 MB |\n| C# | 116 ms | 26.3 MB |\n| JavaScript | 108 ms | 46.7 MB |\n\n---\n\n---\n\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n\n | 3 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
Easy way of suming for pyhton | add-two-numbers | 0 | 1 | # Intuition\n<!-- Transfer to int and then back to linked list -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n num1 = 0 \n num2 = 0\n count= 1\n while(l1):\n num1+=l1.val*count\n count = count*10\n l1=l1.next \n count = 1\n while(l2):\n num2+=l2.val*count\n count = count*10\n l2=l2.next \n result = num1+ num2\n finalh= ListNode(-1)\n helper = finalh\n if (result==0):\n return ListNode(0)\n while(result!=0):\n helper.next = ListNode(result%10)\n result = result//10\n helper = helper.next\n return finalh.next\n\n\n``` | 0 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
listNode, newNode | add-two-numbers | 0 | 1 | # Code\n```\nclass ListNode:\n def __init__(self, val=0, next=None):\n self.val = val\n self.next = next\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n dummy = ListNode(0)\n curr = dummy\n carry = 0\n while l1 != None or l2 != None or carry != 0:\n l1val = l1.val if l1 != None else 0\n l2val = l2.val if l2 != None else 0\n whole_sum = l1val + l2val + carry\n carry = whole_sum // 10\n newNode = ListNode(whole_sum % 10)\n curr.next = newNode \n curr = curr.next\n l1 = l1.next if l1 != None else l1\n l2 = l2.next if l2 != None else l2\n \n return dummy.next\n\n``` | 0 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
Easy | Solution | Python |Linked List | add-two-numbers | 0 | 1 | # Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:\n d = n = ListNode(0)\n num1 = num2 = ""\n while l1:\n num1 += str(l1.val)\n l1 = l1.next\n while l2:\n num2 += str(l2.val)\n l2 = l2.next\n res = str(int(num1[::-1]) + int(num2[::-1]))[::-1]\n for i in res:\n d.next = ListNode(i)\n d = d.next\n return n.next \n```\nDo upvote if you like the Solution :) | 59 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
100% Beats | Java | C++ | Python | Javascript | C# | PHP | add-two-numbers | 1 | 1 | \n### steps\n1. Initialize a dummy node and a current node to keep track of the result linked list.\n2. Initialize carry to 0.\n3. Traverse both input linked lists simultaneously.\n4. At each step, calculate the sum of the current nodes\' values along with the carry.\n5. Calculate the carry for the next iteration as sum / 10.\n6. Create a new node with the value sum % 10 and append it to the result list.\n7. Move to the next nodes in both input lists.\n8. Repeat steps 4-7 until you have processed all digits in both input lists.\n9. If there is still a carry left after the loop, create an additional node with the carry as its value and append it to the result list.\n10. Return the next node of the dummy node, which represents the head of the result linked list.\n\n\n``` java []\nclass Solution {\n public ListNode addTwoNumbers(ListNode l1, ListNode l2) {\n ListNode dummy = new ListNode(0); // Dummy node to simplify result list handling\n ListNode current = dummy; // Current node to build the result list\n int carry = 0; // Initialize carry to 0\n\n while (l1 != null || l2 != null) {\n int x = (l1 != null) ? l1.val : 0; // Get the current digit from l1 or set to 0 if null\n int y = (l2 != null) ? l2.val : 0; // Get the current digit from l2 or set to 0 if null\n\n int sum = x + y + carry; // Calculate the sum of digits and carry\n carry = sum / 10; // Calculate the carry for the next iteration\n\n // Create a new node with the value sum % 10 and append it to the result list\n current.next = new ListNode(sum % 10);\n current = current.next; // Move to the next node in the result list\n\n // Move to the next nodes in both input lists if they are not null\n if (l1 != null) l1 = l1.next;\n if (l2 != null) l2 = l2.next;\n }\n\n // If there is still a carry left after the loop, create an additional node for it\n if (carry > 0) {\n current.next = new ListNode(carry);\n }\n\n return dummy.next; // Return the next node of the dummy node, which is the head of the result list\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {\n ListNode* dummy_head = new ListNode(0); // Dummy head to simplify the code\n ListNode* current = dummy_head;\n int carry = 0;\n\n while (l1 || l2) {\n int x = (l1) ? l1->val : 0;\n int y = (l2) ? l2->val : 0;\n int sum = x + y + carry;\n\n carry = sum / 10;\n current->next = new ListNode(sum % 10);\n current = current->next;\n\n if (l1) l1 = l1->next;\n if (l2) l2 = l2->next;\n }\n\n if (carry > 0) {\n current->next = new ListNode(carry);\n }\n\n return dummy_head->next; // Return the actual result, not the dummy head.\n\n }\n};\n```\n``` Python []\n\ndef addTwoNumbers(l1, l2):\n dummy = ListNode()\n current = dummy\n p, q = l1, l2\n carry = 0\n \n while p or q:\n x = p.val if p else 0\n y = q.val if q else 0\n val = carry + x + y\n carry = val // 10\n current.next = ListNode(val % 10)\n current = current.next\n \n if p:\n p = p.next\n if q:\n q = q.next\n \n if carry > 0:\n current.next = ListNode(carry)\n \n return dummy.next\n\n```\n``` javascript []\nvar addTwoNumbers = function(l1, l2) {\n let dummyHead = new ListNode(0); // Create a dummy node to simplify the code.\n let current = dummyHead; // Initialize a current pointer to the dummy node.\n let carry = 0; // Initialize a variable to store the carry value.\n\n while (l1 || l2) {\n const x = l1 ? l1.val : 0;\n const y = l2 ? l2.val : 0;\n const sum = x + y + carry;\n\n carry = Math.floor(sum / 10); // Calculate the carry for the next iteration.\n current.next = new ListNode(sum % 10); // Create a new node with the current digit.\n\n current = current.next; // Move the current pointer to the next node.\n\n if (l1) l1 = l1.next;\n if (l2) l2 = l2.next;\n }\n\n // If there is a carry after processing all digits, add it as a new node.\n if (carry > 0) {\n current.next = new ListNode(carry);\n }\n\n return dummyHead.next; // Return the result, skipping the dummy node.\n}\n```\n\n``` C# []\npublic class Solution {\n public ListNode AddTwoNumbers(ListNode l1, ListNode l2) {\n ListNode dummyHead = new ListNode();\n ListNode current = dummyHead;\n int carry = 0;\n\n while (l1 != null || l2 != null)\n {\n int x = (l1 != null) ? l1.val : 0;\n int y = (l2 != null) ? l2.val : 0;\n\n int sum = x + y + carry;\n carry = sum / 10;\n\n current.next = new ListNode(sum % 10);\n current = current.next;\n\n if (l1 != null) l1 = l1.next;\n if (l2 != null) l2 = l2.next;\n }\n\n if (carry > 0)\n {\n current.next = new ListNode(carry);\n }\n\n return dummyHead.next; \n }\n}\n```\n\n``` PHP []\n\nfunction addTwoNumbers($l1, $l2) {\n $dummy = new ListNode(0);\n $current = $dummy;\n $carry = 0;\n \n while ($l1 !== null || $l2 !== null) {\n $x = ($l1 !== null) ? $l1->val : 0;\n $y = ($l2 !== null) ? $l2->val : 0;\n \n $sum = $x + $y + $carry;\n $carry = (int)($sum / 10);\n \n $current->next = new ListNode($sum % 10);\n $current = $current->next;\n \n if ($l1 !== null) $l1 = $l1->next;\n if ($l2 !== null) $l2 = $l2->next;\n }\n \n if ($carry > 0) {\n $current->next = new ListNode($carry);\n }\n \n return $dummy->next;\n}\n``` | 19 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
✅Python3 78ms memory efficient🔥🔥 | add-two-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Normal list traversal and adding numbers.**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- we used **yield** here because it\'s very memory efficient.\n- forward function used to get in-sequence value of linked list, we used yield because it\'s more memory efficient.\n- traverse linked list in given order, if one list is smaller than other than **pad 0 as num**.\n- add respective number with carry.\n- if computed is less or equal to 9 then carry is 0, **create link node** with $$value = val$$.\n- else $$carry = val // 10$$, and $$val = val - 10$$, create node for respective value.\n- at last if we have any carry left then create node with value carry else make last node\'s next as None(becaues this is end)\n- return root\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport itertools as it\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n def forward(curr = None):\n if curr:\n yield curr.val\n for i in forward(curr.next):\n yield i\n def add():\n root = ListNode(-1,None)\n ans = root\n straightL1 = forward(l1)\n straightL2 = forward(l2)\n carry = 0\n last = None\n for num1, num2 in it.zip_longest(straightL1, straightL2, fillvalue=0):\n val = carry+num1+num2\n if val <= 9:\n carry = 0\n ans.val = val\n ans.next = ListNode(0, None)\n last = ans\n ans = ans.next\n else:\n carry = val // 10\n val -= 10\n ans.val = val\n ans.next = ListNode(0, None)\n last = ans\n ans = ans.next\n last.next = None\n if carry:\n last.next = ListNode(carry, None)\n return root\n return add()\n```\n# Please like and comment below \uD83D\uDC4B\u2267\u25C9\u1D25\u25C9\u2266 | 3 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
Beginner | Simple | Python Solution 😁 | add-two-numbers | 0 | 1 | # *Intuition*\n<!-- Describe your first thoughts on how to solve this problem. -->\n- *We get numbers and add them.*\n# *Approach*\n<!-- Describe your approach to solving the problem. -->\n- *The first thing that comes to mind is that we must obtain the numbers from both lists so that we may utilise them for addition later.*\n- *Then we use that number to create a linked list (**reversed**).*\n- *and send its head node back.*\n# Complexity\n- *Time complexity: **O(N)***\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- *Space complexity: **O(N)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# *Code*\n### Python\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n def get_num(head):\n num = 0\n p = 0\n trav = head\n while trav:\n num += trav.val * (10 ** p)\n p += 1\n trav = trav.next\n return num\n\n\n def sum(h1, h2) -> ListNode:\n n1 = get_num(h1)\n n2 = get_num(h2)\n s = str(n1 + n2)\n\n head = ListNode(-1)\n trav = head\n for num in s[::-1]:\n trav.next = ListNode(int(num))\n trav = trav.next\n return head.next\n\n return sum(l1,l2)\n``` | 2 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
Easy step by step solution | add-two-numbers | 0 | 1 | \n# Approach\n1. Firstly, get all the elements from both LL\n2. Reverse those numbers\n3. Convert them from array to two numbers\n4. Convert the sum of those numbers to array of digits\n5. Create new LL from that array of digits\n\nHope you find it useful and if so, please upvote, cause it`s my first solution\n\n# Complexity\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) :\n curr = head = ListNode(0)\n nums1 = []\n nums2 = []\n number1 = 0\n number2 = 0\n while l1:\n nums1.append(l1.val)\n l1 = l1.next\n while l2:\n nums2.append(l2.val)\n l2 = l2.next\n nums1.reverse()\n nums2.reverse()\n for i in range(len(nums1)):\n if i == 0: number1 = nums1[i]\n else: number1 = number1 * 10 + nums1[i]\n for i in range(len(nums2)):\n if i == 0: number2 = nums2[i]\n else: number2 = number2 * 10 + nums2[i]\n sum_nums = [int(char) for char in str(number1 + number2)]\n sum_nums.reverse()\n for element in sum_nums:\n curr.next = ListNode(element)\n curr = curr.next\n curr.next = None\n return head.next\n``` | 2 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
Represented as linked lists | add-two-numbers | 0 | 1 | # Intuition\nwe need to perform addition similarly to how we add numbers manually, taking care of carrying values when the sum exceeds 9\n\n# Approach\n1. Initialize a dummy node and a pointer current to keep track of the current node in the result linked list.\n\n2. Start iterating through both input linked lists (l1 and l2) from the head while at least one of them has nodes.\n\n3. At each step, calculate the sum of the current nodes in l1 and l2, along with any carry from the previous step.\n\n4. Create a new node with the value as the sum modulo 10 and update the carry for the next step.\n\n5. Move the current pointer to the newly created node.\n\n6. If there are more nodes in l1 or l2, move to the next node in the respective list.\n\n7. After the loop, if there\'s a remaining carry, create a new node with that value.\n\n8. Return the result linked list starting from the second node (the first node is the dummy node).\n\n# Complexity\n- Time complexity:\n\nthe algorithm has a time complexity of O(max(N, M)), where N and M are the lengths of the input linked lists l1 and l2. We iterate through both lists once, so the time complexity is linear with respect to the length of the longer list\n\n- Space complexity:\n\nThe space complexity is O(max(N, M)), which is the space required for the output linked list. The additional space is used for the dummy node, the result linked list, and the carry value. It\'s linear with respect to the length of the longer list.\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\nclass Solution:\n def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:\n dummy = ListNode(0)\n current = dummy\n carry = 0\n\n while l1 or l2:\n x = l1.val if l1 else 0\n y = l2.val if l2 else 0\n _sum = x + y + carry\n carry = _sum // 10\n\n current.next = ListNode(_sum % 10)\n current = current.next\n\n if l1:\n l1 = l1.next\n if l2:\n l2 = l2.next\n\n if carry > 0:\n current.next = ListNode(carry)\n\n return dummy.next\n\n``` | 2 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
**Example 1:**
**Input:** l1 = \[2,4,3\], l2 = \[5,6,4\]
**Output:** \[7,0,8\]
**Explanation:** 342 + 465 = 807.
**Example 2:**
**Input:** l1 = \[0\], l2 = \[0\]
**Output:** \[0\]
**Example 3:**
**Input:** l1 = \[9,9,9,9,9,9,9\], l2 = \[9,9,9,9\]
**Output:** \[8,9,9,9,0,0,0,1\]
**Constraints:**
* The number of nodes in each linked list is in the range `[1, 100]`.
* `0 <= Node.val <= 9`
* It is guaranteed that the list represents a number that does not have leading zeros. | null |
✅3 Method's || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | longest-substring-without-repeating-characters | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the 3 solutions is to iteratively find the longest substring without repeating characters by maintaining a sliding window approach. We use two pointers (`left` and `right`) to represent the boundaries of the current substring. As we iterate through the string, we update the pointers and adjust the window to accommodate new unique characters and eliminate repeating characters.\n\n# Approach 1 - Set\n<!-- Describe your approach to solving the problem. -->\n\n1. We use a set (`charSet`) to keep track of unique characters in the current substring.\n2. We maintain two pointers, `left` and `right`, to represent the boundaries of the current substring.\n3. The `maxLength` variable keeps track of the length of the longest substring encountered so far.\n4. We iterate through the string using the `right` pointer.\n5. If the current character is not in the set (`charSet`), it means we have a new unique character.\n6. We insert the character into the set and update the `maxLength` if necessary.\n7. If the character is already present in the set, it indicates a repeating character within the current substring.\n8. In this case, we move the `left` pointer forward, removing characters from the set until the repeating character is no longer present.\n9. We insert the current character into the set and continue the iteration.\n10. Finally, we return the `maxLength` as the length of the longest substring without repeating characters.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int lengthOfLongestSubstring(string s) {\n int n = s.length();\n int maxLength = 0;\n unordered_set<char> charSet;\n int left = 0;\n \n for (int right = 0; right < n; right++) {\n if (charSet.count(s[right]) == 0) {\n charSet.insert(s[right]);\n maxLength = max(maxLength, right - left + 1);\n } else {\n while (charSet.count(s[right])) {\n charSet.erase(s[left]);\n left++;\n }\n charSet.insert(s[right]);\n }\n }\n \n return maxLength;\n }\n};\n```\n```Java []\nclass Solution {\n public int lengthOfLongestSubstring(String s) {\n int n = s.length();\n int maxLength = 0;\n Set<Character> charSet = new HashSet<>();\n int left = 0;\n \n for (int right = 0; right < n; right++) {\n if (!charSet.contains(s.charAt(right))) {\n charSet.add(s.charAt(right));\n maxLength = Math.max(maxLength, right - left + 1);\n } else {\n while (charSet.contains(s.charAt(right))) {\n charSet.remove(s.charAt(left));\n left++;\n }\n charSet.add(s.charAt(right));\n }\n }\n \n return maxLength;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n n = len(s)\n maxLength = 0\n charSet = set()\n left = 0\n \n for right in range(n):\n if s[right] not in charSet:\n charSet.add(s[right])\n maxLength = max(maxLength, right - left + 1)\n else:\n while s[right] in charSet:\n charSet.remove(s[left])\n left += 1\n charSet.add(s[right])\n \n return maxLength\n\n```\n\n# Approach 2 - Unordered Map\n1. We improve upon the first solution by using an unordered map (`charMap`) instead of a set.\n2. The map stores characters as keys and their indices as values.\n3. We still maintain the `left` and `right` pointers and the `maxLength` variable.\n4. We iterate through the string using the `right` pointer.\n5. If the current character is not in the map or its index is less than `left`, it means it is a new unique character.\n6 We update the `charMap` with the character\'s index and update the `maxLength` if necessary.\n7. If the character is repeating within the current substring, we move the `left` pointer to the next position after the last occurrence of the character.\n8. We update the index of the current character in the `charMap` and continue the iteration.\n9. At the end, we return the `maxLength` as the length of the longest substring without repeating characters.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int lengthOfLongestSubstring(string s) {\n int n = s.length();\n int maxLength = 0;\n unordered_map<char, int> charMap;\n int left = 0;\n \n for (int right = 0; right < n; right++) {\n if (charMap.count(s[right]) == 0 || charMap[s[right]] < left) {\n charMap[s[right]] = right;\n maxLength = max(maxLength, right - left + 1);\n } else {\n left = charMap[s[right]] + 1;\n charMap[s[right]] = right;\n }\n }\n \n return maxLength;\n }\n};\n```\n```Java []\nclass Solution {\n public int lengthOfLongestSubstring(String s) {\n int n = s.length();\n int maxLength = 0;\n Map<Character, Integer> charMap = new HashMap<>();\n int left = 0;\n \n for (int right = 0; right < n; right++) {\n if (!charMap.containsKey(s.charAt(right)) || charMap.get(s.charAt(right)) < left) {\n charMap.put(s.charAt(right), right);\n maxLength = Math.max(maxLength, right - left + 1);\n } else {\n left = charMap.get(s.charAt(right)) + 1;\n charMap.put(s.charAt(right), right);\n }\n }\n \n return maxLength;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n n = len(s)\n maxLength = 0\n charMap = {}\n left = 0\n \n for right in range(n):\n if s[right] not in charMap or charMap[s[right]] < left:\n charMap[s[right]] = right\n maxLength = max(maxLength, right - left + 1)\n else:\n left = charMap[s[right]] + 1\n charMap[s[right]] = right\n \n return maxLength\n\n```\n\n# Approach 3 - Integer Array\n1. This solution uses an integer array `charIndex` to store the indices of characters.\n2. We eliminate the need for an unordered map by utilizing the array.\n3. The `maxLength`, `left`, and `right` pointers are still present.\n4. We iterate through the string using the `right` pointer.\n5. We check if the current character has occurred within the current substring by comparing its index in `charIndex` with `left`.\n6. If the character has occurred, we move the `left` pointer to the next position after the last occurrence of the character.\n7. We update the index of the current character in `charIndex`.\n8. At each step, we update the `maxLength` by calculating the length of the current substring.\n9. We continue the iteration until reaching the end of the string.\n10. Finally, we return the `maxLength` as the length of the longest substring without repeating characters.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int lengthOfLongestSubstring(string s) {\n int n = s.length();\n int maxLength = 0;\n vector<int> charIndex(128, -1);\n int left = 0;\n \n for (int right = 0; right < n; right++) {\n if (charIndex[s[right]] >= left) {\n left = charIndex[s[right]] + 1;\n }\n charIndex[s[right]] = right;\n maxLength = max(maxLength, right - left + 1);\n }\n \n return maxLength;\n }\n};\n```\n```Java []\nclass Solution {\n public int lengthOfLongestSubstring(String s) {\n int n = s.length();\n int maxLength = 0;\n int[] charIndex = new int[128];\n Arrays.fill(charIndex, -1);\n int left = 0;\n \n for (int right = 0; right < n; right++) {\n if (charIndex[s.charAt(right)] >= left) {\n left = charIndex[s.charAt(right)] + 1;\n }\n charIndex[s.charAt(right)] = right;\n maxLength = Math.max(maxLength, right - left + 1);\n }\n \n return maxLength;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n n = len(s)\n maxLength = 0\n charIndex = [-1] * 128\n left = 0\n \n for right in range(n):\n if charIndex[ord(s[right])] >= left:\n left = charIndex[ord(s[right])] + 1\n charIndex[ord(s[right])] = right\n maxLength = max(maxLength, right - left + 1)\n \n return maxLength\n\n```\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n\n | 818 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
[VIDEO] Step-by-Step Visualization of Sliding Window | longest-substring-without-repeating-characters | 0 | 1 | https://youtu.be/pY2dYa1m2VM\n\nA brute force solution would first require finding every possible substring, which would run in O(n<sup>2</sup>) time. We\'re not done yet though, because we now have to check every substring for duplicate characters by iterating through every substring. Each check for duplicate characters runs in O(n) time, and we need to do that for every substring generated (which ran in O(n<sup>2</sup>) time), so the brute force approach ends up running in O(n<sup>3</sup>) time.\n\nInstead, we can reduce this to O(n) time by using a sliding window approach and eliminating unnecessary computations. We use two pointers, `l` and `r`, to denote where the substring starts and ends, and a dictionary called `seen` to keep track of the index of each character encountered. Then, we move the right pointer one character at a time to the right to expand our substring.\n\nAt each iteration, we check for two things.\n1. Have we seen the newly added character (at index `r`) before? If we haven\'t, then this is a brand new character and we can just add it to the substring and extend the length\n2. If we have seen it before, is its last known position greater than or equal to the left index? If it is, then that means it\'s repeated somewhere in the substring. If not, then that means it\'s <i>outside</i> of the substring, so we can just add it to the substring and extend the length\n\nSo if both conditions are true, the new character is repeated and we have a problem. We can get rid of the repeated character by moving up the left pointer to be one index past the last recorded index in `seen`. Then, we just keep moving up the right pointer until it reaches the end of the string. Since we only have to loop through the string once, and since hash table lookups run in constant time, this algorithm ends up running in O(n) time.\n\nFor an intuitive proof of why this works and why we don\'t need to check all the other substrings while moving up the left pointer, please see the video - it\'s a bit difficult to explain without a visualization and a concrete example. But basically, all the other substrings will either still contain a repeated character or will be shorter than the last valid substring encountered, so they can be safely ignored.\n\n\n# Code\n```\nclass Solution(object):\n def lengthOfLongestSubstring(self, s):\n seen = {}\n l = 0\n length = 0\n for r in range(len(s)):\n char = s[r]\n if char in seen and seen[char] >= l:\n l = seen[char] + 1\n else:\n length = max(length, r - l + 1)\n seen[char] = r\n\n return length\n``` | 6 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
[Python3]: sliding window O(N) with explanation | longest-substring-without-repeating-characters | 0 | 1 | **Sliding window**\nWe use a dictionary to store the character as the key, the last appear index has been seen so far as value.\nseen[charactor] = index\n\n move the pointer when you met a repeated character in your window.\n\n\t \n```\nindext 0 1 2 3 4 5 6 7\nstring a c b d b a c d\n ^ ^\n | |\n\t\tleft right\n\t\tseen = {a : 0, c : 1, b : 2, d: 3} \n\t\t# case 1: seen[b] = 2, current window is s[0:4] , \n\t\t# b is inside current window, seen[b] = 2 > left = 0. Move left pointer to seen[b] + 1 = 3\n\t\tseen = {a : 0, c : 1, b : 4, d: 3} \nindext 0 1 2 3 4 5 6 7\nstring a c b d b a c d\n\t\t\t\t\t\t ^ ^\n\t\t\t\t\t | |\n\t\t\t\t left right\t\t\nindext 0 1 2 3 4 5 6 7\nstring a c b d b a c d\n\t\t\t\t\t ^ ^\n\t\t\t\t\t | |\n\t\t\t\t left right\t\t\n\t\t# case 2: seen[a] = 0,which means a not in current window s[3:5] , since seen[a] = 0 < left = 3 \n\t\t# we can keep moving right pointer.\n```\n\n```\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n seen = {}\n l = 0\n output = 0\n for r in range(len(s)):\n """\n If s[r] not in seen, we can keep increasing the window size by moving right pointer\n """\n if s[r] not in seen:\n output = max(output,r-l+1)\n """\n There are two cases if s[r] in seen:\n case1: s[r] is inside the current window, we need to change the window by moving left pointer to seen[s[r]] + 1.\n case2: s[r] is not inside the current window, we can keep increase the window\n """\n else:\n if seen[s[r]] < l:\n output = max(output,r-l+1)\n else:\n l = seen[s[r]] + 1\n seen[s[r]] = r\n return output\n```\n* Time complexity :O(n). \n\tn is the length of the input string.\n\tIt will iterate n times to get the result.\n\n* Space complexity: O(m)\n\tm is the number of unique characters of the input. \n\tWe need a dictionary to store unique characters.\n\n | 819 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
👾C#,Java,Python3, JavaScript Solutions (easy) | longest-substring-without-repeating-characters | 1 | 1 | See Code and Explanation : **\u2B50[https://zyrastory.com/en/coding-en/leetcode-en/leetcode-3-longest-substring-without-repeating-characters-solution-and-explanation-en/](https://zyrastory.com/en/coding-en/leetcode-en/leetcode-3-longest-substring-without-repeating-characters-solution-and-explanation-en/)\u2B50**\n\n**Examples : C# - HashSet**\n```\npublic class Solution {\n public int LengthOfLongestSubstring(string s) {\n \n if(string.IsNullOrEmpty(s))\n {\n return 0;\n }\n\n HashSet<char> hSet = new HashSet<char>();\n int max = 0;\n int i = 0;\n int j = 0;\n \n while(i<s.Length)\n {\n if(!hSet.Contains(s[i]))\n {\n hSet.Add(s[i]);\n i++;\n \n }\n else\n {\n max = Math.Max(max,hSet.Count);\n hSet.Remove(s[j]);\n j++;\n }\n }\n max = Math.Max(max,hSet.Count);\n return max;\n \n }\n}\n```\n\n**Examples : C# - Dictionary**\n```\npublic class Solution {\n public int LengthOfLongestSubstring(string s) {\n Dictionary<char,int> dict = new Dictionary<char,int>();\n int max = 0;\n \n for (int i = 0;i < s.Length;i++)\n {\n char c = s[i];\n if (!dict.ContainsKey(c))\n {\n dict.Add(c, i);\n max = Math.Max(dict.Count, max);\n }\n else\n {\n i = dict[c] ;\n dict.Clear();\n }\n }\n return max; \n }\n}\n```\n\n\nIf you got any problem about the explanation or you need other programming language solution, please feel free to leave your comment.\n\n\uD83E\uDDE1See more problems solutions - **[Zyrastory - LeetCode Solution](https://zyrastory.com/en/category/coding-en/leetcode-en/)**\n\nThanks! | 7 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
#Python(🐍) Easy solution O(n) | longest-substring-without-repeating-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n len_sub=[]\n prev=""\n cnt=0\n i=0\n while i <len(s):\n j=i\n cnt=0\n while(j<len(s) and (s[j] not in prev)):\n prev=prev+s[j]\n cnt+=1\n j+=1\n prev=""\n i+=1\n len_sub.append(cnt)\n print(len_sub)\n if(len_sub==[]):\n return 0\n\n return max(len_sub)\n \n\n``` | 1 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
Simple Python3 Solution using Sliding window || Beats 99% || 💻🧑💻🤖 | longest-substring-without-repeating-characters | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n l=len(s)\n if l==0:\n return 0\n dicts={}\n max_len=0\n start=0\n for i in range(l):\n if s[i] in dicts and start<=dicts[s[i]]:\n start = dicts[s[i]]+1\n else:\n max_len=max(max_len,i-start+1)\n dicts[s[i]]=i\n return max_len\n \n```\n\n | 25 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
Simple Explanation | Concise | Thinking Process & Example | longest-substring-without-repeating-characters | 0 | 1 | Lets start with the following example: \n\n**Assume you had no repeating characters** (In below example, just look at *first three* characters)\n\nWe take two pointers, `l` and `r`, both starting at `0`. At every iteration, we update the longest string with non-repeating characters found = `r-l+1` and just keep a note of which character we see at which index\n\n\n<img src="https://assets.leetcode.com/users/images/3e7b9848-1d57-42ed-9629-59f14cfcce89_1595114117.3901849.png" width=400/>\n\n\n```python\n def lengthOfLongestSubstringSimpler(self, s):\n seen = {}\n left, right = 0, 0\n longest = 1\n while right < len(s):\n longest = max(longest, right - left + 1)\n seen[s[right]] = right\n right += 1\n return longest\n```\n\nAfter 3 iterations, if you were keeping a map of when you last saw the character, you\'d have something like this:\n\n<img src="https://assets.leetcode.com/users/images/2f60312a-d377-4786-9449-4a95210f72e2_1595114189.5949714.png" width=300/>\n\nat this point, `longest = r-l+1 = 2 - 0 + 1 = 3`\n\nNow, lets face it - our string _does_ have repeating characters. We look at index 3, we\'re realizing we\'ve seen `a` before. So we now, we can\'t just calculate the value of `longest` like we were doing before. We need to make sure our left pointer, or `l`, is at least past the index where we last saw `a` , thus - we move `l ` to ` seen[right]+1`. We also update our map with last seen of `a` to `3`\n\n<img src="https://assets.leetcode.com/users/images/b7aaad14-993b-47e9-af01-441bbc5dfe20_1595114261.38747.png" width=300/>\n\nAnd this interplay goes on\n\n<img src="https://assets.leetcode.com/users/images/a22de24e-9e66-4e21-ab33-2ac06ce1d0cb_1595114354.4211376.png" width=300/>\n\n\n```python\n def lengthOfLongestSubstring(self, s):\n """\n :type s: str\n :rtype: int \n """\n if len(s) == 0:\n return 0\n seen = {}\n left, right = 0, 0\n longest = 1\n while right < len(s):\n if s[right] in seen:\n left = seen[s[right]]+1\n longest = max(longest, right - left + 1)\n seen[s[right]] = right\n right += 1\n return longest\n```\n\nLife was good, until this test case came into our lives:\n`abba`\n\n<img src="https://assets.leetcode.com/users/images/cce6e442-6d18-4971-bcf2-d2c59ea11a51_1595115276.967406.png" width=200/>\n\nAnd we realised, after 4 iterations, our left pointer was to be moved `seen[s[right]]+1 = seen[a] + 1 = 1` - wait what, left was to move back ? That doesn\'t sound correct - that\'d give us longest to be 3 (bba) which is NOT CORRECT\n\nThus, we need to ensure that `l` always goes to the right of it, or just stays at its position\n\nIn other words;\n\n```python\nclass Solution(object):\n def lengthOfLongestSubstring(self, s):\n """\n :type s: str\n :rtype: int abcabcbb\n """\n if len(s) == 0:\n return 0\n seen = {}\n left, right = 0, 0\n longest = 1\n while right < len(s):\n if s[right] in seen:\n left = max(left,seen[s[right]]+1)\n longest = max(longest, right - left + 1)\n seen[s[right]] = right\n right += 1\n print(left, right, longest)\n return longest\n```\n\nThanks, and don\'t forget to upvote if it helped you !\n\n\n\n**BONUS** Trying to be a strong Java Developer ? Checkout this [awesome hands-on series](https://abhinandandubey.github.io/posts/tags/Advanced-Java-Series) with illustrations! \n | 348 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
🔥🔥🔥 python3 Easy ( Sliding window Technique )🔥🔥🔥 | longest-substring-without-repeating-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n start=0\n count=0\n for end in range(1,len(s)+1):\n if len(set(s[start:end]))==len(s[start:end]):\n if (end-start+1)>count:\n count=len(s[start:end])\n else:\n start+=1\n return(count)\n\n``` | 9 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
beats 99.72% on time and 88.23% on space | longest-substring-without-repeating-characters | 0 | 1 | # Approach\n\nUse a two-pointer approach and maintain a set of unique characters between the two pointers. iterate through string, checking if the next char is unique or not. If it\'s unique, add it to unique chars and advance the leading index. Otherwise, advance the trailing index until the unique chars set is exclusively unique chars. Either way, maintain uniqueChars set to correctly represent the chars between leading and trailing indices. \n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n\n\n# Code\n```\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n # two pointer solution and a set TC O(n), SC O(n)\n # if len(s) is 0 or 1, return it\n if len(s) < 2:\n return len(s)\n\n # init the 2 pointers and keep track of a set of unqiue chars in between [trailingI, leadingI)\n\n trailingI, leadingI = len(s) - 1, len(s) - 2\n uniqueChars = {s[len(s) - 1]}\n result = setSize = 1\n\n while leadingI > -1:\n newChar = s[leadingI]\n if newChar in uniqueChars:\n # advance leftI until it\'s at the previous instance of newChar\n while (s[trailingI] != newChar):\n uniqueChars.remove(s[trailingI])\n setSize -= 1\n trailingI -= 1\n \n # advance both indices\n trailingI -= 1\n leadingI -= 1\n\n else:\n # this char is unique, add it to the set, check the new set size, and advance leadingI\n uniqueChars.add(newChar)\n setSize += 1\n result = max(result, setSize)\n leadingI -= 1\n\n return result\n\n # if there is time...\n # there is a solution to do this in TC O(n), SC O(1) by removing elements from s while we go (destroys s)\n\n # modify algo to go right to left\n # whenever we move rightI (trailingI), delete the elements behind it\n\n``` | 0 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
Beats 98.7%✅ | O( O(n^2 )✅ | Python (Step by step explanation) | longest-substring-without-repeating-characters | 0 | 1 | # Intuition\nThe problem requires finding the length of the longest substring without repeating characters in a given string. We can approach this by using a sliding window technique to keep track of the current substring without repeating characters and update the maximum length found so far.\n\n# Approach\n1. Initialize two empty strings, `temp` and `ans`, to store the current substring and the longest substring found.\n2. Iterate through each character `i` in the input string `s`.\n3. If `i` is not in the `temp` substring, append it to `temp` to extend the current substring.\n4. If `i` is already in `temp`, it means a repeating character is found. \n - Find the index of the first occurrence of `i` in `temp`.\n - Update `ans` with the longer of `temp` and the previously stored `ans`.\n - Adjust `temp` by removing characters from the beginning up to and including the first occurrence of `i` and then append `i`.\n5. After processing all characters in the input string, check one last time to update `ans` with the longest substring if it ends at the end of the input string.\n6. Return the length of the longest substring found, which is stored in `ans`.\n\n# Complexity\n- Time complexity: O(n^2), where n is the length of the input string `s`. We iterate through the string once.\n- Space complexity: O(min(n, m)), where m is the size of the character set. In the worst case, the entire string is unique (no repeating characters), and both `temp` and `ans` can have a maximum size of n. In practice, space complexity may be smaller depending on the input.\n\n\n# Code\n```\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n temp =""\n ans = ""\n for i in s:\n if i not in temp:\n temp += i\n else:\n ind = temp.index(i)\n ans = temp if len(temp)>len(ans) else ans\n temp = temp[ind + 1:]\n temp += i\n ans = temp if len(temp) > len(ans) else ans \n\n return len(ans) \n \n```\n\n# Please upvote the solution if you understood it.\n\n | 2 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
Sliding Window Approach (Runtime - beats 94.47%) | Time Complexity O(n) | longest-substring-without-repeating-characters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this code is to use a sliding window approach to maintain a substring that doesn\'t contain repeating characters. By keeping track of the most recent index where each character appeared, the algorithm can efficiently adjust the starting point of the current substring when a repeating character is encountered.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code uses a sliding window approach with two pointers, `start` and `end`, that define the current substring without repeating characters. The `char_index` dictionary is used to store the most recent index where each character appeared.\n\n- For each character encountered, the code checks if the character is already in `char_index` and if its index is greater than or equal to the current `start` index. If so, it means that the character has appeared previously in the current substring. In this case, the `start` index is moved to the position immediately after the last occurrence of the character.\n- The `char_index` dictionary is updated with the current character\'s index.\n- The length of the current substring is calculated using `end - start + 1`, and the `max_length` is updated if necessary.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(min(n, m)) - where n is the length of the input string and m is the size of the character set (number of distinct characters in the input string).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n if not s:\n return 0\n char_index = {} \n start = 0 \n max_length = 0 \n for end, char in enumerate(s):\n if char in char_index and char_index[char] >= start:\n start = char_index[char] + 1\n \n char_index[char] = end\n max_length = max(max_length, end - start + 1)\n \n return max_length\n \n``` | 4 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
Easy well explained python solution (faster than 98%), O(n) time complexity | longest-substring-without-repeating-characters | 0 | 1 | # Intuition\nwe use a **starting point** while iterating over the given string and every time we find a repeated character we calculate the length of the substring between the starting point and the current point - 1.\nevery time we find a repetition we set the starting point to the character next to the last occurrence.\n\n**Ex :** consider the string **`abcdae`**\n\nthe starting point will be $$0$$ initially, we keep iterating until we find the second **`a`**. we calculate then the length of the substring **`abcd`** and then set the starting point to the character next to the first **`a`**, which is **`b`**.\nthen, we will keep iterating until the end since there are no more repetitions and the answer will be $$5$$ (the length of **`bcdae`**).\n\n# Approach\nwe will need $$2$$ variables: \n1. $$`longest`$$ to **save the length of the longest substring found**\n2. $$`offset`$$ for **the starting point**.\n\nwe will also need to save the encountered characters to check repetition, a dictionary will be ideal for this case as it doesn\'t allow repetition. for that we will use an extra variable \n- $$`indexes`$$: to save characters and their indexes, **characters** will be **keys** and **indexes** will be **values**.\n\nwe start then: for every character: \n1. we get its index from indexes dictionary.\n2. if the index wasn\'t null `(meaning that it was encountered before)`, we check if its index is **greater or equal to the offset** `(meaning that its in the current substring)`.\nif so :\n - we calculate the length of the substring : $$i\\,(current\\: position) - offset$$\n - we set the offset to the next character of the last occurrence : $$index\\,(last\\:occurrence) + 1$$\n - if the length of this substring is greater than the length of the current longest substring, we update it\n3. we update the index of the last occurrence of the current character (or add it if this is its first occurrence).\n\nFinally, we return the **maximum** between $$`longest`$$ and **the length of the last substring** `(which is equal to the difference between the length of the string and offset)`as it contains **no repeated characters** and its length is **never compared** to $$`longest`$$ because **we get out of the loop**.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def lengthOfLongestSubstring(self, s: str) -> int:\n longest = 0\n indexes = {}\n offset = 0\n for i in range(len(s)):\n char = s[i]\n index = indexes.get(char)\n if index is not None and index >= offset:\n length = i - offset\n offset = index + 1\n if length > longest:\n longest = length\n indexes[char] = i\n return max(longest, (len(s) - offset))\n``` | 12 | Given a string `s`, find the length of the **longest** **substring** without repeating characters.
**Example 1:**
**Input:** s = "abcabcbb "
**Output:** 3
**Explanation:** The answer is "abc ", with the length of 3.
**Example 2:**
**Input:** s = "bbbbb "
**Output:** 1
**Explanation:** The answer is "b ", with the length of 1.
**Example 3:**
**Input:** s = "pwwkew "
**Output:** 3
**Explanation:** The answer is "wke ", with the length of 3.
Notice that the answer must be a substring, "pwke " is a subsequence and not a substring.
**Constraints:**
* `0 <= s.length <= 5 * 104`
* `s` consists of English letters, digits, symbols and spaces. | null |
✅ [video walkthrough] 🔥 Readable code explained by FAANG engineer | median-of-two-sorted-arrays | 0 | 1 | I made a super detailed video walkthrough, since this is a really tough question \uD83D\uDE42 \nPlease upvote if you find this helpful!\n\nhttps://youtu.be/QjrchMRAkew\n\nCode:\n```\nclass Solution:\n def findMedianSortedArrays(self, nums1, nums2):\n if len(nums1) > len(nums2):\n nums1, nums2 = nums2, nums1\n \n m, n = len(nums1), len(nums2)\n left, right = 0, m\n N = m + n\n\n while left <= right:\n A = (left + right) // 2\n B = ((N + 1) // 2) - A\n\n x1 = -float("inf") if A - 1 < 0 else nums1[A - 1]\n y1 = float("inf") if A == m else nums1[A]\n x2 = -float("inf") if B - 1 < 0 else nums2[B - 1]\n y2 = float("inf") if B == n else nums2[B]\n\n if x1 <= y2 and x2 <= y1:\n if N % 2 == 0:\n return (max(x1, x2) + min(y1, y2)) / 2\n else:\n return max(x1, x2)\n elif x1 > y2:\n right = A - 1\n else:\n left = A + 1\n``` | 59 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
✅99%🔥||✅Journey From Brute Force to Most 🔥Optimized ✅Three Approaches||🔥Easy to understand | median-of-two-sorted-arrays | 1 | 1 | # Problem Understanding:\nIn simpler terms, you need to **find the middle value of the combined**, sorted array formed by merging nums1 and nums2. If the combined **array has an even number** of elements, you should return the average of the two middle values. **If it has an odd number of elements, you should return the middle value itself.**\n<!-- Describe your first thoughts on how to solve this problem. -->\n# Hint:\n```Hint1 []\nThink of a brute force approach.\n```\n```Hint2 []\nDo you think how two pointer will help us?\n```\n```Hint3 []\nCan you observe the fact that the given arrays are sorted?\n```\n**I would recommend you, don\'t jump directly on solution.**\n# Approach 1: Merge and Sort\n- **Create a new array** with a size equal to the total number of elements in both input arrays.\n- **Insert elements** from both input arrays into the new array.\n- **Sort the new array.**\n- **Find and return the median of the sorted array.**\n\n**Time Complexity**\n- In the worst case TC is **O((n + m) * log(n + m))**.\n\n**Space Complexity**\n - **O(n + m)**, where \u2018n\u2019 and \u2018m\u2019 are the sizes of the arrays.\n# Approach 2: Two-Pointer Method\n\n- **Initialize two pointers**, i and j, both initially set to 0.\n- **Move the pointer** that corresponds to the **smaller value forward at each step.**\n- Continue moving the pointers **until you have processed half of the total number of elements.**\n- Calculate and **return the median** based on the values pointed to by i and j.\n\n\n**Time Complexity**\n- **O(n + m)**, where \u2018n\u2019 & \u2018m\u2019 are the sizes of the two arrays.\n\n**Space Complexity**\n - **O(1)**.\n\n# Approach 3: Binary Search\n\n- **Use binary search to partition the smaller of the two input arrays into two parts.**\n- Find the partition of the **larger array such that the sum of elements on the left side of the partition in both arrays is half of the total elements.**\n- Check if this partition **is valid by verifying** if the largest number on the left side is smaller than the smallest number on the right side.\n- **If the partition is valid,** calculate and return the median.\n\n**Time Complexity**\n- **O(logm/logn)**\n\n**Space Complexity**\n - **O(1)**\n\n---\n\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n---\n\n\n<!-- Describe your approach to solving the problem. -->\n# Code Brute Force- Merge and Sort\n```C++ []\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n // Get the sizes of both input arrays.\n int n = nums1.size();\n int m = nums2.size();\n\n // Merge the arrays into a single sorted array.\n vector<int> merged;\n for (int i = 0; i < n; i++) {\n merged.push_back(nums1[i]);\n }\n for (int i = 0; i < m; i++) {\n merged.push_back(nums2[i]);\n }\n\n // Sort the merged array.\n sort(merged.begin(), merged.end());\n\n // Calculate the total number of elements in the merged array.\n int total = merged.size();\n\n if (total % 2 == 1) {\n // If the total number of elements is odd, return the middle element as the median.\n return static_cast<double>(merged[total / 2]);\n } else {\n // If the total number of elements is even, calculate the average of the two middle elements as the median.\n int middle1 = merged[total / 2 - 1];\n int middle2 = merged[total / 2];\n return (static_cast<double>(middle1) + static_cast<double>(middle2)) / 2.0;\n }\n }\n};\n\n```\n```Java []\nimport java.util.Arrays;\n\nclass Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n // Get the sizes of both input arrays.\n int n = nums1.length;\n int m = nums2.length;\n\n // Merge the arrays into a single sorted array.\n int[] merged = new int[n + m];\n int k = 0;\n for (int i = 0; i < n; i++) {\n merged[k++] = nums1[i];\n }\n for (int i = 0; i < m; i++) {\n merged[k++] = nums2[i];\n }\n\n // Sort the merged array.\n Arrays.sort(merged);\n\n // Calculate the total number of elements in the merged array.\n int total = merged.length;\n\n if (total % 2 == 1) {\n // If the total number of elements is odd, return the middle element as the median.\n return (double) merged[total / 2];\n } else {\n // If the total number of elements is even, calculate the average of the two middle elements as the median.\n int middle1 = merged[total / 2 - 1];\n int middle2 = merged[total / 2];\n return ((double) middle1 + (double) middle2) / 2.0;\n }\n }\n}\n\n```\n```python3 []\nclass Solution:\n def findMedianSortedArrays(self, nums1, nums2):\n # Merge the arrays into a single sorted array.\n merged = nums1 + nums2\n\n # Sort the merged array.\n merged.sort()\n\n # Calculate the total number of elements in the merged array.\n total = len(merged)\n\n if total % 2 == 1:\n # If the total number of elements is odd, return the middle element as the median.\n return float(merged[total // 2])\n else:\n # If the total number of elements is even, calculate the average of the two middle elements as the median.\n middle1 = merged[total // 2 - 1]\n middle2 = merged[total // 2]\n return (float(middle1) + float(middle2)) / 2.0\n\n```\n\n\n# Code for Two-Pointer Method\n```C++ []\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n int m = nums2.size();\n int i = 0, j = 0, m1 = 0, m2 = 0;\n\n // Find median.\n for (int count = 0; count <= (n + m) / 2; count++) {\n m2 = m1;\n if (i != n && j != m) {\n if (nums1[i] > nums2[j]) {\n m1 = nums2[j++];\n } else {\n m1 = nums1[i++];\n }\n } else if (i < n) {\n m1 = nums1[i++];\n } else {\n m1 = nums2[j++];\n }\n }\n\n // Check if the sum of n and m is odd.\n if ((n + m) % 2 == 1) {\n return static_cast<double>(m1);\n } else {\n double ans = static_cast<double>(m1) + static_cast<double>(m2);\n return ans / 2.0;\n }\n }\n};\n\n```\n```Java []\nclass Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n int n = nums1.length;\n int m = nums2.length;\n int i = 0, j = 0, m1 = 0, m2 = 0;\n\n // Find median.\n for (int count = 0; count <= (n + m) / 2; count++) {\n m2 = m1;\n if (i != n && j != m) {\n if (nums1[i] > nums2[j]) {\n m1 = nums2[j++];\n } else {\n m1 = nums1[i++];\n }\n } else if (i < n) {\n m1 = nums1[i++];\n } else {\n m1 = nums2[j++];\n }\n }\n\n // Check if the sum of n and m is odd.\n if ((n + m) % 2 == 1) {\n return (double) m1;\n } else {\n double ans = (double) m1 + (double) m2;\n return ans / 2.0;\n }\n }\n}\n\n```\n```python []\nclass Solution:\n def findMedianSortedArrays(self, nums1, nums2):\n n = len(nums1)\n m = len(nums2)\n i = 0\n j = 0\n m1 = 0\n m2 = 0\n\n # Find median.\n for count in range(0, (n + m) // 2 + 1):\n m2 = m1\n if i < n and j < m:\n if nums1[i] > nums2[j]:\n m1 = nums2[j]\n j += 1\n else:\n m1 = nums1[i]\n i += 1\n elif i < n:\n m1 = nums1[i]\n i += 1\n else:\n m1 = nums2[j]\n j += 1\n\n # Check if the sum of n and m is odd.\n if (n + m) % 2 == 1:\n return float(m1)\n else:\n ans = float(m1) + float(m2)\n return ans / 2.0\n\n```\n\n\n# Code for Binary Search\n```C++ []\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int> &nums1, vector<int> &nums2) {\n int n1 = nums1.size(), n2 = nums2.size();\n \n // Ensure nums1 is the smaller array for simplicity\n if (n1 > n2)\n return findMedianSortedArrays(nums2, nums1);\n \n int n = n1 + n2;\n int left = (n1 + n2 + 1) / 2; // Calculate the left partition size\n int low = 0, high = n1;\n \n while (low <= high) {\n int mid1 = (low + high) >> 1; // Calculate mid index for nums1\n int mid2 = left - mid1; // Calculate mid index for nums2\n \n int l1 = INT_MIN, l2 = INT_MIN, r1 = INT_MAX, r2 = INT_MAX;\n \n // Determine values of l1, l2, r1, and r2\n if (mid1 < n1)\n r1 = nums1[mid1];\n if (mid2 < n2)\n r2 = nums2[mid2];\n if (mid1 - 1 >= 0)\n l1 = nums1[mid1 - 1];\n if (mid2 - 1 >= 0)\n l2 = nums2[mid2 - 1];\n \n if (l1 <= r2 && l2 <= r1) {\n // The partition is correct, we found the median\n if (n % 2 == 1)\n return max(l1, l2);\n else\n return ((double)(max(l1, l2) + min(r1, r2))) / 2.0;\n }\n else if (l1 > r2) {\n // Move towards the left side of nums1\n high = mid1 - 1;\n }\n else {\n // Move towards the right side of nums1\n low = mid1 + 1;\n }\n }\n \n return 0; // If the code reaches here, the input arrays were not sorted.\n }\n};\n\n\n```\n```Java []\nclass Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n int n1 = nums1.length, n2 = nums2.length;\n \n // Ensure nums1 is the smaller array for simplicity\n if (n1 > n2)\n return findMedianSortedArrays(nums2, nums1);\n \n int n = n1 + n2;\n int left = (n1 + n2 + 1) / 2; // Calculate the left partition size\n int low = 0, high = n1;\n \n while (low <= high) {\n int mid1 = (low + high) >> 1; // Calculate mid index for nums1\n int mid2 = left - mid1; // Calculate mid index for nums2\n \n int l1 = Integer.MIN_VALUE, l2 = Integer.MIN_VALUE, r1 = Integer.MAX_VALUE, r2 = Integer.MAX_VALUE;\n \n // Determine values of l1, l2, r1, and r2\n if (mid1 < n1)\n r1 = nums1[mid1];\n if (mid2 < n2)\n r2 = nums2[mid2];\n if (mid1 - 1 >= 0)\n l1 = nums1[mid1 - 1];\n if (mid2 - 1 >= 0)\n l2 = nums2[mid2 - 1];\n \n if (l1 <= r2 && l2 <= r1) {\n // The partition is correct, we found the median\n if (n % 2 == 1)\n return Math.max(l1, l2);\n else\n return ((double)(Math.max(l1, l2) + Math.min(r1, r2))) / 2.0;\n }\n else if (l1 > r2) {\n // Move towards the left side of nums1\n high = mid1 - 1;\n }\n else {\n // Move towards the right side of nums1\n low = mid1 + 1;\n }\n }\n \n return 0; // If the code reaches here, the input arrays were not sorted.\n }\n}\n\n```\n```python []\nclass Solution:\n def findMedianSortedArrays(self, nums1, nums2):\n n1 = len(nums1)\n n2 = len(nums2)\n \n # Ensure nums1 is the smaller array for simplicity\n if n1 > n2:\n return self.findMedianSortedArrays(nums2, nums1)\n \n n = n1 + n2\n left = (n1 + n2 + 1) // 2 # Calculate the left partition size\n low = 0\n high = n1\n \n while low <= high:\n mid1 = (low + high) // 2 # Calculate mid index for nums1\n mid2 = left - mid1 # Calculate mid index for nums2\n \n l1 = float(\'-inf\')\n l2 = float(\'-inf\')\n r1 = float(\'inf\')\n r2 = float(\'inf\')\n \n # Determine values of l1, l2, r1, and r2\n if mid1 < n1:\n r1 = nums1[mid1]\n if mid2 < n2:\n r2 = nums2[mid2]\n if mid1 - 1 >= 0:\n l1 = nums1[mid1 - 1]\n if mid2 - 1 >= 0:\n l2 = nums2[mid2 - 1]\n \n if l1 <= r2 and l2 <= r1:\n # The partition is correct, we found the median\n if n % 2 == 1:\n return max(l1, l2)\n else:\n return (max(l1, l2) + min(r1, r2)) / 2.0\n elif l1 > r2:\n # Move towards the left side of nums1\n high = mid1 - 1\n else:\n # Move towards the right side of nums1\n low = mid1 + 1\n \n return 0 # If the code reaches here, the input arrays were not sorted.\n\n```\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A\n\n\n\n | 802 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
🔥99% || Super easy🔥👌 | median-of-two-sorted-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Combine the two input arrays \'nums1\' and \'nums2\' into a single array named \'nums\'.\n2. Sort the combined array \'nums\' in ascending order.\n3. Determine the length of the sorted array \'nums\'.\n4. If the length \'n\' is even, calculate the median as the average of the two middle elements.\n5. If the length \'n\' is odd, simply take the middle element as the median.\n6. Round the calculated median to 5 decimal places.\n7. Return the rounded median as a float.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n log n).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n nums = (nums1 + nums2)\n nums.sort()\n n = len(nums)\n if n%2 == 0:\n res = n//2\n return round((nums[res-1]+nums[res])/2,5)\n else:\n res = n//2\n return round(nums[res],5)\n \n``` | 1 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
Median of Two Sorted Arrays | Optimal Code | Python | | median-of-two-sorted-arrays | 0 | 1 | # Complexity\n- Time complexity: $$O(log(n + m))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n n1 = len(nums1)\n n2 = len(nums2)\n if n1 > n2:\n return self.findMedianSortedArrays(nums2, nums1)\n n = n1 + n2\n left = (n + 1) // 2\n low = 0\n high = n1\n while low <= high:\n mid1 = (low + high) // 2\n mid2 = left - mid1\n l1, l2, r1, r2 = float("-inf"), float("-inf"), float("inf"), float("inf")\n if mid1 < n1: r1 = nums1[mid1]\n if mid2 < n2: r2 = nums2[mid2]\n if mid1 - 1 >= 0: l1 = nums1[mid1 - 1]\n if mid2 - 1 >= 0: l2 = nums2[mid2 - 1]\n if l1 <= r2 and l2 <= r1:\n if n % 2 == 1: return max(l1, l2)\n else: return (float(max(l1, l2)) + float(min(r1, r2))) / 2.0\n if l1 > r2: high = mid1 - 1\n else: low = mid1 + 1\n return 0\n\n\n``` | 1 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
✅ 94.96% Binary Search & Two Pointers | median-of-two-sorted-arrays | 1 | 1 | # Comprehensive Guide to Solving "Median of Two Sorted Arrays"\n\n## Introduction & Problem Statement\n\n"Median of Two Sorted Arrays" is a classic problem that tests one\'s algorithmic depth and understanding of binary search and two-pointer techniques. The challenge is to find the median of two sorted arrays, `nums1` and `nums2`, with potentially different sizes. The objective is to solve it in logarithmic time complexity in terms of the minimum size of the two arrays.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Array Constraints**: \n - The length of `nums1` (denoted as $$ m $$) can range from 0 to 1000.\n - The length of `nums2` (denoted as $$ n $$) can also vary between 0 and 1000.\n - The combined size (i.e., $$ m + n $$) of both arrays can go up to 2000.\n \n2. **Element Constraints**:\n - Each element in both `nums1` and `nums2` can be any integer from -$$ 10^6 $$ to $$ 10^6 $$.\n\n3. **Runtime Complexity**: \n The primary challenge is to achieve a runtime of $$ O(\\log(\\min(m, n))) $$. This constraint rules out naive solutions that might merge and then find the median.\n\n### Solution Strategies:\n\n1. **Two Pointers Approach**: \n This technique involves iterating through both arrays using two pointers. By comparing the elements at the current pointers, we can merge the two arrays. Once merged, finding the median is straightforward.\n\n2. **Binary Search Approach**: \n Leveraging the properties of sorted arrays, we can apply a binary search on the smaller array, effectively partitioning both arrays. This method ensures we find the median without explicitly merging the arrays, adhering to the desired logarithmic time complexity.\n\n---\n\n## Live Coding Binary Search & Explain \nhttps://youtu.be/9LZcuEBjD9o?si=5A6xTTLfH0HW0kal\n\n## Strategy to Solve the Problem:\n\n## Two Pointers Merging Technique\n\nThe core idea here is to merge the two sorted arrays, nums1 and nums2, using a two-pointer approach. After merging, the median of the combined array can be found directly based on its length.\n\n## Key Data Structures:\n\n- `merged`: An array to store the merged result of `nums1` and `nums2`.\n- `i` and `j`: Two pointers to traverse `nums1` and `nums2` respectively.\n\n## Enhanced Breakdown:\n\n1. **Initialize Pointers**:\n - Set `i` and `j` to 0. These pointers will help traverse `nums1` and `nums2`.\n\n2. **Merging using Two Pointers**:\n - Merge elements of `nums1` and `nums2` in sorted order using two pointers. If an element in `nums1` is smaller, append it to `merged` and move the `i` pointer. Otherwise, append the element from `nums2` and move the `j` pointer.\n\n3. **Handle Remaining Elements**:\n - If there are any remaining elements in `nums1` or `nums2`, append them directly to `merged`.\n\n4. **Calculate Median**:\n - Based on the length of `merged`, compute the median. If the length is even, the median is the average of the two middle elements. Otherwise, it\'s the middle element.\n\n## Complexity Analysis:\n\n**Time Complexity**: \n- The merging process traverses both arrays once, resulting in a time complexity of $$ O(m + n) $$, where $$ m $$ and $$ n $$ are the lengths of `nums1` and `nums2` respectively.\n\n**Space Complexity**: \n- The algorithm creates a merged array of length $$ m + n $$, leading to a space complexity of $$ O(m + n) $$.\n\n\n## Code Two Pointers\n``` Python []\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n merged = []\n i, j = 0, 0\n \n while i < len(nums1) and j < len(nums2):\n if nums1[i] < nums2[j]:\n merged.append(nums1[i])\n i += 1\n else:\n merged.append(nums2[j])\n j += 1\n \n while i < len(nums1):\n merged.append(nums1[i])\n i += 1\n \n while j < len(nums2):\n merged.append(nums2[j])\n j += 1\n \n mid = len(merged) // 2\n if len(merged) % 2 == 0:\n return (merged[mid-1] + merged[mid]) / 2\n else:\n return merged[mid]\n\n```\n``` Go []\nfunc findMedianSortedArrays(nums1 []int, nums2 []int) float64 {\n merged := make([]int, 0, len(nums1)+len(nums2))\n i, j := 0, 0\n\n for i < len(nums1) && j < len(nums2) {\n if nums1[i] < nums2[j] {\n merged = append(merged, nums1[i])\n i++\n } else {\n merged = append(merged, nums2[j])\n j++\n }\n }\n\n for i < len(nums1) {\n merged = append(merged, nums1[i])\n i++\n }\n for j < len(nums2) {\n merged = append(merged, nums2[j])\n j++\n }\n\n mid := len(merged) / 2\n if len(merged)%2 == 0 {\n return (float64(merged[mid-1]) + float64(merged[mid])) / 2.0\n } else {\n return float64(merged[mid])\n }\n}\n```\n``` Rust []\nimpl Solution {\n pub fn find_median_sorted_arrays(nums1: Vec<i32>, nums2: Vec<i32>) -> f64 {\n let mut merged: Vec<i32> = Vec::new();\n let (mut i, mut j) = (0, 0);\n \n while i < nums1.len() && j < nums2.len() {\n if nums1[i] < nums2[j] {\n merged.push(nums1[i]);\n i += 1;\n } else {\n merged.push(nums2[j]);\n j += 1;\n }\n }\n \n while i < nums1.len() {\n merged.push(nums1[i]);\n i += 1;\n }\n while j < nums2.len() {\n merged.push(nums2[j]);\n j += 1;\n }\n \n let mid = merged.len() / 2;\n if merged.len() % 2 == 0 {\n return (merged[mid-1] + merged[mid]) as f64 / 2.0;\n } else {\n return merged[mid] as f64;\n }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n vector<int> merged;\n int i = 0, j = 0;\n \n while (i < nums1.size() && j < nums2.size()) {\n if (nums1[i] < nums2[j]) {\n merged.push_back(nums1[i++]);\n } else {\n merged.push_back(nums2[j++]);\n }\n }\n \n while (i < nums1.size()) merged.push_back(nums1[i++]);\n while (j < nums2.size()) merged.push_back(nums2[j++]);\n \n int mid = merged.size() / 2;\n if (merged.size() % 2 == 0) {\n return (merged[mid-1] + merged[mid]) / 2.0;\n } else {\n return merged[mid];\n }\n }\n};\n```\n``` Java []\npublic class Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n List<Integer> merged = new ArrayList<>();\n int i = 0, j = 0;\n \n while (i < nums1.length && j < nums2.length) {\n if (nums1[i] < nums2[j]) {\n merged.add(nums1[i++]);\n } else {\n merged.add(nums2[j++]);\n }\n }\n \n while (i < nums1.length) merged.add(nums1[i++]);\n while (j < nums2.length) merged.add(nums2[j++]);\n \n int mid = merged.size() / 2;\n if (merged.size() % 2 == 0) {\n return (merged.get(mid-1) + merged.get(mid)) / 2.0;\n } else {\n return merged.get(mid);\n }\n }\n}\n```\n``` C# []\npublic class Solution {\n public double FindMedianSortedArrays(int[] nums1, int[] nums2) {\n List<int> merged = new List<int>();\n int i = 0, j = 0;\n \n while (i < nums1.Length && j < nums2.Length) {\n if (nums1[i] < nums2[j]) {\n merged.Add(nums1[i++]);\n } else {\n merged.Add(nums2[j++]);\n }\n }\n \n while (i < nums1.Length) merged.Add(nums1[i++]);\n while (j < nums2.Length) merged.Add(nums2[j++]);\n \n int mid = merged.Count / 2;\n if (merged.Count % 2 == 0) {\n return (merged[mid-1] + merged[mid]) / 2.0;\n } else {\n return merged[mid];\n }\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums1\n * @param {number[]} nums2\n * @return {number}\n */\nvar findMedianSortedArrays = function(nums1, nums2) {\n let merged = [];\n let i = 0, j = 0;\n\n while (i < nums1.length && j < nums2.length) {\n if (nums1[i] < nums2[j]) {\n merged.push(nums1[i++]);\n } else {\n merged.push(nums2[j++]);\n }\n }\n\n while (i < nums1.length) merged.push(nums1[i++]);\n while (j < nums2.length) merged.push(nums2[j++]);\n\n let mid = Math.floor(merged.length / 2);\n if (merged.length % 2 === 0) {\n return (merged[mid-1] + merged[mid]) / 2;\n } else {\n return merged[mid];\n }\n};\n```\n``` PHP []\nclass Solution {\n\n function findMedianSortedArrays($nums1, $nums2) {\n $merged = array();\n $i = $j = 0;\n\n while ($i < count($nums1) && $j < count($nums2)) {\n if ($nums1[$i] < $nums2[$j]) {\n array_push($merged, $nums1[$i++]);\n } else {\n array_push($merged, $nums2[$j++]);\n }\n }\n\n while ($i < count($nums1)) array_push($merged, $nums1[$i++]);\n while ($j < count($nums2)) array_push($merged, $nums2[$j++]);\n\n $mid = intdiv(count($merged), 2);\n if (count($merged) % 2 == 0) {\n return ($merged[$mid-1] + $merged[$mid]) / 2;\n } else {\n return $merged[$mid];\n }\n }\n}\n```\n\n---\n\n## Binary Search with Partitioning\n\nThe problem can be elegantly solved using binary search by partitioning the two arrays such that elements on the left are smaller or equal to elements on the right.\n\n## Key Data Structures:\n\n- `partitionX` and `partitionY`: To store the partition indices for `nums1` and `nums2` respectively.\n- `maxX`, `minX`, `maxY`, `minY`: To store the values around the partition in both arrays.\n\n## Enhanced Breakdown:\n\n1. **Initialize and Swap Arrays if Needed**:\n - Swap `nums1` and `nums2` if `nums1` is larger. This ensures we always binary search the smaller array, optimizing the time complexity.\n\n2. **Binary Search Setup**:\n - Initialize `low` to 0 and `high` to the size of the smaller array.\n \n3. **Start Binary Search Loop**:\n - The loop continues until `low` is not greater than `high`.\n - Calculate `partitionX` and `partitionY` based on `low` and `high`.\n\n4. **Calculate Partition Values**:\n - Compute `maxX`, `minX`, `maxY`, `minY` based on the partitions.\n \n5. **Check for Correct Partition**:\n - If `maxX <= minY` and `maxY <= minX`, we have found the correct partition.\n - Calculate and return the median based on the values around the partition.\n\n6. **Adjust Binary Search Bounds**:\n - If `maxX > minY`, adjust `high` to `partitionX - 1`.\n - Otherwise, adjust `low` to `partitionX + 1`.\n\n## Complexity Analysis:\n\n**Time Complexity**: \n- The algorithm performs a binary search on the smaller array, leading to a time complexity of $$ O(\\log(\\min(m, n))) $$.\n\n**Space Complexity**: \n- The algorithm uses only a constant amount of extra space, thus having a space complexity of $$ O(1) $$.\n\n# Code Binary Search\n``` Python []\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n if len(nums1) > len(nums2):\n nums1, nums2 = nums2, nums1\n \n m, n = len(nums1), len(nums2)\n low, high = 0, m\n \n while low <= high:\n partitionX = (low + high) // 2\n partitionY = (m + n + 1) // 2 - partitionX\n \n maxX = float(\'-inf\') if partitionX == 0 else nums1[partitionX - 1]\n maxY = float(\'-inf\') if partitionY == 0 else nums2[partitionY - 1]\n minX = float(\'inf\') if partitionX == m else nums1[partitionX]\n minY = float(\'inf\') if partitionY == n else nums2[partitionY]\n \n if maxX <= minY and maxY <= minX:\n if (m + n) % 2 == 0:\n return (max(maxX, maxY) + min(minX, minY)) / 2\n else:\n return max(maxX, maxY)\n elif maxX > minY:\n high = partitionX - 1\n else:\n low = partitionX + 1\n```\n``` Go []\nfunc findMedianSortedArrays(nums1 []int, nums2 []int) float64 {\n\tif len(nums1) > len(nums2) {\n\t\tnums1, nums2 = nums2, nums1\n\t}\n\n\tm, n := len(nums1), len(nums2)\n\tlow, high := 0, m\n\n\tfor low <= high {\n\t\tpartitionX := (low + high) / 2\n\t\tpartitionY := (m + n + 1) / 2 - partitionX\n\n\t\tmaxX := math.MinInt64\n\t\tif partitionX > 0 {\n\t\t\tmaxX = nums1[partitionX-1]\n\t\t}\n\n\t\tminX := math.MaxInt64\n\t\tif partitionX < m {\n\t\t\tminX = nums1[partitionX]\n\t\t}\n\n\t\tmaxY := math.MinInt64\n\t\tif partitionY > 0 {\n\t\t\tmaxY = nums2[partitionY-1]\n\t\t}\n\n\t\tminY := math.MaxInt64\n\t\tif partitionY < n {\n\t\t\tminY = nums2[partitionY]\n\t\t}\n\n\t\tif maxX <= minY && maxY <= minX {\n\t\t\tif (m+n)%2 == 0 {\n\t\t\t\treturn (float64(max(maxX, maxY)) + float64(min(minX, minY))) / 2.0\n\t\t\t}\n\t\t\treturn float64(max(maxX, maxY))\n\t\t} else if maxX > minY {\n\t\t\thigh = partitionX - 1\n\t\t} else {\n\t\t\tlow = partitionX + 1\n\t\t}\n\t}\n\n\treturn 0.0\n}\n\nfunc max(a, b int) int {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\n\nfunc min(a, b int) int {\n\tif a < b {\n\t\treturn a\n\t}\n\treturn b\n}\n```\n``` Rust []\nimpl Solution {\n pub fn find_median_sorted_arrays(nums1: Vec<i32>, nums2: Vec<i32>) -> f64 {\n let (mut nums1, mut nums2) = if nums1.len() > nums2.len() {\n (nums2, nums1)\n } else {\n (nums1, nums2)\n };\n \n let (m, n) = (nums1.len(), nums2.len());\n let (mut low, mut high) = (0, m);\n \n while low <= high {\n let partition_x = (low + high) / 2;\n let partition_y = (m + n + 1) / 2 - partition_x;\n \n let max_x = if partition_x == 0 { i32::MIN } else { nums1[partition_x - 1] };\n let min_x = if partition_x == m { i32::MAX } else { nums1[partition_x] };\n \n let max_y = if partition_y == 0 { i32::MIN } else { nums2[partition_y - 1] };\n let min_y = if partition_y == n { i32::MAX } else { nums2[partition_y] };\n \n if max_x <= min_y && max_y <= min_x {\n if (m + n) % 2 == 0 {\n return (max_x.max(max_y) + min_x.min(min_y)) as f64 / 2.0;\n } else {\n return max_x.max(max_y) as f64;\n }\n } else if max_x > min_y {\n high = partition_x - 1;\n } else {\n low = partition_x + 1;\n }\n }\n \n 0.0\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n if (nums1.size() > nums2.size()) {\n swap(nums1, nums2);\n }\n \n int m = nums1.size();\n int n = nums2.size();\n int low = 0, high = m;\n \n while (low <= high) {\n int partitionX = (low + high) / 2;\n int partitionY = (m + n + 1) / 2 - partitionX;\n \n int maxX = (partitionX == 0) ? INT_MIN : nums1[partitionX - 1];\n int maxY = (partitionY == 0) ? INT_MIN : nums2[partitionY - 1];\n \n int minX = (partitionX == m) ? INT_MAX : nums1[partitionX];\n int minY = (partitionY == n) ? INT_MAX : nums2[partitionY];\n \n if (maxX <= minY && maxY <= minX) {\n if ((m + n) % 2 == 0) {\n return (max(maxX, maxY) + min(minX, minY)) / 2.0;\n } else {\n return max(maxX, maxY);\n }\n } else if (maxX > minY) {\n high = partitionX - 1;\n } else {\n low = partitionX + 1;\n }\n }\n \n throw invalid_argument("Input arrays are not sorted.");\n }\n};\n```\n``` Java []\npublic class Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n if (nums1.length > nums2.length) {\n int[] temp = nums1;\n nums1 = nums2;\n nums2 = temp;\n }\n \n int m = nums1.length;\n int n = nums2.length;\n int low = 0, high = m;\n \n while (low <= high) {\n int partitionX = (low + high) / 2;\n int partitionY = (m + n + 1) / 2 - partitionX;\n \n int maxX = (partitionX == 0) ? Integer.MIN_VALUE : nums1[partitionX - 1];\n int maxY = (partitionY == 0) ? Integer.MIN_VALUE : nums2[partitionY - 1];\n \n int minX = (partitionX == m) ? Integer.MAX_VALUE : nums1[partitionX];\n int minY = (partitionY == n) ? Integer.MAX_VALUE : nums2[partitionY];\n \n if (maxX <= minY && maxY <= minX) {\n if ((m + n) % 2 == 0) {\n return (Math.max(maxX, maxY) + Math.min(minX, minY)) / 2.0;\n } else {\n return Math.max(maxX, maxY);\n }\n } else if (maxX > minY) {\n high = partitionX - 1;\n } else {\n low = partitionX + 1;\n }\n }\n \n throw new IllegalArgumentException("Input arrays are not sorted.");\n }\n}\n```\n``` C# []\npublic class Solution {\n public double FindMedianSortedArrays(int[] nums1, int[] nums2) {\n if (nums1.Length > nums2.Length) {\n int[] temp = nums1;\n nums1 = nums2;\n nums2 = temp;\n }\n \n int m = nums1.Length;\n int n = nums2.Length;\n int low = 0, high = m;\n \n while (low <= high) {\n int partitionX = (low + high) / 2;\n int partitionY = (m + n + 1) / 2 - partitionX;\n \n int maxX = (partitionX == 0) ? int.MinValue : nums1[partitionX - 1];\n int maxY = (partitionY == 0) ? int.MinValue : nums2[partitionY - 1];\n \n int minX = (partitionX == m) ? int.MaxValue : nums1[partitionX];\n int minY = (partitionY == n) ? int.MaxValue : nums2[partitionY];\n \n if (maxX <= minY && maxY <= minX) {\n if ((m + n) % 2 == 0) {\n return (Math.Max(maxX, maxY) + Math.Min(minX, minY)) / 2.0;\n } else {\n return Math.Max(maxX, maxY);\n }\n } else if (maxX > minY) {\n high = partitionX - 1;\n } else {\n low = partitionX + 1;\n }\n }\n \n throw new ArgumentException("Input arrays are not sorted.");\n }\n}\n```\n``` JavaScript []\nvar findMedianSortedArrays = function(nums1, nums2) {\n if (nums1.length > nums2.length) {\n [nums1, nums2] = [nums2, nums1];\n }\n \n const m = nums1.length;\n const n = nums2.length;\n let low = 0, high = m;\n \n while (low <= high) {\n const partitionX = Math.floor((low + high) / 2);\n const partitionY = Math.floor((m + n + 1) / 2) - partitionX;\n \n const maxX = (partitionX === 0) ? Number.MIN_SAFE_INTEGER : nums1[partitionX - 1];\n const maxY = (partitionY === 0) ? Number.MIN_SAFE_INTEGER : nums2[partitionY - 1];\n \n const minX = (partitionX === m) ? Number.MAX_SAFE_INTEGER : nums1[partitionX];\n const minY = (partitionY === n) ? Number.MAX_SAFE_INTEGER : nums2[partitionY];\n \n if (maxX <= minY && maxY <= minX) {\n if ((m + n) % 2 === 0) {\n return (Math.max(maxX, maxY) + Math.min(minX, minY)) / 2;\n } else {\n return Math.max(maxX, maxY);\n }\n } else if (maxX > minY) {\n high = partitionX - 1;\n } else {\n low = partitionX + 1;\n }\n }\n \n throw new Error("Input arrays are not sorted.");\n};\n```\n``` PHP []\nclass Solution {\n function findMedianSortedArrays($nums1, $nums2) {\n if (count($nums1) > count($nums2)) {\n list($nums1, $nums2) = [$nums2, $nums1];\n }\n \n $m = count($nums1);\n $n = count($nums2);\n $low = 0; $high = $m;\n \n while ($low <= $high) {\n $partitionX = intdiv($low + $high, 2);\n $partitionY = intdiv($m + $n + 1, 2) - $partitionX;\n \n $maxX = ($partitionX == 0) ? PHP_INT_MIN : $nums1[$partitionX - 1];\n $maxY = ($partitionY == 0) ? PHP_INT_MIN : $nums2[$partitionY - 1];\n \n $minX = ($partitionX == $m) ? PHP_INT_MAX : $nums1[$partitionX];\n $minY = ($partitionY == $n) ? PHP_INT_MAX : $nums2[$partitionY];\n \n if ($maxX <= $minY && $maxY <= $minX) {\n if (($m + $n) % 2 == 0) {\n return (max($maxX, $maxY) + min($minX, $minY)) / 2.0;\n } else {\n return max($maxX, $maxY);\n }\n } elseif ($maxX > $minY) {\n $high = $partitionX - 1;\n } else {\n $low = $partitionX + 1;\n }\n }\n \n throw new Exception("Input arrays are not sorted.");\n }\n}\n```\n\n## Performance\n\n| Language | Execution Time (ms) | Memory Usage (MB) |\n|-----------|---------------------|--------------------|\n| Rust | 0 | 2 |\n| Java | 1 | 44.5 |\n| Go | 9 | 5.1 |\n| C++ | 16 | 89.6 |\n| PHP | 28 | 18.9 |\n| Python3 | 80 | 16.5 |\n| JavaScript| 85 | 46.6 |\n| Python3 (Two Pointers) | 93 | 16.5 |\n| C# | 98 | 52.1 |\n\n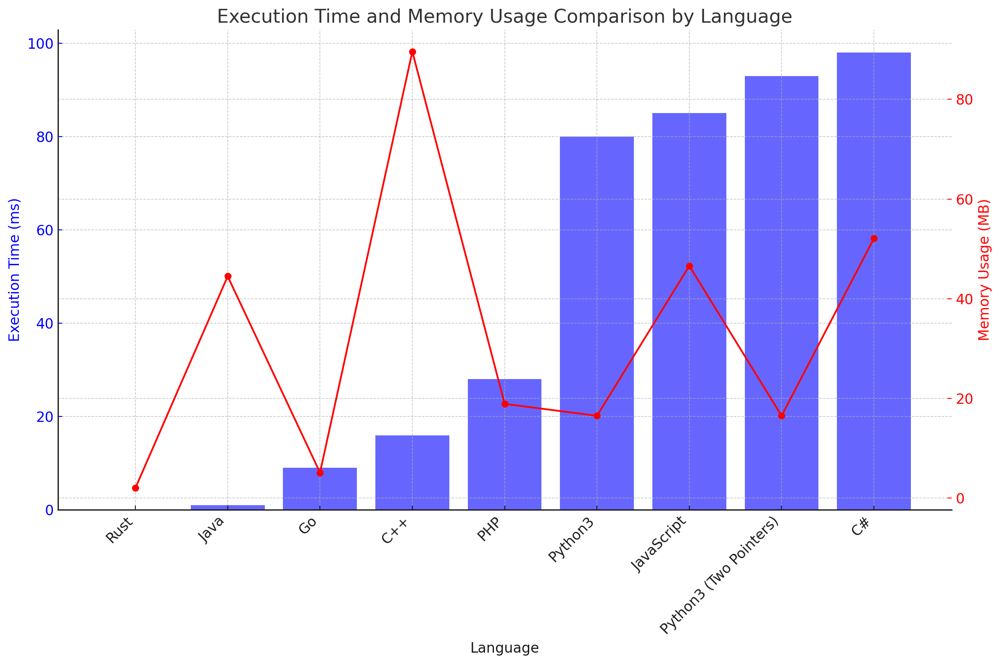\n\n\n## Live Coding in Rust - 0 ms \nhttps://youtu.be/i7qROr8VOuA?si=sjYuouuMThe8BUAM\n\n## Conclusion\n\nBoth strategies have their own unique benefits. While the two-pointers approach offers simplicity and clarity, the binary search approach showcases efficiency and mastery over the properties of sorted arrays. Choosing between them depends on the specific constraints and requirements of a given scenario. | 74 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
🚩📈99.99% Acceptance with Optimised Solution | ✅Explained in Detail🔥 | median-of-two-sorted-arrays | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe median of two sorted arrays is essentially the middle element of the combined sorted array. To find it efficiently, we can use a binary search approach to partition both arrays in such a way that the elements on the left side are smaller or equal to the elements on the right side. By doing this, we ensure that the middle elements of the combined arrays represent the median.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. First, we ensure that nums1 is the smaller of the two arrays by swapping them if necessary. This simplifies the binary search, as we always want to perform it on the smaller array.\n\n2. We define a binary search within the range of left and right for the smaller array (nums1). The initial values of left and right are 0 and the length of nums1, respectively.\n\n3. In each iteration of the binary search, we calculate the partition indices for both nums1 and nums2. These partition indices divide the combined arrays into two halves.\n\n4. We compute the maximum element on the left side and the minimum element on the right side for both partitions.\n\n5. If the maximum element on the left side of the smaller partition (max_left1 or max_left2) is less than or equal to the minimum element on the right side of the larger partition (min_right1 or min_right2), we have found the correct partitioning. We can then calculate the median based on these elements.\n\n6. If the maximum element on the left side of nums1 is greater than the minimum element on the right side of nums2, we adjust the right pointer for nums1 to move left in the binary search. Otherwise, we adjust the left pointer for nums1 to move right.\n\n7. We repeat the binary search until we find the correct partitioning.\n\n8. Finally, we return the median based on the partitioned elements. If the total number of elements is even, we take the average of the two middle elements; otherwise, we return the middle element.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe binary search runs in O(log(min(m, n))) time, where m and n are the lengths of the input arrays nums1 and nums2. This is because we are effectively reducing the search space by half in each iteration.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) because we only use a constant amount of additional space for variables, regardless of the input sizes.\n# Code\n```\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n if (nums1.size() > nums2.size()) {\n swap(nums1, nums2);\n }\n \n int m = nums1.size();\n int n = nums2.size();\n int left = 0, right = m, half_len = (m + n + 1) / 2;\n \n while (left <= right) {\n int partition1 = (left + right) / 2;\n int partition2 = half_len - partition1;\n \n int max_left1 = (partition1 == 0) ? INT_MIN : nums1[partition1 - 1];\n int min_right1 = (partition1 == m) ? INT_MAX : nums1[partition1];\n \n int max_left2 = (partition2 == 0) ? INT_MIN : nums2[partition2 - 1];\n int min_right2 = (partition2 == n) ? INT_MAX : nums2[partition2];\n \n if (max_left1 <= min_right2 && max_left2 <= min_right1) {\n if ((m + n) % 2 == 0) {\n return (max(max_left1, max_left2) + min(min_right1, min_right2)) / 2.0;\n } else {\n return max(max_left1, max_left2);\n }\n } else if (max_left1 > min_right2) {\n right = partition1 - 1;\n } else {\n left = partition1 + 1;\n }\n }\n \n // This should never be reached if the input arrays are sorted correctly.\n throw invalid_argument("Input arrays are not sorted.");\n }\n};\n\n``` | 3 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
My thought process - O(log(min(N, M))) time, O(1) space - Python, JavaScript, Java, C++ | median-of-two-sorted-arrays | 1 | 1 | # Intuition\nWelcome to my article! This starts with `What is median?`. Understanding `median` is a key to solve this quesiton.\n\n---\n\n# Solution Video\n\nToday, I\'m going on business trip. This article is written in a train. lol\nIf I have a time tonight, I will create a solution video for this question.\n\nInstead of the video, I added more comments to the codes.\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,423\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## My thought process - How I think about a solution\n\n### What is `median`?\n\nFirst and foremost, we must understand what `median` is. Without this understanding, we cannot write a program.\n\n`The median is one of the measures of central tendency for data or a set, representing the value that is at the middle position.`\n\n- In the case of an even-sized data set\n\nHowever, in the case of an even-sized data set, the arithmetic mean of the two middle values is taken.\n\nFor example, in a data set consisting of the ages of 6 individuals: `1, 2, 3, 5, 9, 11`, the median is `4 years old` (taking two middle values `3 + 5` and divide by `2`)\n\n- In the case of an odd-sized data set\n\nIn the case of an odd-sized data set, for example, in a data set consisting of the ages of 5 individuals: `10, 32, 96, 100, 105` years old, the median is `96 years old`, which is the value at the 3rd position from both the top and the bottom. If there are 2 more children aged `0`, making a total of 7 individuals `0, 0, 10, 32, 96, 100, 105`, the median becomes `32 years old`.\n\n### My first thought\nNow, I hope you understand what `median` is. Simply, when we convert `median` to program, we can write it like this.\n\nThis is Python code.\n```\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n # Merge the two sorted arrays\n merged = sorted(nums1 + nums2)\n length = len(merged)\n \n # Check if the total length is even or odd\n if length % 2 == 0:\n # If even, return the average of the two middle elements\n return (merged[length // 2 - 1] + merged[length // 2]) / 2\n else:\n # If odd, return the middle element\n return merged[length // 2]\n```\nIt\'s very simple right? In fact, this program passed all cases and execution time is not bad. Beats 68% when I ran the code. If we can use this code for this question. this is acutually easy problem.\n\nThat is my first thought.\n\n### We have a constraint\n\nBut we have a constrant about time complexity. Description says "The overall run time complexity should be `O(log(m+n))`", so we can\'t use my simple solution for this question, even if the simple solution passed all cases.\n\nWe need to find another solution.\n\nLet\'s focus on time complexity of the constraint. Time complexity of `O(log(m+n))` is a constraint, on the other hand, it should be a hint to solve the question. If you know time complexity well, you can guess a solution from `O(log(something))`.\n\nThat is time complexity of `binary search`. That\'s why I stated to focus on a binary search-based solution to find the median of two arrays.\n\nThat is my thoguht process to reach `binary search-based solution`.\n\n---\n\n# Solution\n\n### Algorithm overview:\n1. Ensure that nums1 is the smaller array.\n2. Calculate the lengths of the input arrays nums1 and nums2.\n3. Set the initial range for binary search on nums1 using the variables left and right.\n\n### Detailed Explanation:\n1. Check and swap nums1 and nums2 if nums1 is longer than nums2 to ensure nums1 is the smaller array.\n2. Calculate the lengths of nums1 and nums2 and store them in len1 and len2.\n3. Initialize the binary search range using left (0) and right (length of nums1).\n4. Enter a while loop that continues as long as the left pointer is less than or equal to the right pointer.\n5. Inside the loop:\n a. Calculate the partition points for nums1 and nums2 based on the binary search.\n b. Determine the maximum elements on the left side (max_left) and minimum elements on the right side (min_right) for both arrays.\n c. Check if the current partition is correct by comparing max_left and min_right.\n d. If the partition is correct:\n - If the total length is even, return the average of max_left and min_right.\n - If the total length is odd, return max_left.\n e. If the partition is not correct, adjust the binary search range based on the comparison of max_left1 and min_right2.\n\nThis algorithm efficiently finds the median of two sorted arrays using a binary search approach to adjust the partition points and determine the correct position for the median.\n\n\n---\n\n\n# Complexity\n- Time complexity: O(log(min(N, M)))\nThe while loop performs binary search, and each iteration divides the search range in half. Thus, the time complexity is O(log(min(N, M))), where `N` is the length of nums1 and `M` is the length of nums2.\n\n- Space complexity: O(1)\nThe algorithm uses a constant amount of extra space for variables like `left`, `right`, `partition1`, `partition2`, `max_left1`, `max_left2`, `max_left`, `min_right1`, `min_right2`, and `min_right`. Therefore, the space complexity is O(1), indicating constant space usage irrespective of the input size.\n\n\n```python []\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n # Ensure nums1 is the smaller array\n if len(nums1) > len(nums2):\n nums1, nums2 = nums2, nums1\n \n # Get the lengths of the two arrays\n len1, len2 = len(nums1), len(nums2)\n \n # Set the range for binary search on nums1\n left, right = 0, len1\n \n while left <= right:\n # Partition nums1 and nums2\n partition1 = (left + right) // 2\n partition2 = (len1 + len2 + 1) // 2 - partition1\n \n # Find the maximum elements on the left of the partition\n max_left1 = nums1[partition1-1] if partition1 > 0 else float(\'-inf\')\n max_left2 = nums2[partition2-1] if partition2 > 0 else float(\'-inf\')\n max_left = max(max_left1, max_left2)\n \n # Find the minimum elements on the right of the partition\n min_right1 = nums1[partition1] if partition1 < len1 else float(\'inf\')\n min_right2 = nums2[partition2] if partition2 < len2 else float(\'inf\')\n min_right = min(min_right1, min_right2)\n \n # Check if the partition is correct\n if max_left <= min_right:\n # If the total length is even, return the average of the two middle elements\n if (len1 + len2) % 2 == 0:\n return (max_left + min_right) / 2\n # If the total length is odd, return the middle element\n else:\n return max_left\n elif max_left1 > min_right2:\n right = partition1 - 1\n else:\n left = partition1 + 1\n```\n```javascript []\n/**\n * @param {number[]} nums1\n * @param {number[]} nums2\n * @return {number}\n */\nvar findMedianSortedArrays = function(nums1, nums2) {\n // Ensure nums1 is the smaller array\n if (nums1.length > nums2.length) {\n [nums1, nums2] = [nums2, nums1];\n }\n\n // Get the lengths of the two arrays\n const len1 = nums1.length;\n const len2 = nums2.length;\n\n // Set the range for binary search on nums1\n let left = 0;\n let right = len1;\n\n while (left <= right) {\n // Partition nums1 and nums2\n const partition1 = Math.floor((left + right) / 2);\n const partition2 = Math.floor((len1 + len2 + 1) / 2) - partition1;\n\n // Find the maximum elements on the left of the partition\n const maxLeft1 = partition1 > 0 ? nums1[partition1 - 1] : Number.NEGATIVE_INFINITY;\n const maxLeft2 = partition2 > 0 ? nums2[partition2 - 1] : Number.NEGATIVE_INFINITY;\n const maxLeft = Math.max(maxLeft1, maxLeft2);\n\n // Find the minimum elements on the right of the partition\n const minRight1 = partition1 < len1 ? nums1[partition1] : Number.POSITIVE_INFINITY;\n const minRight2 = partition2 < len2 ? nums2[partition2] : Number.POSITIVE_INFINITY;\n const minRight = Math.min(minRight1, minRight2);\n\n // Check if the partition is correct\n if (maxLeft <= minRight) {\n // If the total length is even, return the average of the two middle elements\n if ((len1 + len2) % 2 === 0) {\n return (maxLeft + minRight) / 2;\n }\n // If the total length is odd, return the middle element\n else {\n return maxLeft;\n }\n } else if (maxLeft1 > minRight2) {\n right = partition1 - 1;\n } else {\n left = partition1 + 1;\n }\n } \n};\n```\n```java []\nclass Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n // Ensure nums1 is the smaller array\n if (nums1.length > nums2.length) {\n int[] temp = nums1;\n nums1 = nums2;\n nums2 = temp;\n }\n\n // Get the lengths of the two arrays\n int len1 = nums1.length;\n int len2 = nums2.length;\n\n // Set the range for binary search on nums1\n int left = 0;\n int right = len1;\n\n while (left <= right) {\n // Partition nums1 and nums2\n int partition1 = (left + right) / 2;\n int partition2 = (len1 + len2 + 1) / 2 - partition1;\n\n // Find the maximum elements on the left of the partition\n int maxLeft1 = partition1 > 0 ? nums1[partition1 - 1] : Integer.MIN_VALUE;\n int maxLeft2 = partition2 > 0 ? nums2[partition2 - 1] : Integer.MIN_VALUE;\n int maxLeft = Math.max(maxLeft1, maxLeft2);\n\n // Find the minimum elements on the right of the partition\n int minRight1 = partition1 < len1 ? nums1[partition1] : Integer.MAX_VALUE;\n int minRight2 = partition2 < len2 ? nums2[partition2] : Integer.MAX_VALUE;\n int minRight = Math.min(minRight1, minRight2);\n\n // Check if the partition is correct\n if (maxLeft <= minRight) {\n // If the total length is even, return the average of the two middle elements\n if ((len1 + len2) % 2 == 0) {\n return (maxLeft + minRight) / 2.0;\n }\n // If the total length is odd, return the middle element\n else {\n return maxLeft;\n }\n } else if (maxLeft1 > minRight2) {\n right = partition1 - 1;\n } else {\n left = partition1 + 1;\n }\n }\n\n return 0.0; // This should not be reached, just to satisfy Java\'s return requirements\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n // Ensure nums1 is the smaller array\n if (nums1.size() > nums2.size()) {\n nums1.swap(nums2);\n }\n\n // Get the lengths of the two arrays\n int len1 = nums1.size();\n int len2 = nums2.size();\n\n // Set the range for binary search on nums1\n int left = 0;\n int right = len1;\n\n while (left <= right) {\n // Partition nums1 and nums2\n int partition1 = (left + right) / 2;\n int partition2 = (len1 + len2 + 1) / 2 - partition1;\n\n // Find the maximum elements on the left of the partition\n int maxLeft1 = partition1 > 0 ? nums1[partition1 - 1] : INT_MIN;\n int maxLeft2 = partition2 > 0 ? nums2[partition2 - 1] : INT_MIN;\n int maxLeft = max(maxLeft1, maxLeft2);\n\n // Find the minimum elements on the right of the partition\n int minRight1 = partition1 < len1 ? nums1[partition1] : INT_MAX;\n int minRight2 = partition2 < len2 ? nums2[partition2] : INT_MAX;\n int minRight = min(minRight1, minRight2);\n\n // Check if the partition is correct\n if (maxLeft <= minRight) {\n // If the total length is even, return the average of the two middle elements\n if ((len1 + len2) % 2 == 0) {\n return (maxLeft + minRight) / 2.0;\n }\n // If the total length is odd, return the middle element\n else {\n return maxLeft;\n }\n } else if (maxLeft1 > minRight2) {\n right = partition1 - 1;\n } else {\n left = partition1 + 1;\n }\n }\n\n return 0.0; // This should not be reached, just to satisfy C++\'s return requirements \n }\n};\n```\n\n---\n\n\nThank you for reading such a long article.\n\n\u2B50\uFE0F If you learn something from the article, please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Sep 22, 2023\nhttps://leetcode.com/problems/is-subsequence/solutions/4074388/video-how-i-think-about-a-solution-ot-time-o1-space-python-javascript-java-c/\n | 34 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
🔥🔥🔥🔥🔥Easy Solution , Simple Method🔥🔥🔥🔥🔥 | median-of-two-sorted-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n merged = sorted(nums1 + nums2)\n length = len(merged)\n\n if length % 2 == 0:\n m, n = length // 2, length // 2 - 1\n return (merged[n] + merged[m]) / 2\n else:\n return merged[length // 2]\n\n``` | 3 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
🚀100% || Two Solutions || Two Pointers & Divide And Conquer || Commented Code🚀 | median-of-two-sorted-arrays | 1 | 1 | # Problem Description\nGiven two sorted arrays, `nums1` and `nums2`, each of sizes `M` and `N` respectively. The **goal** is to find the **median** of the **combined** array formed by merging `nums1` and `nums2`.\n\nThe **task** is to design an algorithm with an overall run time complexity of `O(log(min(m, n)))` to calculate the median of the combined sorted array.\n\n**The median** of an array is the **middle** element when the array is **sorted**. If the combined array has an even number of elements, the median is the **average** of the two middle elements.\n\n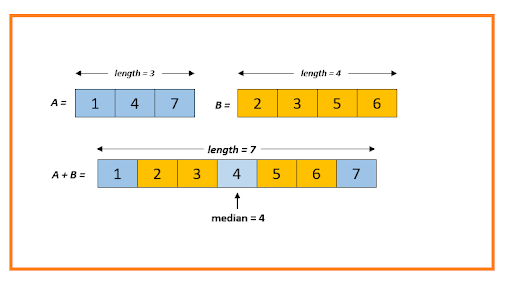\n\n\n\n---\n\n\n# Intuition\nHello There\uD83D\uDE00\nLet\'s take a look on our today\'s interesting problem\uD83D\uDE80\n\nIn our today\'s problem we have, two **sorted** arrays and a **median** to find but the **median** is for the array that **results** from **merging** both of the arrays.\nSounds like a **neat** problem.\uD83E\uDD29\n\n## Two Pointers\nThe **first** solution that would pop in mind is Why don\'t we **merge** the two arrays.\uD83E\uDD14\nWe can do this in **linear** time since the two arrays are **sorted** then we will have `2` pointer each of them on a **different** array from the other and put the **smaller** number in the **available** position in our **new** array.\n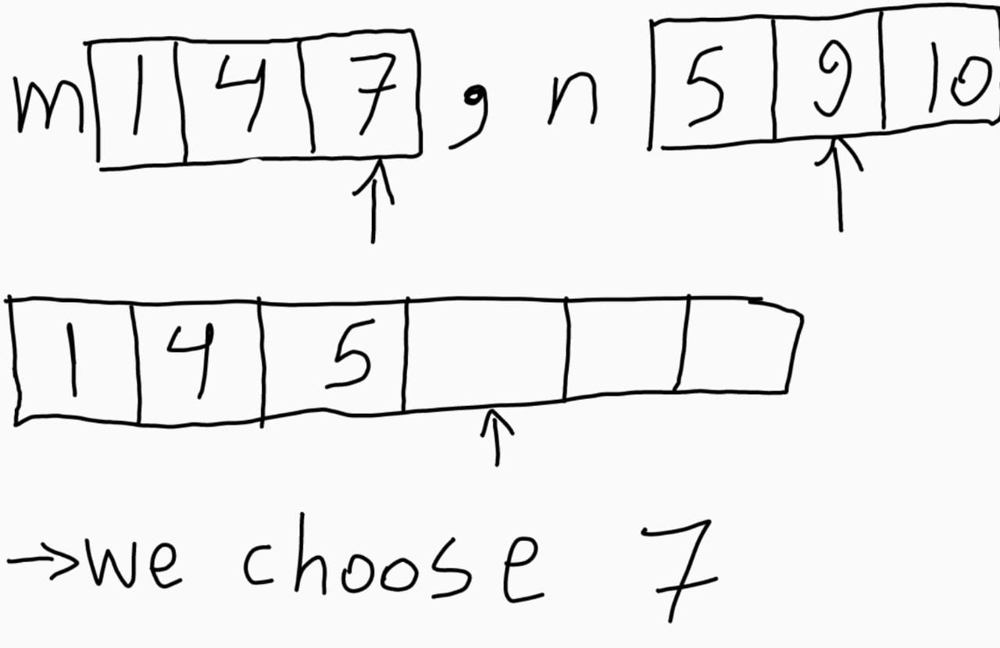\n\nThe **tricky** part here that this solution has **complexity** of `O(m + n)` and still get **accepted** although the problem said it wants an algorithm with `O(log(min(m, n)))`\uD83E\uDD2F\nBut I had `100%` solution in **Java** with **Two Pointers** solution exactly like the next solution that I will discuss.\n\n\n\n## Divide And Conquer\n\n**Divide and Conquer** in a great technique in the world of computer science.\uD83D\uDE80\nIt **shares** something important with **dynamic programming** that both of them **break** the problem into smaller **subproblems**.\nThe **diffrenece** between the two approaches that the subproblems are **independent** in divide and conquer but in dynamic programming there is some **overlapping** between the subproblems.\uD83E\uDD2F\n\n- The **essence** of this solution that two things :\n - **drop** the part of the two arrays that we are sure that our median **won\'t be in it**.\n - **choose** the median when one array has **no elements** in it.\n\nlet\'s look at the **base case**, when we have one array is **empty**\nif you have two arrays `a` , `b` and I told you to get the median of their merge like that:\n```\n-> a = [1, 4, 10]\n-> b = []\n\n-> index median of a + b = 1\n-> median of a + b = 4\n``` \nWe can note here that since `b` is empty then the median is in a with the same **index** we are searching for.\uD83E\uDD2F\n\nLet\'s look at another example:\n```\n-> a = [1, 4, 10]\n-> b = [2, 4, 7, 15]\n-> index median of a + b = 3\n-> mid of a = 1\n-> mid of b = 2\n```\n```\nnew a and b to search in:\n-> a = [1, 4, 10]\n-> b = [2, 4]\n-> index median of a + b = 3\n-> mid of a = 1\n-> mid of b = 1\n```\n```\nnew a and b to search in\n-> a = [10]\n-> b = [2, 4]\n-> index median of a + b = 1\n-> mid of a = 0\n-> mid of b = 1\n```\n```\nnew a and b to search in\n-> a = []\n-> b = [2, 4]\n-> index median of a + b = 1\n```\nWow, we can see now we reached our **base** case that a is **empty** then the solution is the `1` **index** of our new array of b which is `4`.\n\nWe can see in the last example that we applied divide and conquer by **dropping** the **half** of the array that we are sure that our median won\'t be inside it then recursively search in our new arrays until we reach our base case.\uD83D\uDE80\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n# Approach\n## 1. Two Pointers\n1. **Create** a new array `mergedArray` with a size equal to the **sum** of the sizes of `nums1` and `nums2`.\n2. **Initialize** two pointers `idxNums1` and `idxNums2` to `0`, representing the indices for `nums1` and `nums2`.\n3. **Iterate** through mergedArray from `0` to its `size`.\n - **Compare** the elements pointed by `idxNums1` in `nums1` and `idxNums2` in `nums2`.\n - Place the **smaller** element in `mergedArray` and **increment** the respective pointer (`idxNums1` or `idxNums2`).\n4. Check if the **size** of `mergedArray` is **odd** or **even**.\n - If **odd**, return the **middle** element of `mergedArray`.\n - If **even**, return the **average** of the two middle elements in `mergedArray`.\n\n## Complexity\n- **Time complexity:** $$O(N + M)$$ \nSince we are iterating over the big array which has size of `N + M`.\n- **Space complexity:** $$O(N + M)$$\nSince we are storing the new merged array with size of `N + M`.\n\n\n---\n\n## 2. Divide And Conquer\n1. **findKthElement** Function.\n - Handle **base cases** where one of the arrays is **exhausted**.\n - Return the kth element from the remaining array accordingly.\n - **Calculate** mid indices for both arrays to divide and conquer.\n - Based on mid elements, decide which **portion** of the arrays to **discard** and recurse accordingly.\n2. **findMedianSortedArrays** Function.\n - Calculate the **total size** of the merged arrays. \n - If the total size is **odd**, return the kth element where `k = total_size // 2`.\n - If the total size is **even**, find the `kth and (kth - 1)` elements and return their **average**.\n\n## Complexity\n- **Time complexity:** $$O(log(min(M, N)))$$ \nThe **logarithmic** term is because we are using **Divide And Conquer** then each call we divide the size of the two arrays into half.\nThe **minimum** term since the base case is when the size of one of the arrays is `0` and the array which will be faster to reach `0` is the smaller array which is `min(M, N)`\nSo total complexity is `O(log(min(M, N)))` .\n- **Space complexity:** $$O(1)$$\nSince we are only store constant number of variables then complexity is `O(1)`.\n\n\n\n---\n\n\n\n# Code\n## 1. Two Pointers\n```C++ []\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n // Merge the sorted arrays into a single array\n vector<int> mergedArray(nums1.size() + nums2.size());\n \n int idxNums1 = 0; // Index for nums1\n int idxNums2 = 0; // Index for nums2\n \n // Merge the arrays while maintaining the sorted order\n for(int i = 0; i < mergedArray.size(); i++) {\n if (idxNums2 != nums2.size() && (idxNums1 == nums1.size() || nums2[idxNums2] < nums1[idxNums1])) {\n mergedArray[i] = nums2[idxNums2++];\n } else {\n mergedArray[i] = nums1[idxNums1++];\n }\n }\n \n // Calculate the median of the merged array\n if (mergedArray.size() % 2 == 1) {\n return mergedArray[mergedArray.size() / 2];\n } else {\n return ((mergedArray[mergedArray.size() / 2]) + (mergedArray[mergedArray.size() / 2 - 1])) / 2.0;\n }\n }\n};\n```\n```Java []\nclass Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n // Merge the sorted arrays into a single array\n int[] mergedArray = new int[nums1.length + nums2.length];\n\n int idxNums1 = 0; // Index for nums1\n int idxNums2 = 0; // Index for nums2\n\n // Merge the arrays while maintaining the sorted order\n for (int i = 0; i < mergedArray.length; i++) {\n if (idxNums2 < nums2.length && (idxNums1 == nums1.length || nums2[idxNums2] < nums1[idxNums1])) {\n mergedArray[i] = nums2[idxNums2++];\n } else {\n mergedArray[i] = nums1[idxNums1++];\n }\n }\n\n // Calculate the median of the merged array\n if (mergedArray.length % 2 == 1) {\n return mergedArray[mergedArray.length / 2];\n } else {\n return (mergedArray[mergedArray.length / 2] + mergedArray[mergedArray.length / 2 - 1]) / 2.0;\n }\n }\n}\n```\n```Python []\nclass Solution:\n def findMedianSortedArrays(self, nums1, nums2) -> float:\n merged_array = [0] * (len(nums1) + len(nums2))\n idx_nums1 = 0 # Index for nums1\n idx_nums2 = 0 # Index for nums2\n\n # Merge the arrays while maintaining the sorted order\n for i in range(len(merged_array)):\n if idx_nums2 < len(nums2) and (idx_nums1 == len(nums1) or nums2[idx_nums2] < nums1[idx_nums1]):\n merged_array[i] = nums2[idx_nums2]\n idx_nums2 += 1\n else:\n merged_array[i] = nums1[idx_nums1]\n idx_nums1 += 1\n\n # Calculate the median of the merged array\n if len(merged_array) % 2 == 1:\n return merged_array[len(merged_array) // 2]\n else:\n return (merged_array[len(merged_array) // 2] + merged_array[len(merged_array) // 2 - 1]) / 2.0\n```\n\n## 2. Divide And Conquer\n```C++ []\nclass Solution {\npublic:\n // Helper function to find the kth element in merged sorted arrays\n double findKthElement(int k, vector<int>& nums1, vector<int>& nums2, int start1, int end1, int start2, int end2) {\n // Base cases when one array is exhausted\n if (start1 >= end1)\n return nums2[start2 + k];\n if (start2 >= end2)\n return nums1[start1 + k];\n\n // Calculate mid indices\n int mid1 = (end1 - start1) / 2;\n int mid2 = (end2 - start2) / 2;\n\n // Compare mid elements and recurse accordingly\n if (mid1 + mid2 < k) {\n if (nums1[start1 + mid1] > nums2[start2 + mid2])\n // Discard elements before mid2 and search in the remaining array\n return findKthElement(k - mid2 - 1, nums1, nums2, start1, end1, start2 + mid2 + 1, end2);\n else\n // Discard elements before mid1 and search in the remaining array\n return findKthElement(k - mid1 - 1, nums1, nums2, start1 + mid1 + 1, end1, start2, end2);\n } else {\n if (nums1[start1 + mid1] > nums2[start2 + mid2])\n // Discard elements after mid1 and search in the remaining array\n return findKthElement(k, nums1, nums2, start1, start1 + mid1, start2, end2);\n else\n // Discard elements after mid2 and search in the remaining array\n return findKthElement(k, nums1, nums2, start1, end1, start2, start2 + mid2);\n }\n }\n\n // Function to find the median of merged sorted arrays\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n int size1 = nums1.size();\n int size2 = nums2.size();\n int totalSize = size1 + size2;\n\n // Check if the total size is odd or even and find the median accordingly\n if (totalSize % 2 == 1)\n // For odd total size, median is the kth element where k = total_size // 2\n return findKthElement(totalSize / 2, nums1, nums2, 0, size1, 0, size2);\n else {\n // For even total size, median is the average of kth and (kth - 1) elements\n int num1 = findKthElement(totalSize / 2, nums1, nums2, 0, size1, 0, size2);\n int num2 = findKthElement(totalSize / 2 - 1, nums1, nums2, 0, size1, 0, size2);\n\n return (num1 + num2) / 2.0;\n }\n }\n};\n```\n```Java []\nclass Solution {\n // Helper function to find the kth element in merged sorted arrays\n private double findKthElement(int k, int[] nums1, int[] nums2, int start1, int end1, int start2, int end2) {\n // Base cases when one array is exhausted\n if (start1 >= end1)\n return nums2[start2 + k];\n if (start2 >= end2)\n return nums1[start1 + k];\n\n // Calculate mid indices\n int mid1 = (end1 - start1) / 2;\n int mid2 = (end2 - start2) / 2;\n\n // Compare mid elements and recurse accordingly\n if (mid1 + mid2 < k) {\n if (nums1[start1 + mid1] > nums2[start2 + mid2])\n // Discard elements before mid2 and search in the remaining array\n return findKthElement(k - mid2 - 1, nums1, nums2, start1, end1, start2 + mid2 + 1, end2);\n else\n // Discard elements before mid1 and search in the remaining array\n return findKthElement(k - mid1 - 1, nums1, nums2, start1 + mid1 + 1, end1, start2, end2);\n } else {\n if (nums1[start1 + mid1] > nums2[start2 + mid2])\n // Discard elements after mid1 and search in the remaining array\n return findKthElement(k, nums1, nums2, start1, start1 + mid1, start2, end2);\n else\n // Discard elements after mid2 and search in the remaining array\n return findKthElement(k, nums1, nums2, start1, end1, start2, start2 + mid2);\n }\n }\n\n // Function to find the median of merged sorted arrays\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n int size1 = nums1.length;\n int size2 = nums2.length;\n int totalSize = size1 + size2;\n\n // Check if the total size is odd or even and find the median accordingly\n if (totalSize % 2 == 1)\n // For odd total size, median is the kth element where k = total_size // 2\n return findKthElement(totalSize / 2, nums1, nums2, 0, size1, 0, size2);\n else {\n // For even total size, median is the average of kth and (kth - 1) elements\n double num1 = findKthElement(totalSize / 2, nums1, nums2, 0, size1, 0, size2);\n double num2 = findKthElement(totalSize / 2 - 1, nums1, nums2, 0, size1, 0, size2);\n\n return (num1 + num2) / 2.0;\n }\n }\n}\n```\n```Python []\nclass Solution:\n def find_kth_element(self, k, nums1, nums2):\n # Base cases when one array is exhausted\n if not nums1:\n return nums2[k]\n if not nums2:\n return nums1[k]\n\n mid1 = len(nums1) // 2 # Midpoint of nums1\n mid2 = len(nums2) // 2 # Midpoint of nums2\n\n if mid1 + mid2 < k:\n if nums1[mid1] > nums2[mid2]:\n # Discard elements before mid2 and search in the remaining array\n return self.find_kth_element(k - mid2 - 1, nums1, nums2[mid2 + 1:])\n else:\n # Discard elements before mid1 and search in the remaining array\n return self.find_kth_element(k - mid1 - 1, nums1[mid1 + 1:], nums2)\n else:\n if nums1[mid1] > nums2[mid2]:\n # Discard elements after mid1 and search in the remaining array\n return self.find_kth_element(k, nums1[:mid1], nums2)\n else:\n # Discard elements after mid2 and search in the remaining array\n return self.find_kth_element(k, nums1, nums2[:mid2])\n\n def findMedianSortedArrays(self, nums1, nums2):\n total_size = len(nums1) + len(nums2)\n\n if total_size % 2 == 1:\n # For odd total size, median is the kth element where k = total_size // 2\n return self.find_kth_element(total_size // 2, nums1, nums2)\n else:\n # For even total size, median is the average of kth and (kth - 1) elements\n k1 = total_size // 2\n k2 = total_size // 2 - 1\n num1 = self.find_kth_element(k1, nums1, nums2)\n num2 = self.find_kth_element(k2, nums1, nums2)\n return (num1 + num2) / 2.0\n```\n\n \n\n\n | 22 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
✅Mastering Finding Median in Sorted Arrays 💡 Beginner's Guide | median-of-two-sorted-arrays | 1 | 1 | # \u2753 Finding Median in Sorted Arrays \u2753\n\n## \uD83D\uDCA1Approach 1: Brute Force\n\n### \u2728Explanation\nThe brute force approach involves merging two sorted arrays into a single array and then calculating the median based on the length of the merged array. This method has a time complexity of O((N + M) * log(N + M)), where N and M are the lengths of the input arrays.\n\n### \uD83D\uDCDDDry Run\n1. Merge `nums1` and `nums2` into a new array `sortedArr`.\n2. Sort `sortedArr`.\n3. If the total length is even, return the average of the middle two elements; otherwise, return the middle element.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: O((N + M) * log(N + M))\n- Space Complexity: O(N + M)\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n// C++ code block for the brute force approach\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n // Merge two arrays\n vector<int> mergedArr(nums1.begin(), nums1.end());\n mergedArr.insert(mergedArr.end(), nums2.begin(), nums2.end());\n\n // Sort the merged array\n sort(mergedArr.begin(), mergedArr.end());\n\n // Calculate median based on the length\n int n = mergedArr.size();\n if (n % 2 == 0) {\n return (double)(mergedArr[n / 2 - 1] + mergedArr[n / 2]) / 2.0;\n } else {\n return (double)mergedArr[n / 2];\n }\n }\n};\n```\n\n```java []\n// Java code block for the brute force approach\nclass Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n // Merge two arrays\n int[] mergedArr = new int[nums1.length + nums2.length];\n System.arraycopy(nums1, 0, mergedArr, 0, nums1.length);\n System.arraycopy(nums2, 0, mergedArr, nums1.length, nums2.length);\n\n // Sort the merged array\n Arrays.sort(mergedArr);\n\n // Calculate median based on the length\n int n = mergedArr.length;\n if (n % 2 == 0) {\n return (double) (mergedArr[n / 2 - 1] + mergedArr[n / 2]) / 2.0;\n } else {\n return (double) mergedArr[n / 2];\n }\n }\n}\n```\n\n```python []\n# Python code block for the brute force approach\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n # Merge two arrays\n merged_arr = nums1 + nums2\n\n # Sort the merged array\n merged_arr.sort()\n\n # Calculate median based on the length\n n = len(merged_arr)\n if n % 2 == 0:\n return (merged_arr[n // 2 - 1] + merged_arr[n // 2]) / 2.0\n else:\n return float(merged_arr[n // 2])\n```\n\n```csharp []\n// C# code block for the brute force approach\npublic class Solution {\n public double FindMedianSortedArrays(int[] nums1, int[] nums2) {\n // Merge two arrays\n int[] mergedArr = new int[nums1.Length + nums2.Length];\n Array.Copy(nums1, 0, mergedArr, 0, nums1.Length);\n Array.Copy(nums2, 0, mergedArr, nums1.Length, nums2.Length);\n\n // Sort the merged array\n Array.Sort(mergedArr);\n\n // Calculate median based on the length\n int n = mergedArr.Length;\n if (n % 2 == 0) {\n return (double)(mergedArr[n / 2 - 1] + mergedArr[n / 2]) / 2.0;\n } else {\n return (double)mergedArr[n / 2];\n }\n }\n}\n```\n\n```javascript []\n// JavaScript code block for the brute force approach\nclass Solution {\n findMedianSortedArrays(nums1, nums2) {\n // Merge two arrays\n const mergedArr = [...nums1, ...nums2];\n\n // Sort the merged array\n mergedArr.sort((a, b) => a - b);\n\n // Calculate median based on the length\n const n = mergedArr.length;\n if (n % 2 === 0) {\n return (mergedArr[n / 2 - 1] + mergedArr[n / 2]) / 2.0;\n } else {\n return mergedArr[Math.floor(n / 2)];\n }\n }\n}\n```\n---\n\n## \uD83D\uDCA1Approach 2: Merge Sorted Arrays\n\n### \u2728Explanation\nThe second approach involves merging two sorted arrays in a single pass. This is achieved by comparing elements from both arrays and inserting the smaller one into a new array. The time complexity is O(N + M), where N and M are the lengths of the input arrays.\n\n### \uD83D\uDCDDDry Run\n1. Initialize two pointers (`i` and `j`) for `nums1` and `nums2` respectively.\n2. Compare elements at `i` and `j`.\n3. Insert the smaller element into the new array `a`.\n4. Move the pointer for the array with the smaller element.\n5. Repeat until both arrays are exhausted.\n6. If the total length is even, return the average of the middle two elements; otherwise, return the middle element.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: O(N + M)\n- Space Complexity: O(N + M)\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n// C++ code block for the merge sorted arrays approach\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0;\n vector<int> a;\n\n while (i < nums1.size() && j < nums2.size()) {\n if (nums1[i] < nums2[j]) {\n a.push_back(nums1[i]);\n i++;\n } else {\n a.push_back(nums2[j]);\n j++;\n }\n }\n\n for (; i < nums1.size(); i++) {\n a.push_back(nums1[i]);\n }\n\n for (; j < nums2.size(); j++) {\n a.push_back(nums2[j]);\n }\n\n int n = a.size();\n if (n % 2 == 0) {\n return (double)(a[n / 2 - 1] + a[n / 2]) / 2.0;\n } else {\n return (double)a[n / 2];\n }\n }\n};\n```\n\n```java []\n// Java code block for the merge sorted arrays approach\nclass\n\n Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n int i = 0, j = 0;\n List<Integer> a = new ArrayList<>();\n\n while (i < nums1.length && j < nums2.length) {\n if (nums1[i] < nums2[j]) {\n a.add(nums1[i]);\n i++;\n } else {\n a.add(nums2[j]);\n j++;\n }\n }\n\n while (i < nums1.length) {\n a.add(nums1[i]);\n i++;\n }\n\n while (j < nums2.length) {\n a.add(nums2[j]);\n j++;\n }\n\n int n = a.size();\n if (n % 2 == 0) {\n return (double)(a.get(n / 2 - 1) + a.get(n / 2)) / 2.0;\n } else {\n return (double)a.get(n / 2);\n }\n }\n}\n```\n\n```python []\n# Python code block for the merge sorted arrays approach\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n i, j = 0, 0\n a = []\n\n while i < len(nums1) and j < len(nums2):\n if nums1[i] < nums2[j]:\n a.append(nums1[i])\n i += 1\n else:\n a.append(nums2[j])\n j += 1\n\n a.extend(nums1[i:])\n a.extend(nums2[j:])\n\n n = len(a)\n if n % 2 == 0:\n return (a[n // 2 - 1] + a[n // 2]) / 2.0\n else:\n return float(a[n // 2])\n```\n\n```csharp []\n// C# code block for the merge sorted arrays approach\npublic class Solution {\n public double FindMedianSortedArrays(int[] nums1, int[] nums2) {\n int i = 0, j = 0;\n List<int> a = new List<int>();\n\n while (i < nums1.Length && j < nums2.Length) {\n if (nums1[i] < nums2[j]) {\n a.Add(nums1[i]);\n i++;\n } else {\n a.Add(nums2[j]);\n j++;\n }\n }\n\n while (i < nums1.Length) {\n a.Add(nums1[i]);\n i++;\n }\n\n while (j < nums2.Length) {\n a.Add(nums2[j]);\n j++;\n }\n\n int n = a.Count;\n if (n % 2 == 0) {\n return (double)(a[n / 2 - 1] + a[n / 2]) / 2.0;\n } else {\n return (double)a[n / 2];\n }\n }\n}\n```\n\n```javascript []\n// JavaScript code block for the merge sorted arrays approach\nclass Solution {\n findMedianSortedArrays(nums1, nums2) {\n let i = 0, j = 0;\n const a = [];\n\n while (i < nums1.length && j < nums2.length) {\n if (nums1[i] < nums2[j]) {\n a.push(nums1[i]);\n i++;\n } else {\n a.push(nums2[j]);\n j++;\n }\n }\n\n while (i < nums1.length) {\n a.push(nums1[i]);\n i++;\n }\n\n while (j < nums2.length) {\n a.push(nums2[j]);\n j++;\n }\n\n const n = a.length;\n if (n % 2 === 0) {\n return (a[n / 2 - 1] + a[n / 2]) / 2.0;\n } else {\n return a[Math.floor(n / 2)];\n }\n }\n}\n```\n---\n\n## \uD83D\uDCA1Approach 3: Binary Search\n\n### \u2728Explanation\nThe binary search approach involves partitioning both arrays such that the elements on the left side are smaller than the elements on the right side. The median is found when the partitioning satisfies certain conditions. This method has a time complexity of O(log(min(N, M))), where N and M are the lengths of the input arrays.\n\n### \uD83D\uDCDDDry Run\n1. Initialize two pointers (`low` and `high`) for the smaller array (`nums1` or `nums2`).\n2. Perform binary search to find the correct partition such that elements on the left side are smaller than elements on the right side.\n3. Adjust the pointers based on the comparison of elements.\n4. Calculate the median based on the partition.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- Time Complexity: O(log(min(N, M)))\n- Space Complexity: O(1)\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\n// C++ code block for the binary search approach\nclass Solution {\npublic:\n double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {\n // Ensure nums1 is the smaller array\n if (nums1.size() > nums2.size()) {\n swap(nums1, nums2);\n }\n\n int x = nums1.size();\n int y = nums2.size();\n int low = 0, high = x;\n\n while (low <= high) {\n int partitionX = (low + high) / 2;\n int partitionY = (x + y + 1) / 2 - partitionX;\n\n int maxX = (partitionX == 0) ? INT_MIN : nums1[partitionX - 1];\n int minX = (partitionX == x) ? INT_MAX : nums1[partitionX];\n\n int maxY = (partitionY == 0) ? INT_MIN : nums2[partitionY - 1];\n int minY = (partitionY == y) ? INT_MAX : nums2[partitionY];\n\n if (maxX <= minY && maxY <= minX) {\n if ((x + y) % 2 == 0) {\n return (double)(max(maxX, maxY) + min(minX, minY)) / 2.0;\n } else {\n return (double)max(maxX, maxY);\n }\n } else if (maxX > minY) {\n high = partitionX - 1;\n } else {\n low = partitionX + 1;\n }\n }\n\n throw invalid_argument("Input arrays are not sorted!");\n }\n};\n```\n\n```java []\n// Java code block for the binary search approach\nclass Solution {\n public double findMedianSortedArrays(int[] nums1, int[] nums2) {\n // Ensure nums1 is the smaller array\n if (nums1.length > nums2.length) {\n int[] temp = nums1;\n nums1 = nums2;\n nums2 = temp;\n }\n\n int x = nums1.length;\n int y = nums2.length;\n int low = 0, high = x;\n\n while (low <= high) {\n int partitionX = (low + high) / 2;\n int partitionY = (x + y + 1) / 2 - partitionX;\n\n int maxX = (partitionX == 0) ? Integer.MIN_VALUE : nums1[partitionX - 1];\n int minX = (partitionX == x) ? Integer.MAX_VALUE : nums1[partitionX];\n\n int maxY = (partitionY == 0) ? Integer.MIN_VALUE : nums2[partitionY - 1];\n int minY = (partitionY == y) ? Integer.MAX_VALUE : nums2[partitionY];\n\n if (maxX <= minY && maxY <= minX) {\n if ((x + y) % 2 == 0) {\n return (double) (Math.max(maxX, maxY) + Math.min(minX, minY)) / 2.0;\n } else {\n return (double) Math.max(maxX, maxY);\n }\n } else if (maxX > minY) {\n high = partitionX - 1;\n } else {\n low = partitionX + 1;\n }\n }\n\n throw new IllegalArgumentException("Input arrays are not sorted!");\n }\n}\n```\n\n```python []\n# Python code block for the binary search approach\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n # Ensure nums1 is the smaller array\n if len(nums1) > len(nums2):\n nums1, nums2 = nums2, nums1\n\n x, y = len(nums1), len(nums2)\n low, high = 0, x\n\n while low <= high:\n partitionX = (low + high) // 2\n partitionY = (x + y + 1) // 2 - partitionX\n\n maxX = float(\'-inf\') if partitionX == 0 else nums1[partitionX - 1]\n minX = float(\'inf\') if partitionX == x else nums1[partitionX]\n\n maxY = float(\'-inf\') if partitionY == 0 else nums2[partitionY - 1]\n minY = float(\'inf\') if partitionY == y else nums2[partitionY]\n\n if maxX <= minY and maxY <= minX:\n if (x + y) % 2 == 0:\n return (max(maxX, maxY) + min(minX, minY)) / 2.0\n else:\n return float(max(maxX, maxY))\n elif maxX > minY:\n high = partitionX - 1\n else:\n low = partitionX + 1\n\n raise ValueError("Input arrays are not sorted!")\n```\n\n```csharp []\n// C# code block for the binary search approach\npublic class Solution {\n public double FindMedianSortedArrays(int[] nums1, int[] nums2) {\n // Ensure nums1 is the smaller array\n if (nums1.Length > nums2.Length) {\n int[] temp = nums1;\n nums1 = nums2;\n nums2 = temp;\n }\n\n int x = nums1.Length;\n int y = nums2.Length;\n int low = 0, high = x;\n\n while (low <= high) {\n int partitionX = (low + high) / 2;\n int partitionY = (x + y + 1) / 2 - partitionX;\n\n int maxX = (partitionX == 0) ? int.MinValue : nums1[partitionX - 1];\n int minX = (partitionX == x) ? int.MaxValue : nums1[partitionX];\n\n int maxY = (partitionY == 0) ? int.MinValue : nums2[partitionY - 1];\n int minY = (partitionY == y) ? int.MaxValue : nums2[partitionY];\n\n if (maxX <= minY && maxY <= minX) {\n if ((x + y) % 2 == 0) {\n return (double)(Math.Max(maxX, maxY) + Math.Min(minX, minY)) / 2.0;\n } else {\n return (double)Math.Max(maxX, maxY);\n }\n } else if (maxX > minY) {\n high = partitionX - 1;\n } else {\n low = partitionX + 1;\n }\n }\n\n throw new ArgumentException("Input arrays are not sorted!");\n }\n}\n```\n\n```javascript []\n// JavaScript code block for the binary search approach\nclass Solution {\n findMedianSortedArrays(nums1, nums2) {\n // Ensure nums1 is the smaller array\n if (nums1.length > nums2.length) {\n [nums1, nums2] = [nums2, nums1];\n }\n\n const x = nums1.length;\n const y = nums2.length;\n let low = 0;\n let high = x;\n\n while (low <= high) {\n const partitionX = Math.floor((low + high) / 2);\n const partitionY = Math.floor((x + y + 1) / 2) - partitionX;\n\n const maxX = (partitionX === 0) ? Number.MIN_SAFE_INTEGER : nums1[partitionX - 1];\n const minX = (partitionX === x) ? Number.MAX_SAFE_INTEGER : nums1[partitionX];\n\n const maxY = (partitionY === 0) ? Number.MIN_SAFE_INTEGER : nums2[partitionY - 1];\n const minY = (partitionY === y) ? Number.MAX_SAFE_INTEGER : nums2[partitionY];\n\n if (maxX <= minY && maxY <= minX) {\n if ((x + y) % 2 === 0) {\n return (Math.max(maxX, maxY) + Math.min(minX, minY)) / 2.0;\n } else {\n return Math.max(maxX, maxY);\n }\n } else if (maxX > minY) {\n high = partitionX - 1;\n } else {\n low = partitionX + 1;\n }\n }\n\n throw new Error("Input arrays are not sorted!");\n }\n}\n```\n---\n# Don\'t Forget UPVOTING\u2B06\uFE0F\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *LB AKA MR.ROBOT SIGNING OFF*\n\n | 2 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
median of two sorted arrays | median-of-two-sorted-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n num=[]\n if len(nums1)==0 and len(nums2)==0:\n return 0\n if len(nums1)>0:\n for i in (nums1):\n num.append(i)\n if len(nums2)>0:\n for j in (nums2):\n num.append(j)\n num.sort()\n p=len(num)\n if(p%2!=0):\n a=(p)//2\n median=num[a]\n elif p==1:\n median=num[0]\n elif p==2:\n median=(num[0]+num[1])/2\n else:\n z=(p//2)-1\n b=p//2\n median=(num[z]+num[b])/2\n return median\n``` | 0 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
Find the Median of Sorted List || Python || Easy Solution || Beats 90.40 % | median-of-two-sorted-arrays | 0 | 1 | \n# Algorithm\n<!-- Describe your approach to solving the problem. -->\n1. Merge the given lists.\n````\nnums1.extend(nums2)\n````\n2. Now sort the merged list.\n````\nnums1.sort()\n````\n3. Find the middle element of the sorted list.\n```\nmid = len(nums1)//2\n```\n4. If the length of the sorted list is even : \n```\nif len(nums1)%2 == 0:\n return (nums1[mid-1]+nums1[mid])/2\n```\n5. If the length of the sorted list is odd : \n```\nelse:\n return nums1[mid]\n```\n\n---\n\nIf you find my solution helpful, Do give it an upvote. It would be encouraging.\n\n# Code\n```\nclass Solution:\n def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:\n nums1.extend(nums2)\n nums1.sort()\n mid = len(nums1)//2\n if len(nums1)%2 == 0:\n return (nums1[mid-1]+nums1[mid])/2\n else:\n return nums1[mid]\n\n``` | 2 | Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
The overall run time complexity should be `O(log (m+n))`.
**Example 1:**
**Input:** nums1 = \[1,3\], nums2 = \[2\]
**Output:** 2.00000
**Explanation:** merged array = \[1,2,3\] and median is 2.
**Example 2:**
**Input:** nums1 = \[1,2\], nums2 = \[3,4\]
**Output:** 2.50000
**Explanation:** merged array = \[1,2,3,4\] and median is (2 + 3) / 2 = 2.5.
**Constraints:**
* `nums1.length == m`
* `nums2.length == n`
* `0 <= m <= 1000`
* `0 <= n <= 1000`
* `1 <= m + n <= 2000`
* `-106 <= nums1[i], nums2[i] <= 106` | null |
✅ Beats 96.49% 🔥 || 5 Different Approaches 💡 || Brute Force || EAC || DP || MA || Recursion || | longest-palindromic-substring | 1 | 1 | ### It takes a lot of efforts to write such long explanatinon, so please UpVote \u2B06\uFE0F if this helps you.\n\n# Approach 1: Brute Force\n\n\n\n# Intuition :\n\n**The obvious brute force solution is to pick all possible starting and ending positions for a substring, and verify if it is a palindrome. There are a total of n^2 such substrings (excluding the trivial solution where a character itself is a palindrome). Since verifying each substring takes O(n) time, the run time complexity is O(n^3).**\n\n# Algorithm :\n1. Pick a starting index for the current substring which is every index from 0 to n-2.\n2. Now, pick the ending index for the current substring which is every index from i+1 to n-1.\n3. Check if the substring from ith index to jth index is a palindrome.\n4. If step 3 is true and length of substring is greater than maximum length so far, update maximum length and maximum substring. \n5. Print the maximum substring.\n\n# Complexity Analysis\n- Time complexity : ***O(n^3)***. Assume that n is the length of the input string, there are a total of C(n, 2) = n(n-1)/2 substrings (excluding the trivial solution where a character itself is a palindrome). Since verifying each substring takes O(n) time, the run time complexity is O(n^3).\n\n- Space complexity : ***O(1)***.\n\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) <= 1:\n return s\n \n Max_Len=1\n Max_Str=s[0]\n for i in range(len(s)-1):\n for j in range(i+1,len(s)):\n if j-i+1 > Max_Len and s[i:j+1] == s[i:j+1][::-1]:\n Max_Len = j-i+1\n Max_Str = s[i:j+1]\n\n return Max_Str\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n if (s.length() <= 1) {\n return s;\n }\n \n int max_len = 1;\n std::string max_str = s.substr(0, 1);\n \n for (int i = 0; i < s.length(); ++i) {\n for (int j = i + max_len; j <= s.length(); ++j) {\n if (j - i > max_len && isPalindrome(s.substr(i, j - i))) {\n max_len = j - i;\n max_str = s.substr(i, j - i);\n }\n }\n }\n\n return max_str;\n }\n\nprivate:\n bool isPalindrome(const std::string& str) {\n int left = 0;\n int right = str.length() - 1;\n \n while (left < right) {\n if (str[left] != str[right]) {\n return false;\n }\n ++left;\n --right;\n }\n \n return true;\n }\n};\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.length() <= 1) {\n return s;\n }\n\n int maxLen = 1;\n String maxStr = s.substring(0, 1);\n\n for (int i = 0; i < s.length(); i++) {\n for (int j = i + maxLen; j <= s.length(); j++) {\n if (j - i > maxLen && isPalindrome(s.substring(i, j))) {\n maxLen = j - i;\n maxStr = s.substring(i, j);\n }\n }\n }\n\n return maxStr;\n }\n\n private boolean isPalindrome(String str) {\n int left = 0;\n int right = str.length() - 1;\n\n while (left < right) {\n if (str.charAt(left) != str.charAt(right)) {\n return false;\n }\n left++;\n right--;\n }\n\n return true;\n }\n}\n```\n# Approach 2: Expand Around Center\n\n\n# Intuition :\n\n**To enumerate all palindromic substrings of a given string, we first expand a given string at each possible starting position of a palindrome and also at each possible ending position of a palindrome and keep track of the length of the longest palindrome we found so far.**\n\n# Approach :\n1. We observe that a palindrome mirrors around its center. Therefore, a palindrome can be expanded from its center, and there are only 2n - 1 such centers.\n2. You might be asking why there are 2n - 1 but not n centers? The reason is the center of a palindrome can be in between two letters. Such palindromes have even number of letters (such as "abba") and its center are between the two \'b\'s.\'\n3. Since expanding a palindrome around its center could take O(n) time, the overall complexity is O(n^2).\n\n# Algorithm :\n1. At starting we have maz_str = s[0] and max_len = 1 as every single character is a palindrome.\n2. Now, we will iterate over the string and for every character we will expand around its center.\n3. For odd length palindrome, we will consider the current character as the center and expand around it.\n4. For even length palindrome, we will consider the current character and the next character as the center and expand around it.\n5. We will keep track of the maximum length and the maximum substring.\n6. Print the maximum substring.\n\n# Complexity Analysis\n- Time complexity : ***O(n^2)***. Since expanding a palindrome around its center could take O(n) time, the overall complexity is O(n^2).\n\n- Space complexity : ***O(1)***.\n\n# Code\n\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) <= 1:\n return s\n\n def expand_from_center(left, right):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return s[left + 1:right]\n\n max_str = s[0]\n\n for i in range(len(s) - 1):\n odd = expand_from_center(i, i)\n even = expand_from_center(i, i + 1)\n\n if len(odd) > len(max_str):\n max_str = odd\n if len(even) > len(max_str):\n max_str = even\n\n return max_str\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n if (s.length() <= 1) {\n return s;\n }\n\n auto expand_from_center = [&](int left, int right) {\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n return s.substr(left + 1, right - left - 1);\n };\n\n std::string max_str = s.substr(0, 1);\n\n for (int i = 0; i < s.length() - 1; i++) {\n std::string odd = expand_from_center(i, i);\n std::string even = expand_from_center(i, i + 1);\n\n if (odd.length() > max_str.length()) {\n max_str = odd;\n }\n if (even.length() > max_str.length()) {\n max_str = even;\n }\n }\n\n return max_str;\n }\n};\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.length() <= 1) {\n return s;\n }\n\n String maxStr = s.substring(0, 1);\n\n for (int i = 0; i < s.length() - 1; i++) {\n String odd = expandFromCenter(s, i, i);\n String even = expandFromCenter(s, i, i + 1);\n\n if (odd.length() > maxStr.length()) {\n maxStr = odd;\n }\n if (even.length() > maxStr.length()) {\n maxStr = even;\n }\n }\n\n return maxStr;\n }\n\n private String expandFromCenter(String s, int left, int right) {\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n left--;\n right++;\n }\n return s.substring(left + 1, right);\n }\n}\n\n```\n# Approach 3: Dynamic Programming\n\n\n\n# Intuition :\n\n\n**To improve over the brute force solution, we first observe how we can avoid unnecessary re-computation while validating palindromes. Consider the case "ababa". If we already knew that "bab" is a palindrome, it is obvious that "ababa" must be a palindrome since the two left and right end letters are the same.**\n\n# Algorithm :\n1. We initialize a boolean table dp and mark all the values as false.\n2. We will use a variable max_len to keep track of the maximum length of the palindrome.\n3. We will iterate over the string and mark the diagonal elements as true as every single character is a palindrome.\n4. Now, we will iterate over the string and for every character we will expand around its center.\n5. For odd length palindrome, we will consider the current character as the center and expand around it.\n6. For even length palindrome, we will consider the current character and the next character as the center and expand around it.\n7. We will keep track of the maximum length and the maximum substring.\n8. Print the maximum substring.\n\n# Complexity Analysis\n- Time complexity : ***O(n^2)***. This gives us a runtime complexity of O(n^2).\n\n- Space complexity : ***O(n^2)***. It uses O(n^2) space to store the table.\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) <= 1:\n return s\n \n Max_Len=1\n Max_Str=s[0]\n dp = [[False for _ in range(len(s))] for _ in range(len(s))]\n for i in range(len(s)):\n dp[i][i] = True\n for j in range(i):\n if s[j] == s[i] and (i-j <= 2 or dp[j+1][i-1]):\n dp[j][i] = True\n if i-j+1 > Max_Len:\n Max_Len = i-j+1\n Max_Str = s[j:i+1]\n return Max_Str\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n if (s.length() <= 1) {\n return s;\n }\n \n int max_len = 1;\n int start = 0;\n int end = 0;\n std::vector<std::vector<bool>> dp(s.length(), std::vector<bool>(s.length(), false));\n \n for (int i = 0; i < s.length(); ++i) {\n dp[i][i] = true;\n for (int j = 0; j < i; ++j) {\n if (s[j] == s[i] && (i - j <= 2 || dp[j + 1][i - 1])) {\n dp[j][i] = true;\n if (i - j + 1 > max_len) {\n max_len = i - j + 1;\n start = j;\n end = i;\n }\n }\n }\n }\n \n return s.substr(start, end - start + 1);\n }\n};\n\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.length() <= 1) {\n return s;\n }\n\n int maxLen = 1;\n int start = 0;\n int end = 0;\n boolean[][] dp = new boolean[s.length()][s.length()];\n\n for (int i = 0; i < s.length(); ++i) {\n dp[i][i] = true;\n for (int j = 0; j < i; ++j) {\n if (s.charAt(j) == s.charAt(i) && (i - j <= 2 || dp[j + 1][i - 1])) {\n dp[j][i] = true;\n if (i - j + 1 > maxLen) {\n maxLen = i - j + 1;\n start = j;\n end = i;\n }\n }\n }\n }\n\n return s.substring(start, end + 1);\n }\n}\n\n```\n\n# Approach 4: Manacher\'s Algorithm\n\n\n# Intuition :\n\n**To avoid the unnecessary validation of palindromes, we can use Manacher\'s algorithm. The algorithm is explained brilliantly in this article. The idea is to use palindrome property to avoid unnecessary validations. We maintain a center and right boundary of a palindrome. We use previously calculated values to determine if we can expand around the center or not. If we can expand, we expand and update the center and right boundary. Otherwise, we move to the next character and repeat the process. We also maintain a variable max_len to keep track of the maximum length of the palindrome. We also maintain a variable max_str to keep track of the maximum substring.**\n\n# Algorithm :\n1. We initialize a boolean table dp and mark all the values as false.\n2. We will use a variable max_len to keep track of the maximum length of the palindrome.\n3. We will iterate over the string and mark the diagonal elements as true as every single character is a palindrome.\n4. Now, we will iterate over the string and for every character we will expand around its center.\n5. For odd length palindrome, we will consider the current character as the center and expand around it.\n6. For even length palindrome, we will consider the current character and the next character as the center and expand around it.\n7. We will keep track of the maximum length and the maximum substring.\n8. Print the maximum substring.\n\n# Complexity Analysis\n- Time complexity : ***O(n)***. Since expanding a palindrome around its center could take O(n) time, the overall complexity is O(n).\n\n- Space complexity : ***O(n)***. It uses O(n) space to store the table.\n\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) <= 1:\n return s\n \n Max_Len=1\n Max_Str=s[0]\n s = \'#\' + \'#\'.join(s) + \'#\'\n dp = [0 for _ in range(len(s))]\n center = 0\n right = 0\n for i in range(len(s)):\n if i < right:\n dp[i] = min(right-i, dp[2*center-i])\n while i-dp[i]-1 >= 0 and i+dp[i]+1 < len(s) and s[i-dp[i]-1] == s[i+dp[i]+1]:\n dp[i] += 1\n if i+dp[i] > right:\n center = i\n right = i+dp[i]\n if dp[i] > Max_Len:\n Max_Len = dp[i]\n Max_Str = s[i-dp[i]:i+dp[i]+1].replace(\'#\',\'\')\n return Max_Str\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n if (s.length() <= 1) {\n return s;\n }\n \n int maxLen = 1;\n std::string maxStr = s.substr(0, 1);\n s = "#" + std::regex_replace(s, std::regex(""), "#") + "#";\n std::vector<int> dp(s.length(), 0);\n int center = 0;\n int right = 0;\n \n for (int i = 0; i < s.length(); ++i) {\n if (i < right) {\n dp[i] = std::min(right - i, dp[2 * center - i]);\n }\n \n while (i - dp[i] - 1 >= 0 && i + dp[i] + 1 < s.length() && s[i - dp[i] - 1] == s[i + dp[i] + 1]) {\n dp[i]++;\n }\n \n if (i + dp[i] > right) {\n center = i;\n right = i + dp[i];\n }\n \n if (dp[i] > maxLen) {\n maxLen = dp[i];\n maxStr = s.substr(i - dp[i], 2 * dp[i] + 1);\n maxStr.erase(std::remove(maxStr.begin(), maxStr.end(), \'#\'), maxStr.end());\n }\n }\n \n return maxStr;\n }\n};\n\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.length() <= 1) {\n return s;\n }\n\n int maxLen = 1;\n String maxStr = s.substring(0, 1);\n s = "#" + s.replaceAll("", "#") + "#";\n int[] dp = new int[s.length()];\n int center = 0;\n int right = 0;\n\n for (int i = 0; i < s.length(); i++) {\n if (i < right) {\n dp[i] = Math.min(right - i, dp[2 * center - i]);\n }\n\n while (i - dp[i] - 1 >= 0 && i + dp[i] + 1 < s.length() && s.charAt(i - dp[i] - 1) == s.charAt(i + dp[i] + 1)) {\n dp[i]++;\n }\n\n if (i + dp[i] > right) {\n center = i;\n right = i + dp[i];\n }\n\n if (dp[i] > maxLen) {\n maxLen = dp[i];\n maxStr = s.substring(i - dp[i], i + dp[i] + 1).replaceAll("#", "");\n }\n }\n\n return maxStr;\n }\n}\n```\n\n# Approach 5: Recursive TLE(Time Limit Exceeded)\n\n# Intuition :\n\n**The obvious brute force solution is to pick all possible starting and ending positions for a substring, and verify if it is a palindrome. There are a total of n^2 such substrings (excluding the trivial solution where a character itself is a palindrome). Since verifying each substring takes O(n) time, the run time complexity is O(n^3). But in this approach we will use recursion to solve the problem. We will check if the string is a palindrome or not. If it is a palindrome, we will return the string. Otherwise, we will recursively call the function for the string excluding the first character and for the string excluding the last character. We will check the length of the returned strings and return the string with the maximum length.**\n\n# Algorithm :\n1. If the string is a palindrome, we will return the string.\n2. Otherwise, we will recursively call the function for the string excluding the first character and for the string excluding the last character.\n3. We will check the length of the returned strings and return the string with the maximum length.\n\n# Complexity Analysis \n- Time complexity : ***O(n^3)***. Assume that n is the length of the input string, there are a total of C(n, 2) = n(n-1)/2 substrings (excluding the trivial solution where a character itself is a palindrome). Since verifying each substring takes O(n) time, the run time complexity is O(n^3).\n\n- Space complexity : ***O(n)***. The recursion stack may go up to n levels deep.\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n\n if s==s[::-1]: \n return s\n left = self.longestPalindrome(s[1:])\n right = self.longestPalindrome(s[:-1])\n\n if len(left)>len(right):\n return left\n else:\n return right\n```\n``` C++ []\nclass Solution {\npublic:\n string longestPalindrome(string s) {\n if (s == string(s.rbegin(), s.rend())) {\n return s;\n }\n\n string left = longestPalindrome(s.substr(1));\n string right = longestPalindrome(s.substr(0, s.size() - 1));\n\n if (left.length() > right.length()) {\n return left;\n } else {\n return right;\n }\n }\n};\n\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.equals(new StringBuilder(s).reverse().toString())) {\n return s;\n }\n\n String left = longestPalindrome(s.substring(1));\n String right = longestPalindrome(s.substring(0, s.length() - 1));\n\n if (left.length() > right.length()) {\n return left;\n } else {\n return right;\n }\n }\n}\n```\n\n\n | 350 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅ Beats 96.49% 🔥 || 5 Different Approaches 💡 || Brute Force || EAC || DP || MA || Recursion || | longest-palindromic-substring | 1 | 1 | ### It takes a lot of efforts to write such long explanatinon, so please UpVote \u2B06\uFE0F if this helps you.\n\n# Approach 1: Brute Force\n\n\n\n# Intuition :\n\n**The obvious brute force solution is to pick all possible starting and ending positions for a substring, and verify if it is a palindrome. There are a total of n^2 such substrings (excluding the trivial solution where a character itself is a palindrome). Since verifying each substring takes O(n) time, the run time complexity is O(n^3).**\n\n# Algorithm :\n1. Pick a starting index for the current substring which is every index from 0 to n-2.\n2. Now, pick the ending index for the current substring which is every index from i+1 to n-1.\n3. Check if the substring from ith index to jth index is a palindrome.\n4. If step 3 is true and length of substring is greater than maximum length so far, update maximum length and maximum substring. \n5. Print the maximum substring.\n\n# Complexity Analysis\n- Time complexity : ***O(n^3)***. Assume that n is the length of the input string, there are a total of C(n, 2) = n(n-1)/2 substrings (excluding the trivial solution where a character itself is a palindrome). Since verifying each substring takes O(n) time, the run time complexity is O(n^3).\n\n- Space complexity : ***O(1)***.\n\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) <= 1:\n return s\n \n Max_Len=1\n Max_Str=s[0]\n for i in range(len(s)-1):\n for j in range(i+1,len(s)):\n if j-i+1 > Max_Len and s[i:j+1] == s[i:j+1][::-1]:\n Max_Len = j-i+1\n Max_Str = s[i:j+1]\n\n return Max_Str\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n if (s.length() <= 1) {\n return s;\n }\n \n int max_len = 1;\n std::string max_str = s.substr(0, 1);\n \n for (int i = 0; i < s.length(); ++i) {\n for (int j = i + max_len; j <= s.length(); ++j) {\n if (j - i > max_len && isPalindrome(s.substr(i, j - i))) {\n max_len = j - i;\n max_str = s.substr(i, j - i);\n }\n }\n }\n\n return max_str;\n }\n\nprivate:\n bool isPalindrome(const std::string& str) {\n int left = 0;\n int right = str.length() - 1;\n \n while (left < right) {\n if (str[left] != str[right]) {\n return false;\n }\n ++left;\n --right;\n }\n \n return true;\n }\n};\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.length() <= 1) {\n return s;\n }\n\n int maxLen = 1;\n String maxStr = s.substring(0, 1);\n\n for (int i = 0; i < s.length(); i++) {\n for (int j = i + maxLen; j <= s.length(); j++) {\n if (j - i > maxLen && isPalindrome(s.substring(i, j))) {\n maxLen = j - i;\n maxStr = s.substring(i, j);\n }\n }\n }\n\n return maxStr;\n }\n\n private boolean isPalindrome(String str) {\n int left = 0;\n int right = str.length() - 1;\n\n while (left < right) {\n if (str.charAt(left) != str.charAt(right)) {\n return false;\n }\n left++;\n right--;\n }\n\n return true;\n }\n}\n```\n# Approach 2: Expand Around Center\n\n\n# Intuition :\n\n**To enumerate all palindromic substrings of a given string, we first expand a given string at each possible starting position of a palindrome and also at each possible ending position of a palindrome and keep track of the length of the longest palindrome we found so far.**\n\n# Approach :\n1. We observe that a palindrome mirrors around its center. Therefore, a palindrome can be expanded from its center, and there are only 2n - 1 such centers.\n2. You might be asking why there are 2n - 1 but not n centers? The reason is the center of a palindrome can be in between two letters. Such palindromes have even number of letters (such as "abba") and its center are between the two \'b\'s.\'\n3. Since expanding a palindrome around its center could take O(n) time, the overall complexity is O(n^2).\n\n# Algorithm :\n1. At starting we have maz_str = s[0] and max_len = 1 as every single character is a palindrome.\n2. Now, we will iterate over the string and for every character we will expand around its center.\n3. For odd length palindrome, we will consider the current character as the center and expand around it.\n4. For even length palindrome, we will consider the current character and the next character as the center and expand around it.\n5. We will keep track of the maximum length and the maximum substring.\n6. Print the maximum substring.\n\n# Complexity Analysis\n- Time complexity : ***O(n^2)***. Since expanding a palindrome around its center could take O(n) time, the overall complexity is O(n^2).\n\n- Space complexity : ***O(1)***.\n\n# Code\n\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) <= 1:\n return s\n\n def expand_from_center(left, right):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return s[left + 1:right]\n\n max_str = s[0]\n\n for i in range(len(s) - 1):\n odd = expand_from_center(i, i)\n even = expand_from_center(i, i + 1)\n\n if len(odd) > len(max_str):\n max_str = odd\n if len(even) > len(max_str):\n max_str = even\n\n return max_str\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n if (s.length() <= 1) {\n return s;\n }\n\n auto expand_from_center = [&](int left, int right) {\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n return s.substr(left + 1, right - left - 1);\n };\n\n std::string max_str = s.substr(0, 1);\n\n for (int i = 0; i < s.length() - 1; i++) {\n std::string odd = expand_from_center(i, i);\n std::string even = expand_from_center(i, i + 1);\n\n if (odd.length() > max_str.length()) {\n max_str = odd;\n }\n if (even.length() > max_str.length()) {\n max_str = even;\n }\n }\n\n return max_str;\n }\n};\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.length() <= 1) {\n return s;\n }\n\n String maxStr = s.substring(0, 1);\n\n for (int i = 0; i < s.length() - 1; i++) {\n String odd = expandFromCenter(s, i, i);\n String even = expandFromCenter(s, i, i + 1);\n\n if (odd.length() > maxStr.length()) {\n maxStr = odd;\n }\n if (even.length() > maxStr.length()) {\n maxStr = even;\n }\n }\n\n return maxStr;\n }\n\n private String expandFromCenter(String s, int left, int right) {\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n left--;\n right++;\n }\n return s.substring(left + 1, right);\n }\n}\n\n```\n# Approach 3: Dynamic Programming\n\n\n\n# Intuition :\n\n\n**To improve over the brute force solution, we first observe how we can avoid unnecessary re-computation while validating palindromes. Consider the case "ababa". If we already knew that "bab" is a palindrome, it is obvious that "ababa" must be a palindrome since the two left and right end letters are the same.**\n\n# Algorithm :\n1. We initialize a boolean table dp and mark all the values as false.\n2. We will use a variable max_len to keep track of the maximum length of the palindrome.\n3. We will iterate over the string and mark the diagonal elements as true as every single character is a palindrome.\n4. Now, we will iterate over the string and for every character we will expand around its center.\n5. For odd length palindrome, we will consider the current character as the center and expand around it.\n6. For even length palindrome, we will consider the current character and the next character as the center and expand around it.\n7. We will keep track of the maximum length and the maximum substring.\n8. Print the maximum substring.\n\n# Complexity Analysis\n- Time complexity : ***O(n^2)***. This gives us a runtime complexity of O(n^2).\n\n- Space complexity : ***O(n^2)***. It uses O(n^2) space to store the table.\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) <= 1:\n return s\n \n Max_Len=1\n Max_Str=s[0]\n dp = [[False for _ in range(len(s))] for _ in range(len(s))]\n for i in range(len(s)):\n dp[i][i] = True\n for j in range(i):\n if s[j] == s[i] and (i-j <= 2 or dp[j+1][i-1]):\n dp[j][i] = True\n if i-j+1 > Max_Len:\n Max_Len = i-j+1\n Max_Str = s[j:i+1]\n return Max_Str\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n if (s.length() <= 1) {\n return s;\n }\n \n int max_len = 1;\n int start = 0;\n int end = 0;\n std::vector<std::vector<bool>> dp(s.length(), std::vector<bool>(s.length(), false));\n \n for (int i = 0; i < s.length(); ++i) {\n dp[i][i] = true;\n for (int j = 0; j < i; ++j) {\n if (s[j] == s[i] && (i - j <= 2 || dp[j + 1][i - 1])) {\n dp[j][i] = true;\n if (i - j + 1 > max_len) {\n max_len = i - j + 1;\n start = j;\n end = i;\n }\n }\n }\n }\n \n return s.substr(start, end - start + 1);\n }\n};\n\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.length() <= 1) {\n return s;\n }\n\n int maxLen = 1;\n int start = 0;\n int end = 0;\n boolean[][] dp = new boolean[s.length()][s.length()];\n\n for (int i = 0; i < s.length(); ++i) {\n dp[i][i] = true;\n for (int j = 0; j < i; ++j) {\n if (s.charAt(j) == s.charAt(i) && (i - j <= 2 || dp[j + 1][i - 1])) {\n dp[j][i] = true;\n if (i - j + 1 > maxLen) {\n maxLen = i - j + 1;\n start = j;\n end = i;\n }\n }\n }\n }\n\n return s.substring(start, end + 1);\n }\n}\n\n```\n\n# Approach 4: Manacher\'s Algorithm\n\n\n# Intuition :\n\n**To avoid the unnecessary validation of palindromes, we can use Manacher\'s algorithm. The algorithm is explained brilliantly in this article. The idea is to use palindrome property to avoid unnecessary validations. We maintain a center and right boundary of a palindrome. We use previously calculated values to determine if we can expand around the center or not. If we can expand, we expand and update the center and right boundary. Otherwise, we move to the next character and repeat the process. We also maintain a variable max_len to keep track of the maximum length of the palindrome. We also maintain a variable max_str to keep track of the maximum substring.**\n\n# Algorithm :\n1. We initialize a boolean table dp and mark all the values as false.\n2. We will use a variable max_len to keep track of the maximum length of the palindrome.\n3. We will iterate over the string and mark the diagonal elements as true as every single character is a palindrome.\n4. Now, we will iterate over the string and for every character we will expand around its center.\n5. For odd length palindrome, we will consider the current character as the center and expand around it.\n6. For even length palindrome, we will consider the current character and the next character as the center and expand around it.\n7. We will keep track of the maximum length and the maximum substring.\n8. Print the maximum substring.\n\n# Complexity Analysis\n- Time complexity : ***O(n)***. Since expanding a palindrome around its center could take O(n) time, the overall complexity is O(n).\n\n- Space complexity : ***O(n)***. It uses O(n) space to store the table.\n\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) <= 1:\n return s\n \n Max_Len=1\n Max_Str=s[0]\n s = \'#\' + \'#\'.join(s) + \'#\'\n dp = [0 for _ in range(len(s))]\n center = 0\n right = 0\n for i in range(len(s)):\n if i < right:\n dp[i] = min(right-i, dp[2*center-i])\n while i-dp[i]-1 >= 0 and i+dp[i]+1 < len(s) and s[i-dp[i]-1] == s[i+dp[i]+1]:\n dp[i] += 1\n if i+dp[i] > right:\n center = i\n right = i+dp[i]\n if dp[i] > Max_Len:\n Max_Len = dp[i]\n Max_Str = s[i-dp[i]:i+dp[i]+1].replace(\'#\',\'\')\n return Max_Str\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n if (s.length() <= 1) {\n return s;\n }\n \n int maxLen = 1;\n std::string maxStr = s.substr(0, 1);\n s = "#" + std::regex_replace(s, std::regex(""), "#") + "#";\n std::vector<int> dp(s.length(), 0);\n int center = 0;\n int right = 0;\n \n for (int i = 0; i < s.length(); ++i) {\n if (i < right) {\n dp[i] = std::min(right - i, dp[2 * center - i]);\n }\n \n while (i - dp[i] - 1 >= 0 && i + dp[i] + 1 < s.length() && s[i - dp[i] - 1] == s[i + dp[i] + 1]) {\n dp[i]++;\n }\n \n if (i + dp[i] > right) {\n center = i;\n right = i + dp[i];\n }\n \n if (dp[i] > maxLen) {\n maxLen = dp[i];\n maxStr = s.substr(i - dp[i], 2 * dp[i] + 1);\n maxStr.erase(std::remove(maxStr.begin(), maxStr.end(), \'#\'), maxStr.end());\n }\n }\n \n return maxStr;\n }\n};\n\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.length() <= 1) {\n return s;\n }\n\n int maxLen = 1;\n String maxStr = s.substring(0, 1);\n s = "#" + s.replaceAll("", "#") + "#";\n int[] dp = new int[s.length()];\n int center = 0;\n int right = 0;\n\n for (int i = 0; i < s.length(); i++) {\n if (i < right) {\n dp[i] = Math.min(right - i, dp[2 * center - i]);\n }\n\n while (i - dp[i] - 1 >= 0 && i + dp[i] + 1 < s.length() && s.charAt(i - dp[i] - 1) == s.charAt(i + dp[i] + 1)) {\n dp[i]++;\n }\n\n if (i + dp[i] > right) {\n center = i;\n right = i + dp[i];\n }\n\n if (dp[i] > maxLen) {\n maxLen = dp[i];\n maxStr = s.substring(i - dp[i], i + dp[i] + 1).replaceAll("#", "");\n }\n }\n\n return maxStr;\n }\n}\n```\n\n# Approach 5: Recursive TLE(Time Limit Exceeded)\n\n# Intuition :\n\n**The obvious brute force solution is to pick all possible starting and ending positions for a substring, and verify if it is a palindrome. There are a total of n^2 such substrings (excluding the trivial solution where a character itself is a palindrome). Since verifying each substring takes O(n) time, the run time complexity is O(n^3). But in this approach we will use recursion to solve the problem. We will check if the string is a palindrome or not. If it is a palindrome, we will return the string. Otherwise, we will recursively call the function for the string excluding the first character and for the string excluding the last character. We will check the length of the returned strings and return the string with the maximum length.**\n\n# Algorithm :\n1. If the string is a palindrome, we will return the string.\n2. Otherwise, we will recursively call the function for the string excluding the first character and for the string excluding the last character.\n3. We will check the length of the returned strings and return the string with the maximum length.\n\n# Complexity Analysis \n- Time complexity : ***O(n^3)***. Assume that n is the length of the input string, there are a total of C(n, 2) = n(n-1)/2 substrings (excluding the trivial solution where a character itself is a palindrome). Since verifying each substring takes O(n) time, the run time complexity is O(n^3).\n\n- Space complexity : ***O(n)***. The recursion stack may go up to n levels deep.\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n\n if s==s[::-1]: \n return s\n left = self.longestPalindrome(s[1:])\n right = self.longestPalindrome(s[:-1])\n\n if len(left)>len(right):\n return left\n else:\n return right\n```\n``` C++ []\nclass Solution {\npublic:\n string longestPalindrome(string s) {\n if (s == string(s.rbegin(), s.rend())) {\n return s;\n }\n\n string left = longestPalindrome(s.substr(1));\n string right = longestPalindrome(s.substr(0, s.size() - 1));\n\n if (left.length() > right.length()) {\n return left;\n } else {\n return right;\n }\n }\n};\n\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n if (s.equals(new StringBuilder(s).reverse().toString())) {\n return s;\n }\n\n String left = longestPalindrome(s.substring(1));\n String right = longestPalindrome(s.substring(0, s.length() - 1));\n\n if (left.length() > right.length()) {\n return left;\n } else {\n return right;\n }\n }\n}\n```\n\n\n | 350 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
🔥 Easy solution | JAVA | Python 3 🔥| Manacher's algorithm | | longest-palindromic-substring | 1 | 1 | # Intuition\nUsing Manacher\'s algorithm to find the longest palindromic substring efficiently. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. String Transformation: The input string \'s\' is transformed into a new string \'modified_s\' by inserting special characters (\'#\') between each character and at the beginning and end. This transformation allows the algorithm to handle both even and odd-length palindromes in the same way.\n\n1. Initialization: Initialize variables to keep track of the current center \'C\' and the right boundary \'R\' of the current palindrome. Also, initialize variables to store the maximum length of a palindrome found (\'max_len\') and its center (\'max_center\').\n\n1. Palindromic Length Array: Create an array \'P\' to store the length of palindromes at each position in the \'modified_s\' string. Initialize it with zeros.\n\n1. Loop through the String: Iterate through the characters of \'modified_s\'. For each character \'modified_s[i]\', do the following:\n\n 1. If \'i\' is within the right boundary \'R\', calculate the mirror position \'mirror\' of \'i\' with respect to the center \'C\'. Update \'P[i]\' as the minimum of the remaining length of the current palindrome (\'R - i\') and the corresponding value in \'P[mirror]\'. This step takes advantage of known palindromes to avoid redundant computations.\n 1. Expand around \'i\': Check if the characters at positions \'a\' and \'b\' are the same, where \'a\' is the position one character to the right and \'b\' is one character to the left of \'i\'. While the characters at \'a\' and \'b\' match and are within the bounds of the string, increment \'P[i]\' and move \'a\' and \'b\' outwards.\n 1. Update the center and right boundary: If \'i + P[i]\' exceeds the right boundary \'R\', update \'C\' and \'R\' to \'i\' and \'i + P[i]\' to represent the new center and right boundary of the current palindrome.\n 1. Update the maximum length: If \'P[i]\' is greater than \'max_len\', update \'max_len\' and \'max_center\' to \'P[i]\' and \'i\', respectively.\n1. Find the Longest Palindromic Substring: After the loop, calculate the start and end indices of the longest palindromic substring by using the \'max_len\' and \'max_center\'. The start index is calculated as (max_center - max_len) // 2, and the end index is \'start + max_len\'.\n\n1. Return the Result: Return the longest palindromic substring by extracting the substring from \'s\' using the start and end indices.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n modified_s = "#"\n for char in s:\n modified_s += char + "#"\n\n n = len(modified_s)\n P = [0] * n # Array to store the length of palindromes at each position\n C, R = 0, 0 # Center and right boundary of the current palindrome\n\n max_len = 0 # Maximum length of a palindrome found\n max_center = 0 # Center of the palindrome with maximum length\n\n for i in range(n):\n if i < R:\n mirror = 2 * C - i # Mirror position of i\n P[i] = min(R - i, P[mirror])\n\n # Expand around the current character\n a, b = i + (1 + P[i]), i - (1 + P[i])\n while a < n and b >= 0 and modified_s[a] == modified_s[b]:\n P[i] += 1\n a += 1\n b -= 1\n\n # Update the center and right boundary if needed\n if i + P[i] > R:\n C, R = i, i + P[i]\n\n # Update the maximum length and its center\n if P[i] > max_len:\n max_len = P[i]\n max_center = i\n\n start = (max_center - max_len) // 2 # Start index of the longest palindrome\n end = start + max_len # End index of the longest palindrome\n\n return s[start:end]\n \n```\n```java []\nclass Solution {\n public String longestPalindrome(String s) {\n if (s == null || s.length() < 1) return "";\n\n // Transform the input string to include special characters\n StringBuilder modifiedS = new StringBuilder("#");\n for (char c : s.toCharArray()) {\n modifiedS.append(c).append("#");\n }\n\n int n = modifiedS.length();\n int[] P = new int[n]; // Array to store the length of palindromes at each position\n int C = 0; // Center of the current palindrome\n int R = 0; // Right boundary of the current palindrome\n\n int maxLen = 0; // Maximum length of a palindrome found\n int maxCenter = 0; // Center of the palindrome with maximum length\n\n for (int i = 0; i < n; i++) {\n if (i < R) {\n int mirror = 2 * C - i; // Mirror position of i\n P[i] = Math.min(R - i, P[mirror]);\n }\n\n // Expand around the current character\n int a = i + (1 + P[i]);\n int b = i - (1 + P[i]);\n while (a < n && b >= 0 && modifiedS.charAt(a) == modifiedS.charAt(b)) {\n P[i]++;\n a++;\n b--;\n }\n\n // Update the center and right boundary if needed\n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n\n // Update the maximum length and its center\n if (P[i] > maxLen) {\n maxLen = P[i];\n maxCenter = i;\n }\n }\n\n int start = (maxCenter - maxLen) / 2; // Start index of the longest palindrome\n int end = start + maxLen; // End index of the longest palindrome\n\n return s.substring(start, end);\n }\n}\n```\n\n | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
🔥 Easy solution | JAVA | Python 3 🔥| Manacher's algorithm | | longest-palindromic-substring | 1 | 1 | # Intuition\nUsing Manacher\'s algorithm to find the longest palindromic substring efficiently. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. String Transformation: The input string \'s\' is transformed into a new string \'modified_s\' by inserting special characters (\'#\') between each character and at the beginning and end. This transformation allows the algorithm to handle both even and odd-length palindromes in the same way.\n\n1. Initialization: Initialize variables to keep track of the current center \'C\' and the right boundary \'R\' of the current palindrome. Also, initialize variables to store the maximum length of a palindrome found (\'max_len\') and its center (\'max_center\').\n\n1. Palindromic Length Array: Create an array \'P\' to store the length of palindromes at each position in the \'modified_s\' string. Initialize it with zeros.\n\n1. Loop through the String: Iterate through the characters of \'modified_s\'. For each character \'modified_s[i]\', do the following:\n\n 1. If \'i\' is within the right boundary \'R\', calculate the mirror position \'mirror\' of \'i\' with respect to the center \'C\'. Update \'P[i]\' as the minimum of the remaining length of the current palindrome (\'R - i\') and the corresponding value in \'P[mirror]\'. This step takes advantage of known palindromes to avoid redundant computations.\n 1. Expand around \'i\': Check if the characters at positions \'a\' and \'b\' are the same, where \'a\' is the position one character to the right and \'b\' is one character to the left of \'i\'. While the characters at \'a\' and \'b\' match and are within the bounds of the string, increment \'P[i]\' and move \'a\' and \'b\' outwards.\n 1. Update the center and right boundary: If \'i + P[i]\' exceeds the right boundary \'R\', update \'C\' and \'R\' to \'i\' and \'i + P[i]\' to represent the new center and right boundary of the current palindrome.\n 1. Update the maximum length: If \'P[i]\' is greater than \'max_len\', update \'max_len\' and \'max_center\' to \'P[i]\' and \'i\', respectively.\n1. Find the Longest Palindromic Substring: After the loop, calculate the start and end indices of the longest palindromic substring by using the \'max_len\' and \'max_center\'. The start index is calculated as (max_center - max_len) // 2, and the end index is \'start + max_len\'.\n\n1. Return the Result: Return the longest palindromic substring by extracting the substring from \'s\' using the start and end indices.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n modified_s = "#"\n for char in s:\n modified_s += char + "#"\n\n n = len(modified_s)\n P = [0] * n # Array to store the length of palindromes at each position\n C, R = 0, 0 # Center and right boundary of the current palindrome\n\n max_len = 0 # Maximum length of a palindrome found\n max_center = 0 # Center of the palindrome with maximum length\n\n for i in range(n):\n if i < R:\n mirror = 2 * C - i # Mirror position of i\n P[i] = min(R - i, P[mirror])\n\n # Expand around the current character\n a, b = i + (1 + P[i]), i - (1 + P[i])\n while a < n and b >= 0 and modified_s[a] == modified_s[b]:\n P[i] += 1\n a += 1\n b -= 1\n\n # Update the center and right boundary if needed\n if i + P[i] > R:\n C, R = i, i + P[i]\n\n # Update the maximum length and its center\n if P[i] > max_len:\n max_len = P[i]\n max_center = i\n\n start = (max_center - max_len) // 2 # Start index of the longest palindrome\n end = start + max_len # End index of the longest palindrome\n\n return s[start:end]\n \n```\n```java []\nclass Solution {\n public String longestPalindrome(String s) {\n if (s == null || s.length() < 1) return "";\n\n // Transform the input string to include special characters\n StringBuilder modifiedS = new StringBuilder("#");\n for (char c : s.toCharArray()) {\n modifiedS.append(c).append("#");\n }\n\n int n = modifiedS.length();\n int[] P = new int[n]; // Array to store the length of palindromes at each position\n int C = 0; // Center of the current palindrome\n int R = 0; // Right boundary of the current palindrome\n\n int maxLen = 0; // Maximum length of a palindrome found\n int maxCenter = 0; // Center of the palindrome with maximum length\n\n for (int i = 0; i < n; i++) {\n if (i < R) {\n int mirror = 2 * C - i; // Mirror position of i\n P[i] = Math.min(R - i, P[mirror]);\n }\n\n // Expand around the current character\n int a = i + (1 + P[i]);\n int b = i - (1 + P[i]);\n while (a < n && b >= 0 && modifiedS.charAt(a) == modifiedS.charAt(b)) {\n P[i]++;\n a++;\n b--;\n }\n\n // Update the center and right boundary if needed\n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n\n // Update the maximum length and its center\n if (P[i] > maxLen) {\n maxLen = P[i];\n maxCenter = i;\n }\n }\n\n int start = (maxCenter - maxLen) / 2; // Start index of the longest palindrome\n int end = start + maxLen; // End index of the longest palindrome\n\n return s.substring(start, end);\n }\n}\n```\n\n | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Longest Palindrome | longest-palindromic-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n def expand_around_center(left, right):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return s[left + 1:right]\n longest = ""\n for i in range(len(s)):\n odd_palindrome = expand_around_center(i, i)\n even_palindrome = expand_around_center(i, i+1)\n\n if(len(odd_palindrome) > len(longest)):\n longest = odd_palindrome\n if(len(even_palindrome) > len(longest)):\n longest = even_palindrome\n return longest\n``` | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Longest Palindrome | longest-palindromic-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n def expand_around_center(left, right):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return s[left + 1:right]\n longest = ""\n for i in range(len(s)):\n odd_palindrome = expand_around_center(i, i)\n even_palindrome = expand_around_center(i, i+1)\n\n if(len(odd_palindrome) > len(longest)):\n longest = odd_palindrome\n if(len(even_palindrome) > len(longest)):\n longest = even_palindrome\n return longest\n``` | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Rust 3ms / Python: simple quadratic solution with explanation | longest-palindromic-substring | 0 | 1 | # Intuition\nThere is a linear solution which is called [Manacher algorithm](https://cp-algorithms.com/string/manacher.html). But it is hard to come up with this during the interview.\n\nA very straight forward is a $O(n^2)$ algorihtm in which you try every position and try to expand the string as far as possible. Here I do 2 types of expands separately:\n - starts at `i - 1` and `i + 1`\n - starts at `i`, and `i + 1`\n\nYou can combine them together, but here I do them separately.\n\n# Complexity\n- Time complexity: $O(n^2)$\n- Space complexity: $O(1)$\n\n# Code\n```Rust []\nimpl Solution {\n\n fn expand(s: &[u8], i: usize) -> (usize, usize) {\n let n = s.len();\n \n let (mut i1, mut j1, mut d1) = (i, i + 1, 0);\n while i1 < n && j1 < n && s[i1] == s[j1] {\n i1 -= 1;\n j1 += 1;\n d1 += 2;\n }\n\n let (mut i2, mut j2, mut d2) = (i - 1, i + 1, 1); \n while i2 < n && j2 < n && s[i2] == s[j2] {\n i2 -= 1;\n j2 += 1;\n d2 += 2;\n }\n\n if d1 > d2 {\n return (d1, j1 - d1);\n }\n\n return (d2, j2 - d2);\n }\n\n pub fn longest_palindrome(s: String) -> String {\n let s = s.as_bytes();\n let (mut d_res, mut p_res) = (0, 0);\n\n for i in 0 .. s.len() {\n let (d, p) = Self::expand(s, i);\n if d > d_res {\n d_res = d;\n p_res = p;\n }\n }\n\n return String::from_utf8(s[p_res..p_res + d_res].to_vec()).unwrap();\n }\n}\n```\n```python []\nclass Solution:\n def expand_center(self, s: str, p: int) -> str:\n i = 1\n while p - i >= 0 and p + i < len(s) and s[p - i] == s[p + i]:\n i += 1\n return s[p-i+1:p+i]\n \n \n def expand_neighbors(self, s: str, p: int) -> str:\n if p + 1 >= len(s) or s[p] != s[p + 1]:\n return \'\'\n \n i = 1\n while p - i >= 0 and p + 1 + i < len(s) and s[p - i] == s[p + 1 + i]:\n i += 1\n return s[p-i+1:p+i+1]\n \n def longestPalindrome(self, s: str) -> str:\n if not s:\n return \'\'\n \n best = \'\'\n for p in range(len(s)):\n tmp = self.expand_center(s, p)\n if len(tmp) > len(best):\n best = tmp\n \n tmp = self.expand_neighbors(s, p)\n if len(tmp) > len(best):\n best = tmp\n \n return best\n```\n | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Rust 3ms / Python: simple quadratic solution with explanation | longest-palindromic-substring | 0 | 1 | # Intuition\nThere is a linear solution which is called [Manacher algorithm](https://cp-algorithms.com/string/manacher.html). But it is hard to come up with this during the interview.\n\nA very straight forward is a $O(n^2)$ algorihtm in which you try every position and try to expand the string as far as possible. Here I do 2 types of expands separately:\n - starts at `i - 1` and `i + 1`\n - starts at `i`, and `i + 1`\n\nYou can combine them together, but here I do them separately.\n\n# Complexity\n- Time complexity: $O(n^2)$\n- Space complexity: $O(1)$\n\n# Code\n```Rust []\nimpl Solution {\n\n fn expand(s: &[u8], i: usize) -> (usize, usize) {\n let n = s.len();\n \n let (mut i1, mut j1, mut d1) = (i, i + 1, 0);\n while i1 < n && j1 < n && s[i1] == s[j1] {\n i1 -= 1;\n j1 += 1;\n d1 += 2;\n }\n\n let (mut i2, mut j2, mut d2) = (i - 1, i + 1, 1); \n while i2 < n && j2 < n && s[i2] == s[j2] {\n i2 -= 1;\n j2 += 1;\n d2 += 2;\n }\n\n if d1 > d2 {\n return (d1, j1 - d1);\n }\n\n return (d2, j2 - d2);\n }\n\n pub fn longest_palindrome(s: String) -> String {\n let s = s.as_bytes();\n let (mut d_res, mut p_res) = (0, 0);\n\n for i in 0 .. s.len() {\n let (d, p) = Self::expand(s, i);\n if d > d_res {\n d_res = d;\n p_res = p;\n }\n }\n\n return String::from_utf8(s[p_res..p_res + d_res].to_vec()).unwrap();\n }\n}\n```\n```python []\nclass Solution:\n def expand_center(self, s: str, p: int) -> str:\n i = 1\n while p - i >= 0 and p + i < len(s) and s[p - i] == s[p + i]:\n i += 1\n return s[p-i+1:p+i]\n \n \n def expand_neighbors(self, s: str, p: int) -> str:\n if p + 1 >= len(s) or s[p] != s[p + 1]:\n return \'\'\n \n i = 1\n while p - i >= 0 and p + 1 + i < len(s) and s[p - i] == s[p + 1 + i]:\n i += 1\n return s[p-i+1:p+i+1]\n \n def longestPalindrome(self, s: str) -> str:\n if not s:\n return \'\'\n \n best = \'\'\n for p in range(len(s)):\n tmp = self.expand_center(s, p)\n if len(tmp) > len(best):\n best = tmp\n \n tmp = self.expand_neighbors(s, p)\n if len(tmp) > len(best):\n best = tmp\n \n return best\n```\n | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Daily Leetcoding Challenge 27Beginner Friendly Approach. Understandable.Full Explained 100% working. | longest-palindromic-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhat I thought was basic palindrome solution which we do write.Thought of creating a list which will store the the longest palindromic substring. Here is the Approach\n\n# Beginner Friendly Approach\n<!-- Describe your approach to solving the problem. -->\nThis is Beginner Friendly Approach. Please feel free to ask any question regarding this.\nFirstly,what we can do is check if it is already a palindrome or not using the slicing and basic approach if it is then return that as answer. If not then we will move to else part and we will create new list which will responsible for storing the longesst palindromic substring.Run 2 for Loops then inside for loop check from both the side if both are same then append them to the new list we created.Then sort the list according to the length of the list using key=len.\n\nUpvote If you Liked Solution..Feel Free to ask any doubt \uD83D\uDE0A\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nAs this is Begnner Friendly code so time complexity is O(n^3).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n Space Complexity : O(n^2).\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, a: str) -> str:\n if a==a[::-1]: # checking for already palindrome or not then will return the same \n return a\n else:\n lst=[]\n for i in range(len(a)+1):\n for j in range(i):\n s=(a[j:i])\n if s==s[::-1]:\n lst.append(s)\n lst.sort(key=len)\n return lst[-1]\n``` | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Daily Leetcoding Challenge 27Beginner Friendly Approach. Understandable.Full Explained 100% working. | longest-palindromic-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhat I thought was basic palindrome solution which we do write.Thought of creating a list which will store the the longest palindromic substring. Here is the Approach\n\n# Beginner Friendly Approach\n<!-- Describe your approach to solving the problem. -->\nThis is Beginner Friendly Approach. Please feel free to ask any question regarding this.\nFirstly,what we can do is check if it is already a palindrome or not using the slicing and basic approach if it is then return that as answer. If not then we will move to else part and we will create new list which will responsible for storing the longesst palindromic substring.Run 2 for Loops then inside for loop check from both the side if both are same then append them to the new list we created.Then sort the list according to the length of the list using key=len.\n\nUpvote If you Liked Solution..Feel Free to ask any doubt \uD83D\uDE0A\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nAs this is Begnner Friendly code so time complexity is O(n^3).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n Space Complexity : O(n^2).\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, a: str) -> str:\n if a==a[::-1]: # checking for already palindrome or not then will return the same \n return a\n else:\n lst=[]\n for i in range(len(a)+1):\n for j in range(i):\n s=(a[j:i])\n if s==s[::-1]:\n lst.append(s)\n lst.sort(key=len)\n return lst[-1]\n``` | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
[VIDEO] Visualization of "Expand From Centers" Solution | longest-palindromic-substring | 0 | 1 | https://youtu.be/E-tmN1OM9aA\n\nA brute force solution would first require generating every possible substring, which runs in O(n<sup>2</sup>) time. Then, <i>for each</i> of those substrings, we have to check if they are a palindrome. Since palindromes read the same forwards and backwards, we know that they have to be mirrored across the center. So one way of testing for palindromes is to start in the middle of the string and work outwards, checking at each step to see if the characters are equal. Since each palindrome check runs in O(n), the overall algorithm ends up running in O(n<sup>3</sup>) time.\n\nInstead, we can reduce this to O(n<sup>2</sup>) time by eliminating some redundant steps. This is because we can find the longest palindromic substring for <i>all</i> substrings that have the <i>same</i> center in a single O(n) pass. For example, if the string is `abcdedcfa`, and since we know that `e` is a palindrome by itself, then when we test `ded`, we don\'t need to start from the center again. We can only test the outer characters, the `d`. And when we test `cdedc`, then since we know `ded` is a palindrome, again, we don\'t need to start from the middle again. We can just confirm that the `c`\'s match up.\n\nNow if we expanded one more character, we would see that `b` does NOT equal `f`. Not only does this mean that this substring is not a palindrome, it also means that all other longer palindromes centered on `e` won\'t be palindromes either, so we don\'t need to test the other substrings and we can just exit early.\n\nSo now the question is, how many different centers can a string have? If the length of the substring is odd, then the center could be any of the characters. If the length of the substring is even, then the center could lie <i>between</i> any two characters. So in total, there are 2n - 1 centers (please see the video for a visualization of this).\n\nSo if visiting each center is O(n) and each palindrome check is O(n), then the algorithm now runs in O(n<sup>2</sup>) time.\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s):\n def expand(l, r):\n while l >= 0 and r < len(s) and s[l] == s[r]:\n l -= 1\n r += 1\n return s[l+1:r]\n\n result = ""\n for i in range(len(s)):\n sub1 = expand(i, i)\n if len(sub1) > len(result):\n result = sub1\n sub2 = expand(i, i+1)\n if len(sub2) > len(result):\n result = sub2\n return result\n``` | 6 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
[VIDEO] Visualization of "Expand From Centers" Solution | longest-palindromic-substring | 0 | 1 | https://youtu.be/E-tmN1OM9aA\n\nA brute force solution would first require generating every possible substring, which runs in O(n<sup>2</sup>) time. Then, <i>for each</i> of those substrings, we have to check if they are a palindrome. Since palindromes read the same forwards and backwards, we know that they have to be mirrored across the center. So one way of testing for palindromes is to start in the middle of the string and work outwards, checking at each step to see if the characters are equal. Since each palindrome check runs in O(n), the overall algorithm ends up running in O(n<sup>3</sup>) time.\n\nInstead, we can reduce this to O(n<sup>2</sup>) time by eliminating some redundant steps. This is because we can find the longest palindromic substring for <i>all</i> substrings that have the <i>same</i> center in a single O(n) pass. For example, if the string is `abcdedcfa`, and since we know that `e` is a palindrome by itself, then when we test `ded`, we don\'t need to start from the center again. We can only test the outer characters, the `d`. And when we test `cdedc`, then since we know `ded` is a palindrome, again, we don\'t need to start from the middle again. We can just confirm that the `c`\'s match up.\n\nNow if we expanded one more character, we would see that `b` does NOT equal `f`. Not only does this mean that this substring is not a palindrome, it also means that all other longer palindromes centered on `e` won\'t be palindromes either, so we don\'t need to test the other substrings and we can just exit early.\n\nSo now the question is, how many different centers can a string have? If the length of the substring is odd, then the center could be any of the characters. If the length of the substring is even, then the center could lie <i>between</i> any two characters. So in total, there are 2n - 1 centers (please see the video for a visualization of this).\n\nSo if visiting each center is O(n) and each palindrome check is O(n), then the algorithm now runs in O(n<sup>2</sup>) time.\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s):\n def expand(l, r):\n while l >= 0 and r < len(s) and s[l] == s[r]:\n l -= 1\n r += 1\n return s[l+1:r]\n\n result = ""\n for i in range(len(s)):\n sub1 = expand(i, i)\n if len(sub1) > len(result):\n result = sub1\n sub2 = expand(i, i+1)\n if len(sub2) > len(result):\n result = sub2\n return result\n``` | 6 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | longest-palindromic-substring | 1 | 1 | # Intuition\nUsing two pointers\n\n---\n\n# Solution Video\n\nhttps://youtu.be/aMH1eomKCmE\n\n\u25A0 Timeline of the video\n`0:04` How did you find longest palindromic substring?\n`0:59` What is start point?\n`1:44` Demonstrate how it works with odd case\n`4:36` How do you calculate length of palindrome we found?\n`7:35` Will you pass all test cases?\n`7:53` Consider even case\n`9:03` How to deal with even case\n`11:26` Coding\n`14:52` Explain how to calculate range of palindrome substring\n`17:18` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,844\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\n---\n\n\nFirst of all, Manacher\'s Algorithm solves this question with $$O(n)$$ time. But in real interviews, nobody will come up with such a solution, so I think $$O(n^2)$$ time is enough to pass the interviews.\n\nIf interviewers ask you about a solution with $$O(n)$$. just leave the room. lol\n\n---\n\nSeriously from here, first of all, we need to understand Palindromic Substring.\n\nWhen I think about a solution, I usually start with the small and simple input, because it\'s easy to understand and find a solution. But this time let\'s start with a big input.\n\n```\nInput: "xkarqzghhgfedcbabcdefgzdekx"\n```\n\n---\n\n\u25A0 Question\n\nHow did you find longest palindromic substring?\n\n---\n\nI believe you choose one character, then expand the range to left and right at the same time. If you find longest palindromic substring directly, you are not a human. lol\n\nActually, that is main idea of my solution today. But problem is that we don\'t know where to start. That\'s why we need to shift start point one by one.\n\n---\n\n\u2B50\uFE0F Points\n\nWe need to shift a start point one by one to check longest palindromic substring.\n\n- What is the start point?\n\nSince palindromic substring is like a mirror from some character, it\'s good idea to consider current index as a center of palindromic substring and expand left and right at the same time.\n\nFor example,\n\n```\nInput = "abcba"\n```\nIf we start from `c`, then\n\n```\n"ab" "c" "ba"\n i\n\ni = curerent index\n```\n"ab" and "ba" is a mirror when "c" is center.\n\n---\n\nLet\'s see one by one.\n\n```\nInput = "abcba"\n```\nWe use `left` and `right` pointers. The both pointers start from index `i` but let me start from next to index `i` to make my explanation short. A single character is definitely a palindrome which is length of `1`.\n```\ni = 0\n\n"abcba"\nlir\n \nCheck left(= out of bounds) and right(= "b")\nmax_length = 1 (= "a")\n\n```\n```\ni = 1\n\n"abcba"\n lir\n\nCheck left(= "a") and right(= "c")\nmax_length = 1 (= "a" or "b")\n\n```\n```\ni = 2\n\n"abcba"\n lir\n\nl = 1\nr = 3\nCheck left(= "b") and right(= "b") \u2192 "bcb" is a palindrome.\uD83D\uDE06\n\nLet\'s expand the range!\n\n"abcba"\n l i r\n\nl = 0\nr = 4\nCheck left(= "a") and right(= "a") \u2192 "abcba" is a palindrome.\uD83D\uDE06\nmax_length = 5 (= "abcba")\n\n "abcba"\n l i r\n\nl = -1\nr = 5\nNow left and right are out of bounds, so we finish iteration.\n\n```\n\nLet me skip the cases where we start from later "b" and "a". We already found the max length. (of course solution code will check the later part)\n\n- How do you calculate length of palindrome we found?\n\nFrom the example above, we found `5` as a max length. how do you calculate it? Simply\n\n```\nright - left\n```\nRight? So,\n```\nright - left\n5 - (-1)\n= 6\n```\n\nWait? It\'s longer than max length we found. The reason why this happens is because the two pointers stop at the next position of max length of palindrome.\n\n```\n"abcba"\n l i r\n```\nWhen `i = 2 left = 0 and right = 4`, we found `5` as a max length, but we don\'t know `5` is the max length in the current iteration, so we try to move to the next place to find longer palindrome, even if we don\'t find it in the end.\n\nThat\'s why, left and right pointer always `overrun` and stop at max length in current iteration + 1, so we need to subtract -1 from right - left.\n```\n\u274C right - left\n\uD83D\uDD34 right - left - 1\n```\nBut still you don\'t get it because we have two pointers expanding at the same time? you think we should subtract `-2`?\n\nThis is calculation of index number, so index number usually starts from `0` not `1`, so right - left includes `-1` already. For example,\n\n```\n"aba"\n l r\n```\nActual length is `3`, but if we calculate the length with index number, that should be `2`(index 2 - index 0), so it\'s already including `-1` compared with actual length. That\'s why when we have two pointers and calculate actual length, right - left - 1 works well.\n\nNow you understand main idea of my solution, but I\'m sure you will not pass all cases. Can you geuss why?\n\nThe answer is I explain the case where we have odd length of input string.\n\n---\n\n\u2B50\uFE0F Points\n\nWe have to care about both odd length of input string and even length of input string\n\n---\n\n```\nInput: "abbc"\n ```\nLet\'s see one by one. we can use the same idea. Let me write briefly.\n\n```\n"abbc"\nlir\n\nmax length = 1\n```\n```\n"abbc"\n lir\n\nmax length = 1\n```\n```\n"abbc"\n lir\n\nmax length = 1\n```\n```\n"abbc"\n lir\n\nmax length = 1\n```\n```\n\u274C Output: "a" or "b" or "c" \n```\nOutput should be\n```\n\uD83D\uDD34 Output: "bb" \n```\n- Why this happens?\n\nRegarding odd length of input array, center position of palindrome is definitely on some charcter.\n```\n"abcba", center is "c"\n```\nHow about even length of input string\n```\n"abbc"\nCenter of palindrome is "b | b" \n```\n`|` is center of palindrome. Not on some character.\n\n- So how can you avoid this?\n\nMy idea to avoid this is we start left with current index and right with current index + 1, so we start interation as if we are coming from between the characters. Let me write only when index = 1.\n```\ncurrent index = 1\n\n lr\n"abbc"\n i\n\nWe found palindrome "bb"\n\n l r\n"abbc"\n i\n\nFinish iteration.\n```\nThen\n```\nright - left - 1\n3 - 0 - 1\n= 2(= length of "bb")\n```\n\nWe can use the same idea for both cases but start position is different, that\'s why we call the same function twice in one iteration.\n\nLet\'s see a real algorithm!\n\n### Algorithm Overview:\n1. Initialize `start` and `end` variables to keep track of the starting and ending indices of the longest palindromic substring.\n2. Iterate through each character of the input string `s`.\n3. For each character, expand around it by calling the `expand_around_center` function with two different center possibilities: (i) the current character as the center (odd length palindrome), and (ii) the current character and the next character as the center (even length palindrome).\n4. Compare the lengths of the two expanded palindromes and update `start` and `end` if a longer palindrome is found.\n5. Finally, return the longest palindromic substring by slicing the input string `s` based on the `start` and `end` indices.\n\n### Detailed Explanation:\n1. Check if the input string `s` is empty. If it is, return an empty string, as there can be no palindromic substring in an empty string.\n\n2. Define a helper function `expand_around_center` that takes three arguments: the input string `s`, and two indices `left` and `right`. This function is responsible for expanding the palindrome around the center indices and returns the length of the palindrome.\n\n3. Initialize `start` and `end` variables to 0. These variables will be used to keep track of the indices of the longest palindromic substring found so far.\n\n4. Iterate through each character of the input string `s` using a for loop.\n\n5. Inside the loop, call the `expand_around_center` function twice: once with `i` as the center for an odd length palindrome and once with `i` and `i + 1` as the center for an even length palindrome.\n\n6. Calculate the length of the palindrome for both cases (odd and even) and store them in the `odd` and `even` variables.\n\n7. Calculate the maximum of the lengths of the two palindromes and store it in the `max_len` variable.\n\n8. Check if the `max_len` is greater than the length of the current longest palindromic substring (`end - start`). If it is, update the `start` and `end` variables to include the new longest palindromic substring. The new `start` is set to `i - (max_len - 1) // 2`, and the new `end` is set to `i + max_len // 2`.\n\n9. Continue the loop until all characters in the input string have been processed.\n\n10. After the loop, return the longest palindromic substring by slicing the input string `s` using the `start` and `end` indices. This substring is inclusive of the characters at the `start` and `end` indices.\n\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n "n" is the length of the input string "s." This is because the code uses nested loops. The outer loop runs for each character in the string, and the inner loop, expand_around_center, can potentially run for the entire length of the string in the worst case, leading to a quadratic time complexity.\n\n- Space complexity: $$O(1)$$\n\nthe code uses a constant amount of extra space for variables like "start," "end," "left," "right," and function parameters. The space used does not depend on the size of the input string.\n\n```python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if not s:\n return ""\n\n def expand_around_center(s: str, left: int, right: int):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return right - left - 1\n\n\n start = 0\n end = 0\n\n for i in range(len(s)):\n odd = expand_around_center(s, i, i)\n even = expand_around_center(s, i, i + 1)\n max_len = max(odd, even)\n \n if max_len > end - start:\n start = i - (max_len - 1) // 2\n end = i + max_len // 2\n \n return s[start:end+1]\n```\n```javascript []\n/**\n * @param {string} s\n * @return {string}\n */\nvar longestPalindrome = function(s) {\n if (!s) {\n return "";\n }\n\n function expandAroundCenter(s, left, right) {\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n left--;\n right++;\n }\n return right - left - 1;\n }\n\n let start = 0;\n let end = 0;\n\n for (let i = 0; i < s.length; i++) {\n const odd = expandAroundCenter(s, i, i);\n const even = expandAroundCenter(s, i, i + 1);\n const max_len = Math.max(odd, even);\n\n if (max_len > end - start) {\n start = i - Math.floor((max_len - 1) / 2);\n end = i + Math.floor(max_len / 2);\n }\n }\n\n return s.substring(start, end + 1); \n};\n```\n```java []\nclass Solution {\n public String longestPalindrome(String s) {\n if (s == null || s.length() == 0) {\n return "";\n }\n\n int start = 0;\n int end = 0;\n\n for (int i = 0; i < s.length(); i++) {\n int odd = expandAroundCenter(s, i, i);\n int even = expandAroundCenter(s, i, i + 1);\n int max_len = Math.max(odd, even);\n\n if (max_len > end - start) {\n start = i - (max_len - 1) / 2;\n end = i + max_len / 2;\n }\n }\n\n return s.substring(start, end + 1); \n }\n\n private int expandAroundCenter(String s, int left, int right) {\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n left--;\n right++;\n }\n return right - left - 1;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n string longestPalindrome(string s) {\n if (s.empty()) {\n return "";\n }\n\n int start = 0;\n int end = 0;\n\n for (int i = 0; i < s.length(); i++) {\n int odd = expandAroundCenter(s, i, i);\n int even = expandAroundCenter(s, i, i + 1);\n int max_len = max(odd, even);\n\n if (max_len > end - start) {\n start = i - (max_len - 1) / 2;\n end = i + max_len / 2;\n }\n }\n\n return s.substr(start, end - start + 1); \n }\n\nprivate:\n int expandAroundCenter(string s, int left, int right) {\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n return right - left - 1;\n } \n};\n```\n\nLet me explain this.\n```[]\nif max_len > end - start:\n start = i - (max_len - 1) // 2\n end = i + max_len // 2\n```\nif statement means just when we find longer length.\n\nLet\'s use the same example again.\n```\nInput = "abcba"\n\n```\nWhen `i = 2`, we find 5 as a max length. Let\'s see what will happen.\n\n```[]\nstart = i(2) - (max_len(5) - 1) // 2\nend = i(2) + max_len(5) // 2\n\u2193\nstart = 2 - 2\nend = 2 + 2\n\u2193\nstart = 0\nend = 4\n```\n- Why -1?\n\nThe `-1` is used to calculate the length of the palindrome correctly based on whether it is of odd or even length.\n\nHere, we try to get length of half palindrome except center chracters.\n\nRegarding odd case, actually it works if we don\'t subtract `-1`, because we have only one center chracter and we start from the character.\n\nFor example\n```\n"abcba"\n \u2191\nCenter of palindrome is "c" \n```\nWe will get length of "ab"\n```[]\nno -1 case, 5 // 2 = 2\n-1 case, 4 // 2 = 2\n```\nThe result is the same.\n\nBut regarding even case we start from between characters.\n```\n"abbc"\nCenter of palindrome is "bb" \n```\n\nWe will get length of ""(empty = 0), because center character "bb" itself is whole length of palindrome.\n\n```[]\nno -1 case, 2 // 2 = 1\n-1 case, 1 // 2 = 0\n```\nThe result is different.\n\nIn this case, we have two center charcters, if we remove one character, we can create the same odd case situation from even situaiton, so that we can get correct length except center charcters.\n\nIn this case, i = 1, we get 2 as a max length.\n```\n"abbc"\n```\n\n```[]\nstart = i(1) - (max_len(2) - 1) // 2\nend = i(1) + max_len(2) // 2\n\u2193\nstart = 1 - 0\nend = 1 + 1\n\u2193\nstart = 1\nend = 2\n```\n\nLooks good! \uD83D\uDE06\n\nSince the result is not affected by `-1` in odd case, we subtract `-1` both odd case and even case.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-vowels-permutation/solutions/4218427/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/SFm0hhVCjl8\n\n\u25A0 Timeline of the video\n`0:04` Convert rules to a diagram\n`1:14` How do you count strings with length of n?\n`3:58` Coding\n`7:39` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/binary-trees-with-factors/solutions/4209156/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/LrnKFjcjsqo\n\n\u25A0 Timeline of video\n`0:04` Understand question exactly and approach to solve this question\n`1:33` How can you calculate number of subtrees?\n`4:12` Demonstrate how it works\n`8:40` Coding\n`11:32` Time Complexity and Space Complexity | 33 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | longest-palindromic-substring | 1 | 1 | # Intuition\nUsing two pointers\n\n---\n\n# Solution Video\n\nhttps://youtu.be/aMH1eomKCmE\n\n\u25A0 Timeline of the video\n`0:04` How did you find longest palindromic substring?\n`0:59` What is start point?\n`1:44` Demonstrate how it works with odd case\n`4:36` How do you calculate length of palindrome we found?\n`7:35` Will you pass all test cases?\n`7:53` Consider even case\n`9:03` How to deal with even case\n`11:26` Coding\n`14:52` Explain how to calculate range of palindrome substring\n`17:18` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,844\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\n---\n\n\nFirst of all, Manacher\'s Algorithm solves this question with $$O(n)$$ time. But in real interviews, nobody will come up with such a solution, so I think $$O(n^2)$$ time is enough to pass the interviews.\n\nIf interviewers ask you about a solution with $$O(n)$$. just leave the room. lol\n\n---\n\nSeriously from here, first of all, we need to understand Palindromic Substring.\n\nWhen I think about a solution, I usually start with the small and simple input, because it\'s easy to understand and find a solution. But this time let\'s start with a big input.\n\n```\nInput: "xkarqzghhgfedcbabcdefgzdekx"\n```\n\n---\n\n\u25A0 Question\n\nHow did you find longest palindromic substring?\n\n---\n\nI believe you choose one character, then expand the range to left and right at the same time. If you find longest palindromic substring directly, you are not a human. lol\n\nActually, that is main idea of my solution today. But problem is that we don\'t know where to start. That\'s why we need to shift start point one by one.\n\n---\n\n\u2B50\uFE0F Points\n\nWe need to shift a start point one by one to check longest palindromic substring.\n\n- What is the start point?\n\nSince palindromic substring is like a mirror from some character, it\'s good idea to consider current index as a center of palindromic substring and expand left and right at the same time.\n\nFor example,\n\n```\nInput = "abcba"\n```\nIf we start from `c`, then\n\n```\n"ab" "c" "ba"\n i\n\ni = curerent index\n```\n"ab" and "ba" is a mirror when "c" is center.\n\n---\n\nLet\'s see one by one.\n\n```\nInput = "abcba"\n```\nWe use `left` and `right` pointers. The both pointers start from index `i` but let me start from next to index `i` to make my explanation short. A single character is definitely a palindrome which is length of `1`.\n```\ni = 0\n\n"abcba"\nlir\n \nCheck left(= out of bounds) and right(= "b")\nmax_length = 1 (= "a")\n\n```\n```\ni = 1\n\n"abcba"\n lir\n\nCheck left(= "a") and right(= "c")\nmax_length = 1 (= "a" or "b")\n\n```\n```\ni = 2\n\n"abcba"\n lir\n\nl = 1\nr = 3\nCheck left(= "b") and right(= "b") \u2192 "bcb" is a palindrome.\uD83D\uDE06\n\nLet\'s expand the range!\n\n"abcba"\n l i r\n\nl = 0\nr = 4\nCheck left(= "a") and right(= "a") \u2192 "abcba" is a palindrome.\uD83D\uDE06\nmax_length = 5 (= "abcba")\n\n "abcba"\n l i r\n\nl = -1\nr = 5\nNow left and right are out of bounds, so we finish iteration.\n\n```\n\nLet me skip the cases where we start from later "b" and "a". We already found the max length. (of course solution code will check the later part)\n\n- How do you calculate length of palindrome we found?\n\nFrom the example above, we found `5` as a max length. how do you calculate it? Simply\n\n```\nright - left\n```\nRight? So,\n```\nright - left\n5 - (-1)\n= 6\n```\n\nWait? It\'s longer than max length we found. The reason why this happens is because the two pointers stop at the next position of max length of palindrome.\n\n```\n"abcba"\n l i r\n```\nWhen `i = 2 left = 0 and right = 4`, we found `5` as a max length, but we don\'t know `5` is the max length in the current iteration, so we try to move to the next place to find longer palindrome, even if we don\'t find it in the end.\n\nThat\'s why, left and right pointer always `overrun` and stop at max length in current iteration + 1, so we need to subtract -1 from right - left.\n```\n\u274C right - left\n\uD83D\uDD34 right - left - 1\n```\nBut still you don\'t get it because we have two pointers expanding at the same time? you think we should subtract `-2`?\n\nThis is calculation of index number, so index number usually starts from `0` not `1`, so right - left includes `-1` already. For example,\n\n```\n"aba"\n l r\n```\nActual length is `3`, but if we calculate the length with index number, that should be `2`(index 2 - index 0), so it\'s already including `-1` compared with actual length. That\'s why when we have two pointers and calculate actual length, right - left - 1 works well.\n\nNow you understand main idea of my solution, but I\'m sure you will not pass all cases. Can you geuss why?\n\nThe answer is I explain the case where we have odd length of input string.\n\n---\n\n\u2B50\uFE0F Points\n\nWe have to care about both odd length of input string and even length of input string\n\n---\n\n```\nInput: "abbc"\n ```\nLet\'s see one by one. we can use the same idea. Let me write briefly.\n\n```\n"abbc"\nlir\n\nmax length = 1\n```\n```\n"abbc"\n lir\n\nmax length = 1\n```\n```\n"abbc"\n lir\n\nmax length = 1\n```\n```\n"abbc"\n lir\n\nmax length = 1\n```\n```\n\u274C Output: "a" or "b" or "c" \n```\nOutput should be\n```\n\uD83D\uDD34 Output: "bb" \n```\n- Why this happens?\n\nRegarding odd length of input array, center position of palindrome is definitely on some charcter.\n```\n"abcba", center is "c"\n```\nHow about even length of input string\n```\n"abbc"\nCenter of palindrome is "b | b" \n```\n`|` is center of palindrome. Not on some character.\n\n- So how can you avoid this?\n\nMy idea to avoid this is we start left with current index and right with current index + 1, so we start interation as if we are coming from between the characters. Let me write only when index = 1.\n```\ncurrent index = 1\n\n lr\n"abbc"\n i\n\nWe found palindrome "bb"\n\n l r\n"abbc"\n i\n\nFinish iteration.\n```\nThen\n```\nright - left - 1\n3 - 0 - 1\n= 2(= length of "bb")\n```\n\nWe can use the same idea for both cases but start position is different, that\'s why we call the same function twice in one iteration.\n\nLet\'s see a real algorithm!\n\n### Algorithm Overview:\n1. Initialize `start` and `end` variables to keep track of the starting and ending indices of the longest palindromic substring.\n2. Iterate through each character of the input string `s`.\n3. For each character, expand around it by calling the `expand_around_center` function with two different center possibilities: (i) the current character as the center (odd length palindrome), and (ii) the current character and the next character as the center (even length palindrome).\n4. Compare the lengths of the two expanded palindromes and update `start` and `end` if a longer palindrome is found.\n5. Finally, return the longest palindromic substring by slicing the input string `s` based on the `start` and `end` indices.\n\n### Detailed Explanation:\n1. Check if the input string `s` is empty. If it is, return an empty string, as there can be no palindromic substring in an empty string.\n\n2. Define a helper function `expand_around_center` that takes three arguments: the input string `s`, and two indices `left` and `right`. This function is responsible for expanding the palindrome around the center indices and returns the length of the palindrome.\n\n3. Initialize `start` and `end` variables to 0. These variables will be used to keep track of the indices of the longest palindromic substring found so far.\n\n4. Iterate through each character of the input string `s` using a for loop.\n\n5. Inside the loop, call the `expand_around_center` function twice: once with `i` as the center for an odd length palindrome and once with `i` and `i + 1` as the center for an even length palindrome.\n\n6. Calculate the length of the palindrome for both cases (odd and even) and store them in the `odd` and `even` variables.\n\n7. Calculate the maximum of the lengths of the two palindromes and store it in the `max_len` variable.\n\n8. Check if the `max_len` is greater than the length of the current longest palindromic substring (`end - start`). If it is, update the `start` and `end` variables to include the new longest palindromic substring. The new `start` is set to `i - (max_len - 1) // 2`, and the new `end` is set to `i + max_len // 2`.\n\n9. Continue the loop until all characters in the input string have been processed.\n\n10. After the loop, return the longest palindromic substring by slicing the input string `s` using the `start` and `end` indices. This substring is inclusive of the characters at the `start` and `end` indices.\n\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n "n" is the length of the input string "s." This is because the code uses nested loops. The outer loop runs for each character in the string, and the inner loop, expand_around_center, can potentially run for the entire length of the string in the worst case, leading to a quadratic time complexity.\n\n- Space complexity: $$O(1)$$\n\nthe code uses a constant amount of extra space for variables like "start," "end," "left," "right," and function parameters. The space used does not depend on the size of the input string.\n\n```python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if not s:\n return ""\n\n def expand_around_center(s: str, left: int, right: int):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return right - left - 1\n\n\n start = 0\n end = 0\n\n for i in range(len(s)):\n odd = expand_around_center(s, i, i)\n even = expand_around_center(s, i, i + 1)\n max_len = max(odd, even)\n \n if max_len > end - start:\n start = i - (max_len - 1) // 2\n end = i + max_len // 2\n \n return s[start:end+1]\n```\n```javascript []\n/**\n * @param {string} s\n * @return {string}\n */\nvar longestPalindrome = function(s) {\n if (!s) {\n return "";\n }\n\n function expandAroundCenter(s, left, right) {\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n left--;\n right++;\n }\n return right - left - 1;\n }\n\n let start = 0;\n let end = 0;\n\n for (let i = 0; i < s.length; i++) {\n const odd = expandAroundCenter(s, i, i);\n const even = expandAroundCenter(s, i, i + 1);\n const max_len = Math.max(odd, even);\n\n if (max_len > end - start) {\n start = i - Math.floor((max_len - 1) / 2);\n end = i + Math.floor(max_len / 2);\n }\n }\n\n return s.substring(start, end + 1); \n};\n```\n```java []\nclass Solution {\n public String longestPalindrome(String s) {\n if (s == null || s.length() == 0) {\n return "";\n }\n\n int start = 0;\n int end = 0;\n\n for (int i = 0; i < s.length(); i++) {\n int odd = expandAroundCenter(s, i, i);\n int even = expandAroundCenter(s, i, i + 1);\n int max_len = Math.max(odd, even);\n\n if (max_len > end - start) {\n start = i - (max_len - 1) / 2;\n end = i + max_len / 2;\n }\n }\n\n return s.substring(start, end + 1); \n }\n\n private int expandAroundCenter(String s, int left, int right) {\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n left--;\n right++;\n }\n return right - left - 1;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n string longestPalindrome(string s) {\n if (s.empty()) {\n return "";\n }\n\n int start = 0;\n int end = 0;\n\n for (int i = 0; i < s.length(); i++) {\n int odd = expandAroundCenter(s, i, i);\n int even = expandAroundCenter(s, i, i + 1);\n int max_len = max(odd, even);\n\n if (max_len > end - start) {\n start = i - (max_len - 1) / 2;\n end = i + max_len / 2;\n }\n }\n\n return s.substr(start, end - start + 1); \n }\n\nprivate:\n int expandAroundCenter(string s, int left, int right) {\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n return right - left - 1;\n } \n};\n```\n\nLet me explain this.\n```[]\nif max_len > end - start:\n start = i - (max_len - 1) // 2\n end = i + max_len // 2\n```\nif statement means just when we find longer length.\n\nLet\'s use the same example again.\n```\nInput = "abcba"\n\n```\nWhen `i = 2`, we find 5 as a max length. Let\'s see what will happen.\n\n```[]\nstart = i(2) - (max_len(5) - 1) // 2\nend = i(2) + max_len(5) // 2\n\u2193\nstart = 2 - 2\nend = 2 + 2\n\u2193\nstart = 0\nend = 4\n```\n- Why -1?\n\nThe `-1` is used to calculate the length of the palindrome correctly based on whether it is of odd or even length.\n\nHere, we try to get length of half palindrome except center chracters.\n\nRegarding odd case, actually it works if we don\'t subtract `-1`, because we have only one center chracter and we start from the character.\n\nFor example\n```\n"abcba"\n \u2191\nCenter of palindrome is "c" \n```\nWe will get length of "ab"\n```[]\nno -1 case, 5 // 2 = 2\n-1 case, 4 // 2 = 2\n```\nThe result is the same.\n\nBut regarding even case we start from between characters.\n```\n"abbc"\nCenter of palindrome is "bb" \n```\n\nWe will get length of ""(empty = 0), because center character "bb" itself is whole length of palindrome.\n\n```[]\nno -1 case, 2 // 2 = 1\n-1 case, 1 // 2 = 0\n```\nThe result is different.\n\nIn this case, we have two center charcters, if we remove one character, we can create the same odd case situation from even situaiton, so that we can get correct length except center charcters.\n\nIn this case, i = 1, we get 2 as a max length.\n```\n"abbc"\n```\n\n```[]\nstart = i(1) - (max_len(2) - 1) // 2\nend = i(1) + max_len(2) // 2\n\u2193\nstart = 1 - 0\nend = 1 + 1\n\u2193\nstart = 1\nend = 2\n```\n\nLooks good! \uD83D\uDE06\n\nSince the result is not affected by `-1` in odd case, we subtract `-1` both odd case and even case.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/count-vowels-permutation/solutions/4218427/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/SFm0hhVCjl8\n\n\u25A0 Timeline of the video\n`0:04` Convert rules to a diagram\n`1:14` How do you count strings with length of n?\n`3:58` Coding\n`7:39` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/binary-trees-with-factors/solutions/4209156/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/LrnKFjcjsqo\n\n\u25A0 Timeline of video\n`0:04` Understand question exactly and approach to solve this question\n`1:33` How can you calculate number of subtrees?\n`4:12` Demonstrate how it works\n`8:40` Coding\n`11:32` Time Complexity and Space Complexity | 33 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
🔥Expand Around Center & 🔥100% Manacher's Algorithm | Java | C++ | Py | Js| C# | PHP | longest-palindromic-substring | 1 | 1 | # 1st Method :- Expand Around Center \uD83D\uDEA9\n## Intuition \uD83D\uDE80:\n\nThe intuition behind this code is to find the longest palindromic substring within a given input string `s`. A palindromic substring is a string that reads the same forwards and backward. To achieve this, the code explores the input string character by character, checking both odd and even-length palindromes by expanding around the center of each character and updating the longest palindrome found so far.\n\n## Approach \uD83D\uDE80:\n\n1. **Initialization**: \n - Check if the input string `s` is empty. If it is, return an empty string because there can\'t be any palindromes in an empty string.\n - Initialize a variable `longestPalindromeIndices` to store the indices of the longest palindrome found. Initially, it\'s set to [0, 0].\n\n2. **Main Loop**:\n - Iterate through the characters of the input string `s` using a for loop.\n\n3. **Odd-Length Palindromes**:\n - For each character at position `i`, check if there is a palindrome centered at that character. This is done by calling the `expandAroundCenter` function with `i` as both the start and end positions.\n - If a longer palindrome is found than the current longest one, update `longestPalindromeIndices` with the new indices.\n\n4. **Even-Length Palindromes**:\n - Check if there is a palindrome centered between the characters at positions `i` and `i + 1`. This is done by calling the `expandAroundCenter` function with `i` as the start position and `i + 1` as the end position.\n - If a longer even-length palindrome is found, update `longestPalindromeIndices` with the new indices.\n\n5. **Continuation**:\n - Continue this process for all characters in the input string. By the end of the loop, you will have identified the indices of the longest palindromic substring.\n\n6. **Result Extraction**:\n - Finally, extract the longest palindromic substring from the input string `s` using the indices obtained in `longestPalindromeIndices`.\n - Return this extracted substring as the result.\n\nThe key idea is to systematically explore the input string, checking both odd and even-length palindromes by expanding around the center of each character and maintaining the information about the longest palindrome found throughout the process. This approach ensures that you find the maximum length palindromic substring within the input string.\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9 Time complexity: O(N^2)\n\n1. The `expandAroundCenter` function has a time complexity of O(N), where N is the length of the input string `s`. This is because in the worst case, it can expand all the way to the ends of the string.\n2. The `longestPalindrome` function iterates through the characters of the string, and for each character, it may call `expandAroundCenter` once or twice (in the case of even-length palindromes). Therefore, the time complexity of the `longestPalindrome` function is O(N^2).\n\nSo, the overall time complexity of the code is O(N^2) due to the nested loops in the `longestPalindrome` function.\n\n### \uD83C\uDFF9 Space complexity: O(1)\n\nThe space complexity is primarily determined by the additional space used for variables and the recursive call stack.\n\n1. The `expandAroundCenter` function uses a constant amount of extra space, so its space complexity is O(1).\n2. The `longestPalindrome` function uses a few additional integer variables to store indices, but the space used by these variables is also constant, so its space complexity is O(1).\n3. The recursive calls in the `expandAroundCenter` function do not use significant additional space because they are tail-recursive. The stack space used by these calls is O(1).\n\nSo, the overall space complexity of the code is O(1).\n\n## Code \u2712\uFE0F\n``` Java []\nclass Solution {\n public String longestPalindrome(String s) {\n // Check if the input string is empty, return an empty string if so\n if (s.isEmpty())\n return "";\n\n // Initialize variables to store the indices of the longest palindrome found\n int[] longestPalindromeIndices = { 0, 0 };\n\n // Loop through the characters in the input string\n for (int i = 0; i < s.length(); ++i) {\n // Find the indices of the longest palindrome centered at character i\n int[] currentIndices = expandAroundCenter(s, i, i);\n\n // Compare the length of the current palindrome with the longest found so far\n if (currentIndices[1] - currentIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the current one is longer\n longestPalindromeIndices = currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if (i + 1 < s.length() && s.charAt(i) == s.charAt(i + 1)) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n int[] evenIndices = expandAroundCenter(s, i, i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so\n // far\n if (evenIndices[1] - evenIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the even-length one is longer\n longestPalindromeIndices = evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return s.substring(longestPalindromeIndices[0], longestPalindromeIndices[1] + 1);\n }\n\n // Helper function to find and return the indices of the longest palindrome\n // extended from s[i..j] (inclusive) by expanding around the center\n private int[] expandAroundCenter(final String s, int i, int j) {\n // Expand the palindrome by moving outward from the center while the characters\n // match\n while (i >= 0 && j < s.length() && s.charAt(i) == s.charAt(j)) {\n i--; // Move the left index to the left\n j++; // Move the right index to the right\n }\n // Return the indices of the longest palindrome found\n return new int[] { i + 1, j - 1 };\n }\n}\n\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n // Check if the input string is empty, return an empty string if so\n if (s.empty())\n return "";\n\n // Initialize variables to store the indices of the longest palindrome found\n std::vector<int> longestPalindromeIndices = {0, 0};\n\n for (int i = 0; i < s.length(); ++i) {\n // Find the indices of the longest palindrome centered at character i\n std::vector<int> currentIndices = expandAroundCenter(s, i, i);\n\n // Compare the length of the current palindrome with the longest found so far\n if (currentIndices[1] - currentIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n longestPalindromeIndices = currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if (i + 1 < s.length() && s[i] == s[i + 1]) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n std::vector<int> evenIndices = expandAroundCenter(s, i, i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so far\n if (evenIndices[1] - evenIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n longestPalindromeIndices = evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return s.substr(longestPalindromeIndices[0], longestPalindromeIndices[1] - longestPalindromeIndices[0] + 1);\n }\n\nprivate:\n // Helper function to find and return the indices of the longest palindrome\n // extended from s[i..j] (inclusive) by expanding around the center\n std::vector<int> expandAroundCenter(const std::string &s, int i, int j) {\n while (i >= 0 && j < s.length() && s[i] == s[j]) {\n --i;\n ++j;\n }\n return {i + 1, j - 1};\n }\n};\n\n```\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n # Check if the input string is empty, return an empty string if so\n if not s:\n return ""\n\n # Initialize variables to store the indices of the longest palindrome found\n longest_palindrome_indices = [0, 0]\n\n def expand_around_center(s, i, j):\n # Helper function to find and return the indices of the longest palindrome\n # extended from s[i..j] (inclusive) by expanding around the center\n while i >= 0 and j < len(s) and s[i] == s[j]:\n i -= 1\n j += 1\n return [i + 1, j - 1]\n\n for i in range(len(s)):\n current_indices = expand_around_center(s, i, i)\n\n # Compare the length of the current palindrome with the longest found so far\n if current_indices[1] - current_indices[0] > longest_palindrome_indices[1] - longest_palindrome_indices[0]:\n longest_palindrome_indices = current_indices\n\n if i + 1 < len(s) and s[i] == s[i + 1]:\n even_indices = expand_around_center(s, i, i + 1)\n\n # Compare the length of the even-length palindrome with the longest found so far\n if even_indices[1] - even_indices[0] > longest_palindrome_indices[1] - longest_palindrome_indices[0]:\n longest_palindrome_indices = even_indices\n\n # Extract and return the longest palindrome substring using the indices\n return s[longest_palindrome_indices[0]:longest_palindrome_indices[1] + 1]\n\n```\n``` JavaScript []\nvar longestPalindrome = function(s) {\n // Check if the input string is empty, return an empty string if so\n if (s.length === 0)\n return "";\n\n // Initialize variables to store the indices of the longest palindrome found\n let longestPalindromeIndices = [0, 0];\n\n // Loop through the characters in the input string\n for (let i = 0; i < s.length; ++i) {\n // Find the indices of the longest palindrome centered at character i\n let currentIndices = expandAroundCenter(s, i, i);\n\n // Compare the length of the current palindrome with the longest found so far\n if (currentIndices[1] - currentIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the current one is longer\n longestPalindromeIndices = currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if (i + 1 < s.length && s[i] === s[i + 1]) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n let evenIndices = expandAroundCenter(s, i, i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so\n // far\n if (evenIndices[1] - evenIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the even-length one is longer\n longestPalindromeIndices = evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return s.slice(longestPalindromeIndices[0], longestPalindromeIndices[1] + 1);\n}\n\n// Helper function to find and return the indices of the longest palindrome\n// extended from s[i..j] (inclusive) by expanding around the center\nfunction expandAroundCenter(s, i, j) {\n // Expand the palindrome by moving outward from the center while the characters match\n while (i >= 0 && j < s.length && s[i] === s[j]) {\n i--; // Move the left index to the left\n j++; // Move the right index to the right\n }\n // Return the indices of the longest palindrome found\n return [i + 1, j - 1];\n}\n\n```\n``` C# []\npublic class Solution {\n public string LongestPalindrome(string s) {\n // Check if the input string is empty, return an empty string if so\n if (string.IsNullOrEmpty(s))\n return "";\n\n // Initialize variables to store the indices of the longest palindrome found\n int[] longestPalindromeIndices = { 0, 0 };\n\n // Loop through the characters in the input string\n for (int i = 0; i < s.Length; ++i) {\n // Find the indices of the longest palindrome centered at character i\n int[] currentIndices = ExpandAroundCenter(s, i, i);\n\n // Compare the length of the current palindrome with the longest found so far\n if (currentIndices[1] - currentIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the current one is longer\n longestPalindromeIndices = currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if (i + 1 < s.Length && s[i] == s[i + 1]) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n int[] evenIndices = ExpandAroundCenter(s, i, i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so\n // far\n if (evenIndices[1] - evenIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the even-length one is longer\n longestPalindromeIndices = evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return s.Substring(longestPalindromeIndices[0], longestPalindromeIndices[1] - longestPalindromeIndices[0] + 1);\n }\n\n // Helper function to find and return the indices of the longest palindrome\n // extended from s[i..j] (inclusive) by expanding around the center\n private int[] ExpandAroundCenter(string s, int i, int j) {\n // Expand the palindrome by moving outward from the center while the characters match\n while (i >= 0 && j < s.Length && s[i] == s[j]) {\n i--; // Move the left index to the left\n j++; // Move the right index to the right\n }\n // Return the indices of the longest palindrome found\n return new int[] { i + 1, j - 1 };\n }\n}\n```\n``` PHP []\nclass Solution {\n public function longestPalindrome($s) {\n // Check if the input string is empty, return an empty string if so\n if (empty($s)) {\n return "";\n }\n\n // Initialize variables to store the indices of the longest palindrome found\n $longestPalindromeIndices = array(0, 0);\n\n // Loop through the characters in the input string\n for ($i = 0; $i < strlen($s); ++$i) {\n // Find the indices of the longest palindrome centered at character i\n $currentIndices = $this->expandAroundCenter($s, $i, $i);\n\n // Compare the length of the current palindrome with the longest found so far\n if ($currentIndices[1] - $currentIndices[0] > $longestPalindromeIndices[1] - $longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the current one is longer\n $longestPalindromeIndices = $currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if ($i + 1 < strlen($s) && $s[$i] == $s[$i + 1]) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n $evenIndices = $this->expandAroundCenter($s, $i, $i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so\n // far\n if ($evenIndices[1] - $evenIndices[0] > $longestPalindromeIndices[1] - $longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the even-length one is longer\n $longestPalindromeIndices = $evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return substr($s, $longestPalindromeIndices[0], $longestPalindromeIndices[1] - $longestPalindromeIndices[0] + 1);\n }\n\n // Helper function to find and return the indices of the longest palindrome\n // extended from s[i..j] (inclusive) by expanding around the center\n private function expandAroundCenter($s, $i, $j) {\n // Expand the palindrome by moving outward from the center while the characters match\n while ($i >= 0 && $j < strlen($s) && $s[$i] == $s[$j]) {\n $i--; // Move the left index to the left\n $j++; // Move the right index to the right\n }\n // Return the indices of the longest palindrome found\n return array($i + 1, $j - 1);\n }\n}\n```\n\n\n---\n\n# 2nd Method :- Manacher\'s Algorithm \uD83D\uDEA9\n\n## Intuition \uD83D\uDE80:\nThe code implements Manacher\'s algorithm, which is designed to find the longest palindromic substring in a given string. The algorithm is an efficient way to tackle this problem and is based on the following key ideas:\n\n1. Utilize symmetry: Palindromes have a property of symmetry, which means their left and right sides are mirror images of each other. Manacher\'s algorithm takes advantage of this property to optimize the process.\n\n2. Avoid redundant computations: The algorithm uses previously computed information to avoid redundant checks, which makes it more efficient than brute force methods.\n\n## Approach \uD83D\uDE80:\n\n1. **Preprocessing**:\n - The input string `s` is preprocessed to create a modified string `T` with special characters (^, #, and dollar ) inserted between each character to simplify palindrome detection.\n\n2. **Initialization**:\n - Initialize variables:\n - `strLength` for the length of the modified string `T`.\n - `palindromeLengths`, an array to store the lengths of palindromes centered at each position in `T`.\n - `center` for the current center of the palindrome being processed.\n - `rightEdge` for the rightmost edge of the palindrome found so far.\n\n3. **Palindrome Detection**:\n - Loop through the modified string `T` to find palindromes centered at each position.\n - Calculate the length of the palindrome at the current position `i` based on previously computed information and expand it if possible. This is done by comparing characters around the current position.\n - Update `center` and `rightEdge` if a longer palindrome is found.\n\n4. **Find the Longest Palindrome**:\n - After processing the entire modified string `T`, identify the longest palindrome by searching the `palindromeLengths` array for the maximum value.\n - Determine the center of this longest palindrome.\n\n5. **Extract the Result**:\n - Use the information about the longest palindrome (center and length) in the modified string `T` to extract the corresponding substring from the original input string `s`.\n\nThe code effectively implements this approach to find and return the longest palindromic substring in the input string `s`. Manacher\'s algorithm is more efficient than naive methods because it takes advantage of the properties of palindromes and avoids redundant comparisons, making it a good choice for solving this problem.\n\n\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9 Time complexity: O(N)\nThe time complexity of Manacher\'s algorithm is O(N), where N is the length of the input string `s`. This is because the algorithm processes each character of the modified string exactly once (with some constant factor overhead) in a linear pass. The key factor in achieving this efficiency is the "center expansion" technique used to find palindromes, which avoids unnecessary character comparisons. \n\n### \uD83C\uDFF9 Space complexity: O(N)\nThe space complexity of the code is O(N) as well. This is primarily due to the creation of the modified string `T`, which is constructed by adding extra characters, such as \'^\', \'#\', and \'$\', to the original string. The `P` array used to store the lengths of palindromes at each position also has a space complexity of O(N) because it is an array of the same length as the modified string. The other variables used in the algorithm (e.g., `C`, `R`, and loop counters) have constant space requirements and do not significantly contribute to the space complexity.\n\nSo, in terms of both time and space complexity, this code is very efficient for finding the longest palindromic substring in a string.\n\n\n## Code \u2712\uFE0F\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n // Step 1: Preprocess the input string\n StringBuilder processedStr = new StringBuilder("^#");\n for (char c : s.toCharArray()) {\n processedStr.append(c).append("#");\n }\n processedStr.append("$");\n String modifiedString = processedStr.toString();\n\n // Step 2: Initialize variables for the algorithm\n int strLength = modifiedString.length();\n int[] palindromeLengths = new int[strLength];\n int center = 0; // Current center of the palindrome\n int rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for (int i = 1; i < strLength - 1; i++) {\n palindromeLengths[i] = (rightEdge > i) ? Math.min(rightEdge - i, palindromeLengths[2 * center - i]) : 0;\n \n // Expand the palindrome around the current character\n while (modifiedString.charAt(i + 1 + palindromeLengths[i]) == modifiedString.charAt(i - 1 - palindromeLengths[i])) {\n palindromeLengths[i]++;\n }\n \n // Update the rightmost edge and center if necessary\n if (i + palindromeLengths[i] > rightEdge) {\n center = i;\n rightEdge = i + palindromeLengths[i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n int maxLength = 0;\n int maxCenter = 0;\n for (int i = 0; i < strLength; i++) {\n if (palindromeLengths[i] > maxLength) {\n maxLength = palindromeLengths[i];\n maxCenter = i;\n }\n }\n \n // Step 5: Extract the longest palindrome from the modified string\n int start = (maxCenter - maxLength) / 2;\n int end = start + maxLength;\n\n // Return the longest palindrome in the original string\n return s.substring(start, end);\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n // Step 1: Preprocess the input string\n std::string processedStr = "^#";\n for (char c : s) {\n processedStr.push_back(c);\n processedStr.push_back(\'#\');\n }\n processedStr.push_back(\'$\');\n\n // Step 2: Initialize variables for the algorithm\n int strLength = processedStr.length();\n std::vector<int> palindromeLengths(strLength, 0);\n int center = 0; // Current center of the palindrome\n int rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for (int i = 1; i < strLength - 1; i++) {\n palindromeLengths[i] = (rightEdge > i) ? std::min(rightEdge - i, palindromeLengths[2 * center - i]) : 0;\n\n // Expand the palindrome around the current character\n while (processedStr[i + 1 + palindromeLengths[i]] == processedStr[i - 1 - palindromeLengths[i]]) {\n palindromeLengths[i]++;\n }\n\n // Update the rightmost edge and center if necessary\n if (i + palindromeLengths[i] > rightEdge) {\n center = i;\n rightEdge = i + palindromeLengths[i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n int maxLength = 0;\n int maxCenter = 0;\n for (int i = 0; i < strLength; i++) {\n if (palindromeLengths[i] > maxLength) {\n maxLength = palindromeLengths[i];\n maxCenter = i;\n }\n }\n\n // Step 5: Extract the longest palindrome from the modified string\n int start = (maxCenter - maxLength) / 2;\n int end = start + maxLength;\n\n // Return the longest palindrome in the original string\n return s.substr(start, end - start);\n }\n};\n```\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n # Step 1: Preprocess the input string\n processed_str = "^#"\n for c in s:\n processed_str += c + "#"\n processed_str += "$"\n\n # Step 2: Initialize variables for the algorithm\n str_length = len(processed_str)\n palindrome_lengths = [0] * str_length\n center = 0 # Current center of the palindrome\n right_edge = 0 # Rightmost edge of the palindrome\n\n # Step 3: Loop through the modified string to find palindromes\n for i in range(1, str_length - 1):\n palindrome_lengths[i] = min(right_edge - i, palindrome_lengths[2 * center - i]) if right_edge > i else 0\n\n # Expand the palindrome around the current character\n while processed_str[i + 1 + palindrome_lengths[i]] == processed_str[i - 1 - palindrome_lengths[i]]:\n palindrome_lengths[i] += 1\n\n # Update the rightmost edge and center if necessary\n if i + palindrome_lengths[i] > right_edge:\n center = i\n right_edge = i + palindrome_lengths[i]\n\n # Step 4: Find the longest palindrome and its center\n max_length = 0\n max_center = 0\n for i in range(str_length):\n if palindrome_lengths[i] > max_length:\n max_length = palindrome_lengths[i]\n max_center = i\n\n # Step 5: Extract the longest palindrome from the modified string\n start = (max_center - max_length) // 2\n end = start + max_length\n\n # Return the longest palindrome in the original string\n return s[start:end]\n```\n``` JavaScript []\nclass Solution {\n longestPalindrome(s) {\n // Step 1: Preprocess the input string\n let processedStr = "^#";\n for (let i = 0; i < s.length; i++) {\n processedStr += s[i] + "#";\n }\n processedStr += "$";\n let modifiedString = processedStr;\n\n // Step 2: Initialize variables for the algorithm\n let strLength = modifiedString.length;\n let palindromeLengths = new Array(strLength).fill(0);\n let center = 0; // Current center of the palindrome\n let rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for (let i = 1; i < strLength - 1; i++) {\n palindromeLengths[i] = (rightEdge > i) ? Math.min(rightEdge - i, palindromeLengths[2 * center - i]) : 0;\n\n // Expand the palindrome around the current character\n while (modifiedString[i + 1 + palindromeLengths[i]] === modifiedString[i - 1 - palindromeLengths[i]]) {\n palindromeLengths[i]++;\n }\n\n // Update the rightmost edge and center if necessary\n if (i + palindromeLengths[i] > rightEdge) {\n center = i;\n rightEdge = i + palindromeLengths[i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n let maxLength = 0;\n let maxCenter = 0;\n for (let i = 0; i < strLength; i++) {\n if (palindromeLengths[i] > maxLength) {\n maxLength = palindromeLengths[i];\n maxCenter = i;\n }\n }\n\n // Step 5: Extract the longest palindrome from the modified string\n let start = (maxCenter - maxLength) / 2;\n let end = start + maxLength;\n\n // Return the longest palindrome in the original string\n return s.substring(start, end);\n }\n}\n```\n``` C# []\npublic class Solution {\n public string LongestPalindrome(string s) {\n // Step 1: Preprocess the input string\n StringBuilder processedStr = new StringBuilder("^#");\n foreach (char c in s) {\n processedStr.Append(c).Append("#");\n }\n processedStr.Append("$");\n string modifiedString = processedStr.ToString();\n\n // Step 2: Initialize variables for the algorithm\n int strLength = modifiedString.Length;\n int[] palindromeLengths = new int[strLength];\n int center = 0; // Current center of the palindrome\n int rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for (int i = 1; i < strLength - 1; i++) {\n palindromeLengths[i] = (rightEdge > i) ? Math.Min(rightEdge - i, palindromeLengths[2 * center - i]) : 0;\n\n // Expand the palindrome around the current character\n while (modifiedString[i + 1 + palindromeLengths[i]] == modifiedString[i - 1 - palindromeLengths[i]]) {\n palindromeLengths[i]++;\n }\n\n // Update the rightmost edge and center if necessary\n if (i + palindromeLengths[i] > rightEdge) {\n center = i;\n rightEdge = i + palindromeLengths[i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n int maxLength = 0;\n int maxCenter = 0;\n for (int i = 0; i < strLength; i++) {\n if (palindromeLengths[i] > maxLength) {\n maxLength = palindromeLengths[i];\n maxCenter = i;\n }\n }\n\n // Step 5: Extract the longest palindrome from the modified string\n int start = (maxCenter - maxLength) / 2;\n int end = start + maxLength;\n\n // Return the longest palindrome in the original string\n return s.Substring(start, end - start);\n }\n}\n```\n``` PHP []\nclass Solution {\n public function longestPalindrome($s) {\n // Step 1: Preprocess the input string\n $processedStr = "^#";\n for ($i = 0; $i < strlen($s); $i++) {\n $processedStr .= $s[$i] . "#";\n }\n $processedStr .= "$";\n $modifiedString = $processedStr;\n\n // Step 2: Initialize variables for the algorithm\n $strLength = strlen($modifiedString);\n $palindromeLengths = array_fill(0, $strLength, 0);\n $center = 0; // Current center of the palindrome\n $rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for ($i = 1; $i < $strLength - 1; $i++) {\n $palindromeLengths[$i] = ($rightEdge > $i) ? min($rightEdge - $i, $palindromeLengths[2 * $center - $i]) : 0;\n\n // Expand the palindrome around the current character\n while ($modifiedString[$i + 1 + $palindromeLengths[$i]] == $modifiedString[$i - 1 - $palindromeLengths[$i]]) {\n $palindromeLengths[$i]++;\n }\n\n // Update the rightmost edge and center if necessary\n if ($i + $palindromeLengths[$i] > $rightEdge) {\n $center = $i;\n $rightEdge = $i + $palindromeLengths[$i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n $maxLength = 0;\n $maxCenter = 0;\n for ($i = 0; $i < $strLength; $i++) {\n if ($palindromeLengths[$i] > $maxLength) {\n $maxLength = $palindromeLengths[$i];\n $maxCenter = $i;\n }\n }\n\n // Step 5: Extract the longest palindrome from the modified string\n $start = ($maxCenter - $maxLength) / 2;\n $end = $start + $maxLength;\n\n // Return the longest palindrome in the original string\n return substr($s, $start, $end - $start);\n }\n}\n```\n\n\n# Up Vote Guys\n | 45 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
🔥Expand Around Center & 🔥100% Manacher's Algorithm | Java | C++ | Py | Js| C# | PHP | longest-palindromic-substring | 1 | 1 | # 1st Method :- Expand Around Center \uD83D\uDEA9\n## Intuition \uD83D\uDE80:\n\nThe intuition behind this code is to find the longest palindromic substring within a given input string `s`. A palindromic substring is a string that reads the same forwards and backward. To achieve this, the code explores the input string character by character, checking both odd and even-length palindromes by expanding around the center of each character and updating the longest palindrome found so far.\n\n## Approach \uD83D\uDE80:\n\n1. **Initialization**: \n - Check if the input string `s` is empty. If it is, return an empty string because there can\'t be any palindromes in an empty string.\n - Initialize a variable `longestPalindromeIndices` to store the indices of the longest palindrome found. Initially, it\'s set to [0, 0].\n\n2. **Main Loop**:\n - Iterate through the characters of the input string `s` using a for loop.\n\n3. **Odd-Length Palindromes**:\n - For each character at position `i`, check if there is a palindrome centered at that character. This is done by calling the `expandAroundCenter` function with `i` as both the start and end positions.\n - If a longer palindrome is found than the current longest one, update `longestPalindromeIndices` with the new indices.\n\n4. **Even-Length Palindromes**:\n - Check if there is a palindrome centered between the characters at positions `i` and `i + 1`. This is done by calling the `expandAroundCenter` function with `i` as the start position and `i + 1` as the end position.\n - If a longer even-length palindrome is found, update `longestPalindromeIndices` with the new indices.\n\n5. **Continuation**:\n - Continue this process for all characters in the input string. By the end of the loop, you will have identified the indices of the longest palindromic substring.\n\n6. **Result Extraction**:\n - Finally, extract the longest palindromic substring from the input string `s` using the indices obtained in `longestPalindromeIndices`.\n - Return this extracted substring as the result.\n\nThe key idea is to systematically explore the input string, checking both odd and even-length palindromes by expanding around the center of each character and maintaining the information about the longest palindrome found throughout the process. This approach ensures that you find the maximum length palindromic substring within the input string.\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9 Time complexity: O(N^2)\n\n1. The `expandAroundCenter` function has a time complexity of O(N), where N is the length of the input string `s`. This is because in the worst case, it can expand all the way to the ends of the string.\n2. The `longestPalindrome` function iterates through the characters of the string, and for each character, it may call `expandAroundCenter` once or twice (in the case of even-length palindromes). Therefore, the time complexity of the `longestPalindrome` function is O(N^2).\n\nSo, the overall time complexity of the code is O(N^2) due to the nested loops in the `longestPalindrome` function.\n\n### \uD83C\uDFF9 Space complexity: O(1)\n\nThe space complexity is primarily determined by the additional space used for variables and the recursive call stack.\n\n1. The `expandAroundCenter` function uses a constant amount of extra space, so its space complexity is O(1).\n2. The `longestPalindrome` function uses a few additional integer variables to store indices, but the space used by these variables is also constant, so its space complexity is O(1).\n3. The recursive calls in the `expandAroundCenter` function do not use significant additional space because they are tail-recursive. The stack space used by these calls is O(1).\n\nSo, the overall space complexity of the code is O(1).\n\n## Code \u2712\uFE0F\n``` Java []\nclass Solution {\n public String longestPalindrome(String s) {\n // Check if the input string is empty, return an empty string if so\n if (s.isEmpty())\n return "";\n\n // Initialize variables to store the indices of the longest palindrome found\n int[] longestPalindromeIndices = { 0, 0 };\n\n // Loop through the characters in the input string\n for (int i = 0; i < s.length(); ++i) {\n // Find the indices of the longest palindrome centered at character i\n int[] currentIndices = expandAroundCenter(s, i, i);\n\n // Compare the length of the current palindrome with the longest found so far\n if (currentIndices[1] - currentIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the current one is longer\n longestPalindromeIndices = currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if (i + 1 < s.length() && s.charAt(i) == s.charAt(i + 1)) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n int[] evenIndices = expandAroundCenter(s, i, i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so\n // far\n if (evenIndices[1] - evenIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the even-length one is longer\n longestPalindromeIndices = evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return s.substring(longestPalindromeIndices[0], longestPalindromeIndices[1] + 1);\n }\n\n // Helper function to find and return the indices of the longest palindrome\n // extended from s[i..j] (inclusive) by expanding around the center\n private int[] expandAroundCenter(final String s, int i, int j) {\n // Expand the palindrome by moving outward from the center while the characters\n // match\n while (i >= 0 && j < s.length() && s.charAt(i) == s.charAt(j)) {\n i--; // Move the left index to the left\n j++; // Move the right index to the right\n }\n // Return the indices of the longest palindrome found\n return new int[] { i + 1, j - 1 };\n }\n}\n\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n // Check if the input string is empty, return an empty string if so\n if (s.empty())\n return "";\n\n // Initialize variables to store the indices of the longest palindrome found\n std::vector<int> longestPalindromeIndices = {0, 0};\n\n for (int i = 0; i < s.length(); ++i) {\n // Find the indices of the longest palindrome centered at character i\n std::vector<int> currentIndices = expandAroundCenter(s, i, i);\n\n // Compare the length of the current palindrome with the longest found so far\n if (currentIndices[1] - currentIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n longestPalindromeIndices = currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if (i + 1 < s.length() && s[i] == s[i + 1]) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n std::vector<int> evenIndices = expandAroundCenter(s, i, i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so far\n if (evenIndices[1] - evenIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n longestPalindromeIndices = evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return s.substr(longestPalindromeIndices[0], longestPalindromeIndices[1] - longestPalindromeIndices[0] + 1);\n }\n\nprivate:\n // Helper function to find and return the indices of the longest palindrome\n // extended from s[i..j] (inclusive) by expanding around the center\n std::vector<int> expandAroundCenter(const std::string &s, int i, int j) {\n while (i >= 0 && j < s.length() && s[i] == s[j]) {\n --i;\n ++j;\n }\n return {i + 1, j - 1};\n }\n};\n\n```\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n # Check if the input string is empty, return an empty string if so\n if not s:\n return ""\n\n # Initialize variables to store the indices of the longest palindrome found\n longest_palindrome_indices = [0, 0]\n\n def expand_around_center(s, i, j):\n # Helper function to find and return the indices of the longest palindrome\n # extended from s[i..j] (inclusive) by expanding around the center\n while i >= 0 and j < len(s) and s[i] == s[j]:\n i -= 1\n j += 1\n return [i + 1, j - 1]\n\n for i in range(len(s)):\n current_indices = expand_around_center(s, i, i)\n\n # Compare the length of the current palindrome with the longest found so far\n if current_indices[1] - current_indices[0] > longest_palindrome_indices[1] - longest_palindrome_indices[0]:\n longest_palindrome_indices = current_indices\n\n if i + 1 < len(s) and s[i] == s[i + 1]:\n even_indices = expand_around_center(s, i, i + 1)\n\n # Compare the length of the even-length palindrome with the longest found so far\n if even_indices[1] - even_indices[0] > longest_palindrome_indices[1] - longest_palindrome_indices[0]:\n longest_palindrome_indices = even_indices\n\n # Extract and return the longest palindrome substring using the indices\n return s[longest_palindrome_indices[0]:longest_palindrome_indices[1] + 1]\n\n```\n``` JavaScript []\nvar longestPalindrome = function(s) {\n // Check if the input string is empty, return an empty string if so\n if (s.length === 0)\n return "";\n\n // Initialize variables to store the indices of the longest palindrome found\n let longestPalindromeIndices = [0, 0];\n\n // Loop through the characters in the input string\n for (let i = 0; i < s.length; ++i) {\n // Find the indices of the longest palindrome centered at character i\n let currentIndices = expandAroundCenter(s, i, i);\n\n // Compare the length of the current palindrome with the longest found so far\n if (currentIndices[1] - currentIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the current one is longer\n longestPalindromeIndices = currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if (i + 1 < s.length && s[i] === s[i + 1]) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n let evenIndices = expandAroundCenter(s, i, i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so\n // far\n if (evenIndices[1] - evenIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the even-length one is longer\n longestPalindromeIndices = evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return s.slice(longestPalindromeIndices[0], longestPalindromeIndices[1] + 1);\n}\n\n// Helper function to find and return the indices of the longest palindrome\n// extended from s[i..j] (inclusive) by expanding around the center\nfunction expandAroundCenter(s, i, j) {\n // Expand the palindrome by moving outward from the center while the characters match\n while (i >= 0 && j < s.length && s[i] === s[j]) {\n i--; // Move the left index to the left\n j++; // Move the right index to the right\n }\n // Return the indices of the longest palindrome found\n return [i + 1, j - 1];\n}\n\n```\n``` C# []\npublic class Solution {\n public string LongestPalindrome(string s) {\n // Check if the input string is empty, return an empty string if so\n if (string.IsNullOrEmpty(s))\n return "";\n\n // Initialize variables to store the indices of the longest palindrome found\n int[] longestPalindromeIndices = { 0, 0 };\n\n // Loop through the characters in the input string\n for (int i = 0; i < s.Length; ++i) {\n // Find the indices of the longest palindrome centered at character i\n int[] currentIndices = ExpandAroundCenter(s, i, i);\n\n // Compare the length of the current palindrome with the longest found so far\n if (currentIndices[1] - currentIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the current one is longer\n longestPalindromeIndices = currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if (i + 1 < s.Length && s[i] == s[i + 1]) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n int[] evenIndices = ExpandAroundCenter(s, i, i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so\n // far\n if (evenIndices[1] - evenIndices[0] > longestPalindromeIndices[1] - longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the even-length one is longer\n longestPalindromeIndices = evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return s.Substring(longestPalindromeIndices[0], longestPalindromeIndices[1] - longestPalindromeIndices[0] + 1);\n }\n\n // Helper function to find and return the indices of the longest palindrome\n // extended from s[i..j] (inclusive) by expanding around the center\n private int[] ExpandAroundCenter(string s, int i, int j) {\n // Expand the palindrome by moving outward from the center while the characters match\n while (i >= 0 && j < s.Length && s[i] == s[j]) {\n i--; // Move the left index to the left\n j++; // Move the right index to the right\n }\n // Return the indices of the longest palindrome found\n return new int[] { i + 1, j - 1 };\n }\n}\n```\n``` PHP []\nclass Solution {\n public function longestPalindrome($s) {\n // Check if the input string is empty, return an empty string if so\n if (empty($s)) {\n return "";\n }\n\n // Initialize variables to store the indices of the longest palindrome found\n $longestPalindromeIndices = array(0, 0);\n\n // Loop through the characters in the input string\n for ($i = 0; $i < strlen($s); ++$i) {\n // Find the indices of the longest palindrome centered at character i\n $currentIndices = $this->expandAroundCenter($s, $i, $i);\n\n // Compare the length of the current palindrome with the longest found so far\n if ($currentIndices[1] - $currentIndices[0] > $longestPalindromeIndices[1] - $longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the current one is longer\n $longestPalindromeIndices = $currentIndices;\n }\n\n // Check if there is a possibility of an even-length palindrome centered at\n // character i and i+1\n if ($i + 1 < strlen($s) && $s[$i] == $s[$i + 1]) {\n // Find the indices of the longest even-length palindrome centered at characters\n // i and i+1\n $evenIndices = $this->expandAroundCenter($s, $i, $i + 1);\n\n // Compare the length of the even-length palindrome with the longest found so\n // far\n if ($evenIndices[1] - $evenIndices[0] > $longestPalindromeIndices[1] - $longestPalindromeIndices[0]) {\n // Update the longest palindrome indices if the even-length one is longer\n $longestPalindromeIndices = $evenIndices;\n }\n }\n }\n\n // Extract and return the longest palindrome substring using the indices\n return substr($s, $longestPalindromeIndices[0], $longestPalindromeIndices[1] - $longestPalindromeIndices[0] + 1);\n }\n\n // Helper function to find and return the indices of the longest palindrome\n // extended from s[i..j] (inclusive) by expanding around the center\n private function expandAroundCenter($s, $i, $j) {\n // Expand the palindrome by moving outward from the center while the characters match\n while ($i >= 0 && $j < strlen($s) && $s[$i] == $s[$j]) {\n $i--; // Move the left index to the left\n $j++; // Move the right index to the right\n }\n // Return the indices of the longest palindrome found\n return array($i + 1, $j - 1);\n }\n}\n```\n\n\n---\n\n# 2nd Method :- Manacher\'s Algorithm \uD83D\uDEA9\n\n## Intuition \uD83D\uDE80:\nThe code implements Manacher\'s algorithm, which is designed to find the longest palindromic substring in a given string. The algorithm is an efficient way to tackle this problem and is based on the following key ideas:\n\n1. Utilize symmetry: Palindromes have a property of symmetry, which means their left and right sides are mirror images of each other. Manacher\'s algorithm takes advantage of this property to optimize the process.\n\n2. Avoid redundant computations: The algorithm uses previously computed information to avoid redundant checks, which makes it more efficient than brute force methods.\n\n## Approach \uD83D\uDE80:\n\n1. **Preprocessing**:\n - The input string `s` is preprocessed to create a modified string `T` with special characters (^, #, and dollar ) inserted between each character to simplify palindrome detection.\n\n2. **Initialization**:\n - Initialize variables:\n - `strLength` for the length of the modified string `T`.\n - `palindromeLengths`, an array to store the lengths of palindromes centered at each position in `T`.\n - `center` for the current center of the palindrome being processed.\n - `rightEdge` for the rightmost edge of the palindrome found so far.\n\n3. **Palindrome Detection**:\n - Loop through the modified string `T` to find palindromes centered at each position.\n - Calculate the length of the palindrome at the current position `i` based on previously computed information and expand it if possible. This is done by comparing characters around the current position.\n - Update `center` and `rightEdge` if a longer palindrome is found.\n\n4. **Find the Longest Palindrome**:\n - After processing the entire modified string `T`, identify the longest palindrome by searching the `palindromeLengths` array for the maximum value.\n - Determine the center of this longest palindrome.\n\n5. **Extract the Result**:\n - Use the information about the longest palindrome (center and length) in the modified string `T` to extract the corresponding substring from the original input string `s`.\n\nThe code effectively implements this approach to find and return the longest palindromic substring in the input string `s`. Manacher\'s algorithm is more efficient than naive methods because it takes advantage of the properties of palindromes and avoids redundant comparisons, making it a good choice for solving this problem.\n\n\n## Complexity \uD83D\uDE81\n### \uD83C\uDFF9 Time complexity: O(N)\nThe time complexity of Manacher\'s algorithm is O(N), where N is the length of the input string `s`. This is because the algorithm processes each character of the modified string exactly once (with some constant factor overhead) in a linear pass. The key factor in achieving this efficiency is the "center expansion" technique used to find palindromes, which avoids unnecessary character comparisons. \n\n### \uD83C\uDFF9 Space complexity: O(N)\nThe space complexity of the code is O(N) as well. This is primarily due to the creation of the modified string `T`, which is constructed by adding extra characters, such as \'^\', \'#\', and \'$\', to the original string. The `P` array used to store the lengths of palindromes at each position also has a space complexity of O(N) because it is an array of the same length as the modified string. The other variables used in the algorithm (e.g., `C`, `R`, and loop counters) have constant space requirements and do not significantly contribute to the space complexity.\n\nSo, in terms of both time and space complexity, this code is very efficient for finding the longest palindromic substring in a string.\n\n\n## Code \u2712\uFE0F\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n // Step 1: Preprocess the input string\n StringBuilder processedStr = new StringBuilder("^#");\n for (char c : s.toCharArray()) {\n processedStr.append(c).append("#");\n }\n processedStr.append("$");\n String modifiedString = processedStr.toString();\n\n // Step 2: Initialize variables for the algorithm\n int strLength = modifiedString.length();\n int[] palindromeLengths = new int[strLength];\n int center = 0; // Current center of the palindrome\n int rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for (int i = 1; i < strLength - 1; i++) {\n palindromeLengths[i] = (rightEdge > i) ? Math.min(rightEdge - i, palindromeLengths[2 * center - i]) : 0;\n \n // Expand the palindrome around the current character\n while (modifiedString.charAt(i + 1 + palindromeLengths[i]) == modifiedString.charAt(i - 1 - palindromeLengths[i])) {\n palindromeLengths[i]++;\n }\n \n // Update the rightmost edge and center if necessary\n if (i + palindromeLengths[i] > rightEdge) {\n center = i;\n rightEdge = i + palindromeLengths[i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n int maxLength = 0;\n int maxCenter = 0;\n for (int i = 0; i < strLength; i++) {\n if (palindromeLengths[i] > maxLength) {\n maxLength = palindromeLengths[i];\n maxCenter = i;\n }\n }\n \n // Step 5: Extract the longest palindrome from the modified string\n int start = (maxCenter - maxLength) / 2;\n int end = start + maxLength;\n\n // Return the longest palindrome in the original string\n return s.substring(start, end);\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n // Step 1: Preprocess the input string\n std::string processedStr = "^#";\n for (char c : s) {\n processedStr.push_back(c);\n processedStr.push_back(\'#\');\n }\n processedStr.push_back(\'$\');\n\n // Step 2: Initialize variables for the algorithm\n int strLength = processedStr.length();\n std::vector<int> palindromeLengths(strLength, 0);\n int center = 0; // Current center of the palindrome\n int rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for (int i = 1; i < strLength - 1; i++) {\n palindromeLengths[i] = (rightEdge > i) ? std::min(rightEdge - i, palindromeLengths[2 * center - i]) : 0;\n\n // Expand the palindrome around the current character\n while (processedStr[i + 1 + palindromeLengths[i]] == processedStr[i - 1 - palindromeLengths[i]]) {\n palindromeLengths[i]++;\n }\n\n // Update the rightmost edge and center if necessary\n if (i + palindromeLengths[i] > rightEdge) {\n center = i;\n rightEdge = i + palindromeLengths[i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n int maxLength = 0;\n int maxCenter = 0;\n for (int i = 0; i < strLength; i++) {\n if (palindromeLengths[i] > maxLength) {\n maxLength = palindromeLengths[i];\n maxCenter = i;\n }\n }\n\n // Step 5: Extract the longest palindrome from the modified string\n int start = (maxCenter - maxLength) / 2;\n int end = start + maxLength;\n\n // Return the longest palindrome in the original string\n return s.substr(start, end - start);\n }\n};\n```\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n # Step 1: Preprocess the input string\n processed_str = "^#"\n for c in s:\n processed_str += c + "#"\n processed_str += "$"\n\n # Step 2: Initialize variables for the algorithm\n str_length = len(processed_str)\n palindrome_lengths = [0] * str_length\n center = 0 # Current center of the palindrome\n right_edge = 0 # Rightmost edge of the palindrome\n\n # Step 3: Loop through the modified string to find palindromes\n for i in range(1, str_length - 1):\n palindrome_lengths[i] = min(right_edge - i, palindrome_lengths[2 * center - i]) if right_edge > i else 0\n\n # Expand the palindrome around the current character\n while processed_str[i + 1 + palindrome_lengths[i]] == processed_str[i - 1 - palindrome_lengths[i]]:\n palindrome_lengths[i] += 1\n\n # Update the rightmost edge and center if necessary\n if i + palindrome_lengths[i] > right_edge:\n center = i\n right_edge = i + palindrome_lengths[i]\n\n # Step 4: Find the longest palindrome and its center\n max_length = 0\n max_center = 0\n for i in range(str_length):\n if palindrome_lengths[i] > max_length:\n max_length = palindrome_lengths[i]\n max_center = i\n\n # Step 5: Extract the longest palindrome from the modified string\n start = (max_center - max_length) // 2\n end = start + max_length\n\n # Return the longest palindrome in the original string\n return s[start:end]\n```\n``` JavaScript []\nclass Solution {\n longestPalindrome(s) {\n // Step 1: Preprocess the input string\n let processedStr = "^#";\n for (let i = 0; i < s.length; i++) {\n processedStr += s[i] + "#";\n }\n processedStr += "$";\n let modifiedString = processedStr;\n\n // Step 2: Initialize variables for the algorithm\n let strLength = modifiedString.length;\n let palindromeLengths = new Array(strLength).fill(0);\n let center = 0; // Current center of the palindrome\n let rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for (let i = 1; i < strLength - 1; i++) {\n palindromeLengths[i] = (rightEdge > i) ? Math.min(rightEdge - i, palindromeLengths[2 * center - i]) : 0;\n\n // Expand the palindrome around the current character\n while (modifiedString[i + 1 + palindromeLengths[i]] === modifiedString[i - 1 - palindromeLengths[i]]) {\n palindromeLengths[i]++;\n }\n\n // Update the rightmost edge and center if necessary\n if (i + palindromeLengths[i] > rightEdge) {\n center = i;\n rightEdge = i + palindromeLengths[i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n let maxLength = 0;\n let maxCenter = 0;\n for (let i = 0; i < strLength; i++) {\n if (palindromeLengths[i] > maxLength) {\n maxLength = palindromeLengths[i];\n maxCenter = i;\n }\n }\n\n // Step 5: Extract the longest palindrome from the modified string\n let start = (maxCenter - maxLength) / 2;\n let end = start + maxLength;\n\n // Return the longest palindrome in the original string\n return s.substring(start, end);\n }\n}\n```\n``` C# []\npublic class Solution {\n public string LongestPalindrome(string s) {\n // Step 1: Preprocess the input string\n StringBuilder processedStr = new StringBuilder("^#");\n foreach (char c in s) {\n processedStr.Append(c).Append("#");\n }\n processedStr.Append("$");\n string modifiedString = processedStr.ToString();\n\n // Step 2: Initialize variables for the algorithm\n int strLength = modifiedString.Length;\n int[] palindromeLengths = new int[strLength];\n int center = 0; // Current center of the palindrome\n int rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for (int i = 1; i < strLength - 1; i++) {\n palindromeLengths[i] = (rightEdge > i) ? Math.Min(rightEdge - i, palindromeLengths[2 * center - i]) : 0;\n\n // Expand the palindrome around the current character\n while (modifiedString[i + 1 + palindromeLengths[i]] == modifiedString[i - 1 - palindromeLengths[i]]) {\n palindromeLengths[i]++;\n }\n\n // Update the rightmost edge and center if necessary\n if (i + palindromeLengths[i] > rightEdge) {\n center = i;\n rightEdge = i + palindromeLengths[i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n int maxLength = 0;\n int maxCenter = 0;\n for (int i = 0; i < strLength; i++) {\n if (palindromeLengths[i] > maxLength) {\n maxLength = palindromeLengths[i];\n maxCenter = i;\n }\n }\n\n // Step 5: Extract the longest palindrome from the modified string\n int start = (maxCenter - maxLength) / 2;\n int end = start + maxLength;\n\n // Return the longest palindrome in the original string\n return s.Substring(start, end - start);\n }\n}\n```\n``` PHP []\nclass Solution {\n public function longestPalindrome($s) {\n // Step 1: Preprocess the input string\n $processedStr = "^#";\n for ($i = 0; $i < strlen($s); $i++) {\n $processedStr .= $s[$i] . "#";\n }\n $processedStr .= "$";\n $modifiedString = $processedStr;\n\n // Step 2: Initialize variables for the algorithm\n $strLength = strlen($modifiedString);\n $palindromeLengths = array_fill(0, $strLength, 0);\n $center = 0; // Current center of the palindrome\n $rightEdge = 0; // Rightmost edge of the palindrome\n\n // Step 3: Loop through the modified string to find palindromes\n for ($i = 1; $i < $strLength - 1; $i++) {\n $palindromeLengths[$i] = ($rightEdge > $i) ? min($rightEdge - $i, $palindromeLengths[2 * $center - $i]) : 0;\n\n // Expand the palindrome around the current character\n while ($modifiedString[$i + 1 + $palindromeLengths[$i]] == $modifiedString[$i - 1 - $palindromeLengths[$i]]) {\n $palindromeLengths[$i]++;\n }\n\n // Update the rightmost edge and center if necessary\n if ($i + $palindromeLengths[$i] > $rightEdge) {\n $center = $i;\n $rightEdge = $i + $palindromeLengths[$i];\n }\n }\n\n // Step 4: Find the longest palindrome and its center\n $maxLength = 0;\n $maxCenter = 0;\n for ($i = 0; $i < $strLength; $i++) {\n if ($palindromeLengths[$i] > $maxLength) {\n $maxLength = $palindromeLengths[$i];\n $maxCenter = $i;\n }\n }\n\n // Step 5: Extract the longest palindrome from the modified string\n $start = ($maxCenter - $maxLength) / 2;\n $end = $start + $maxLength;\n\n // Return the longest palindrome in the original string\n return substr($s, $start, $end - $start);\n }\n}\n```\n\n\n# Up Vote Guys\n | 45 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅ 98.55% Manacher's algorithm | longest-palindromic-substring | 1 | 1 | # Intuition\nWhen tackling the problem of finding the longest palindromic substring, one might initially think of generating all possible substrings and checking each for palindromicity. However, this approach is inefficient. A more nuanced understanding would lead us to the realization that for each character in the string, it could potentially be the center of a palindrome. Using this intuition, we can attempt to expand around each character to check for palindromes. But how can we make sure to handle palindromes of both even and odd lengths? This is where Manacher\'s algorithm comes in, transforming the string in a way that we only need to handle palindromes centered around a single character.\n\n## Live Codding & Comments\nhttps://youtu.be/6Bq8j2dhzJc?si=zPnSjdkRaNzo5KMa\n\n# Approach\n\n**Manacher\'s Algorithm** is a powerful technique that allows us to find the longest palindromic substring in a given string in linear time. Here\'s a detailed breakdown of the algorithm\'s approach:\n\n### 1. String Transformation\nWe first transform the original string to simplify the algorithm. This transformation achieves two things:\n- It ensures that every potential center of a palindrome is surrounded by identical characters (`#`), which simplifies the process of expanding around a center.\n- It adds special characters `^` at the beginning and `$` at the end of the string to avoid any boundary checks during the palindrome expansion.\n\nFor instance, the string `"babad"` is transformed into `"^#b#a#b#a#d#$"`.\n\n### 2. Initialization\nWe maintain an array `P` with the same length as the transformed string. Each entry `P[i]` denotes the radius (half-length) of the palindrome centered at position `i`.\n\nWe also introduce two critical pointers:\n- `C`: The center of the palindrome that has the rightmost boundary.\n- `R`: The right boundary of this palindrome.\n\nBoth `C` and `R` start at the beginning of the string.\n\n### 3. Iterating Through the String\nFor every character in the transformed string, we consider it as a potential center for a palindrome.\n\n**a. Using Previously Computed Information**: \nIf the current position is to the left of `R`, its mirror position about the center `C` might have information about a palindrome centered at the current position. We can leverage this to avoid unnecessary calculations.\n\n**b. Expanding Around the Center**: \nStarting from the current radius at position `i` (which might be derived from its mirror or initialized to 0), we attempt to expand around `i` and check if the characters are the same.\n\n**c. Updating `C` and `R`**: \nIf the palindrome centered at `i` extends beyond `R`, we update `C` to `i` and `R` to the new boundary.\n\n### 4. Extracting the Result\nOnce we\'ve computed the palindromic radii for all positions in the transformed string, we find the position with the largest radius in `P`. This position represents the center of the longest palindromic substring. We then extract and return this palindrome from the original string.\n\n# Complexity\n- Time complexity: $O(n)$\nManacher\'s algorithm processes each character in the transformed string once, making the time complexity linear.\n\n- Space complexity: $O(n)$\nWe use an array `P` to store the palindrome radii, making the space complexity linear as well.\n\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n T = \'#\'.join(\'^{}$\'.format(s))\n n = len(T)\n P = [0] * n\n C = R = 0\n \n for i in range(1, n-1):\n P[i] = (R > i) and min(R - i, P[2*C - i])\n while T[i + 1 + P[i]] == T[i - 1 - P[i]]:\n P[i] += 1\n \n if i + P[i] > R:\n C, R = i, i + P[i]\n \n max_len, center_index = max((n, i) for i, n in enumerate(P))\n return s[(center_index - max_len) // 2: (center_index + max_len) // 2]\n```\n``` Go []\nfunc longestPalindrome(s string) string {\n T := "^#" + strings.Join(strings.Split(s, ""), "#") + "#$"\n n := len(T)\n P := make([]int, n)\n C, R := 0, 0\n \n for i := 1; i < n-1; i++ {\n if R > i {\n P[i] = min(R-i, P[2*C-i])\n }\n for T[i+1+P[i]] == T[i-1-P[i]] {\n P[i]++\n }\n if i + P[i] > R {\n C, R = i, i + P[i]\n }\n }\n \n maxLen := 0\n centerIndex := 0\n for i, v := range P {\n if v > maxLen {\n maxLen = v\n centerIndex = i\n }\n }\n return s[(centerIndex-maxLen)/2 : (centerIndex+maxLen)/2]\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n StringBuilder sb = new StringBuilder("^#");\n for (char c : s.toCharArray()) {\n sb.append(c).append("#");\n }\n sb.append("$");\n String T = sb.toString();\n \n int n = T.length();\n int[] P = new int[n];\n int C = 0, R = 0;\n \n for (int i = 1; i < n-1; i++) {\n P[i] = (R > i) ? Math.min(R - i, P[2*C - i]) : 0;\n while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i]))\n P[i]++;\n \n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n }\n \n int max_len = 0, center_index = 0;\n for (int i = 0; i < n; i++) {\n if (P[i] > max_len) {\n max_len = P[i];\n center_index = i;\n }\n }\n return s.substring((center_index - max_len) / 2, (center_index + max_len) / 2);\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n std::string T = "^#";\n for (char c : s) {\n T += c;\n T += \'#\';\n }\n T += "$";\n\n int n = T.size();\n std::vector<int> P(n, 0);\n int C = 0, R = 0;\n\n for (int i = 1; i < n-1; ++i) {\n P[i] = (R > i) ? std::min(R - i, P[2*C - i]) : 0;\n while (T[i + 1 + P[i]] == T[i - 1 - P[i]])\n P[i]++;\n\n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n }\n\n int max_len = *std::max_element(P.begin(), P.end());\n int center_index = std::distance(P.begin(), std::find(P.begin(), P.end(), max_len));\n return s.substr((center_index - max_len) / 2, max_len);\n }\n};\n```\n``` PHP []\nclass Solution {\n function longestPalindrome($s) {\n $T = "^#".implode("#", str_split($s))."#$";\n $n = strlen($T);\n $P = array_fill(0, $n, 0);\n $C = $R = 0;\n \n for ($i = 1; $i < $n-1; $i++) {\n $P[$i] = ($R > $i) ? min($R - $i, $P[2*$C - $i]) : 0;\n while ($T[$i + 1 + $P[$i]] == $T[$i - 1 - $P[$i]])\n $P[$i]++;\n \n if ($i + $P[$i] > $R) {\n $C = $i;\n $R = $i + $P[$i];\n }\n }\n \n $max_len = max($P);\n $center_index = array_search($max_len, $P);\n return substr($s, ($center_index - $max_len) / 2, $max_len);\n }\n}\n```\n``` C# []\npublic class Solution {\n public string LongestPalindrome(string s) {\n string T = "^#" + string.Join("#", s.ToCharArray()) + "#$";\n int n = T.Length;\n int[] P = new int[n];\n int C = 0, R = 0;\n \n for (int i = 1; i < n-1; i++) {\n P[i] = (R > i) ? Math.Min(R - i, P[2*C - i]) : 0;\n while (T[i + 1 + P[i]] == T[i - 1 - P[i]])\n P[i]++;\n \n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n }\n \n int max_len = P.Max();\n int center_index = Array.IndexOf(P, max_len);\n return s.Substring((center_index - max_len) / 2, max_len);\n }\n}\n```\n``` JavaScript []\nvar longestPalindrome = function(s) {\n let T = "^#" + s.split("").join("#") + "#$";\n let n = T.length;\n let P = new Array(n).fill(0);\n let C = 0, R = 0;\n \n for (let i = 1; i < n-1; i++) {\n P[i] = (R > i) ? Math.min(R - i, P[2*C - i]) : 0;\n while (T[i + 1 + P[i]] === T[i - 1 - P[i]])\n P[i]++;\n \n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n }\n \n let max_len = Math.max(...P);\n let center_index = P.indexOf(max_len);\n return s.substring((center_index - max_len) / 2, (center_index + max_len) / 2);\n }\n```\n\n# Performance\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|-------------|\n| Go | 5 | 5.2 |\n| Java | 8 | 43.2 |\n| C++ | 11 | 8.7 |\n| PHP | 18 | 19.4 |\n| C# | 67 | 40.5 |\n| JavaScript | 71 | 45.6 |\n| Python3 | 90 | 16.4 |\n\n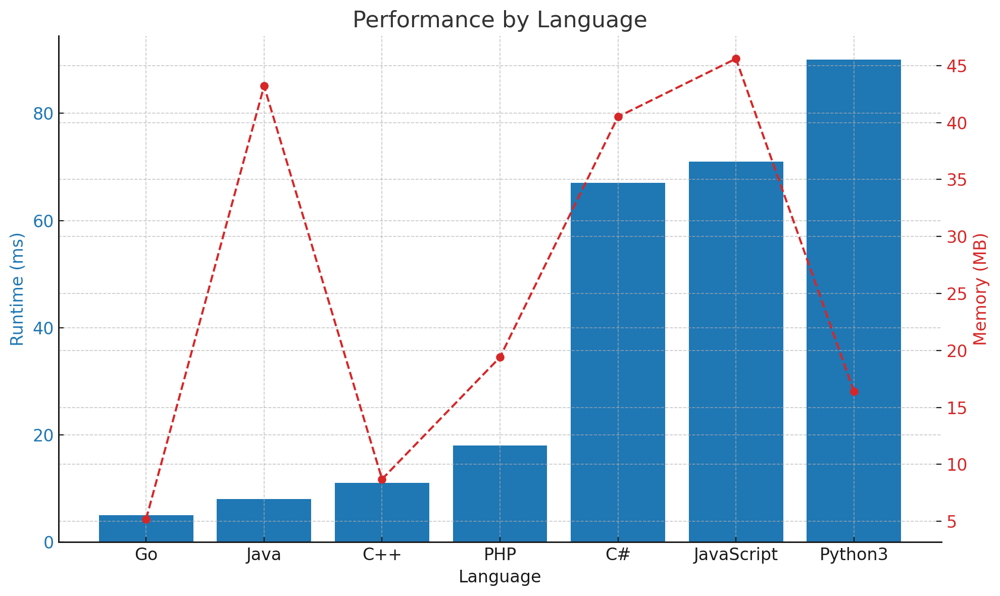\n\n\n# What did we learn?\nWe learned about Manacher\'s algorithm, a linear-time solution to the longest palindromic substring problem. By transforming the string and leveraging the properties of palindromes, we can efficiently determine the longest palindrome without checking every possible substring.\n\n# Why does it work?\nManacher\'s algorithm works by taking advantage of the symmetrical nature of palindromes. It avoids redundant checks by using the information from previously computed palindromes. The transformation of the string ensures that we don\'t need to separately handle even and odd length palindromes.\n\n# What is the optimization here?\nThe brilliance of Manacher\'s algorithm lies in its ability to reduce the problem from quadratic to linear time. By using the palindrome information already computed and the nature of palindromes themselves, the algorithm avoids unnecessary checks, making it one of the most optimal solutions for this problem. | 37 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅ 98.55% Manacher's algorithm | longest-palindromic-substring | 1 | 1 | # Intuition\nWhen tackling the problem of finding the longest palindromic substring, one might initially think of generating all possible substrings and checking each for palindromicity. However, this approach is inefficient. A more nuanced understanding would lead us to the realization that for each character in the string, it could potentially be the center of a palindrome. Using this intuition, we can attempt to expand around each character to check for palindromes. But how can we make sure to handle palindromes of both even and odd lengths? This is where Manacher\'s algorithm comes in, transforming the string in a way that we only need to handle palindromes centered around a single character.\n\n## Live Codding & Comments\nhttps://youtu.be/6Bq8j2dhzJc?si=zPnSjdkRaNzo5KMa\n\n# Approach\n\n**Manacher\'s Algorithm** is a powerful technique that allows us to find the longest palindromic substring in a given string in linear time. Here\'s a detailed breakdown of the algorithm\'s approach:\n\n### 1. String Transformation\nWe first transform the original string to simplify the algorithm. This transformation achieves two things:\n- It ensures that every potential center of a palindrome is surrounded by identical characters (`#`), which simplifies the process of expanding around a center.\n- It adds special characters `^` at the beginning and `$` at the end of the string to avoid any boundary checks during the palindrome expansion.\n\nFor instance, the string `"babad"` is transformed into `"^#b#a#b#a#d#$"`.\n\n### 2. Initialization\nWe maintain an array `P` with the same length as the transformed string. Each entry `P[i]` denotes the radius (half-length) of the palindrome centered at position `i`.\n\nWe also introduce two critical pointers:\n- `C`: The center of the palindrome that has the rightmost boundary.\n- `R`: The right boundary of this palindrome.\n\nBoth `C` and `R` start at the beginning of the string.\n\n### 3. Iterating Through the String\nFor every character in the transformed string, we consider it as a potential center for a palindrome.\n\n**a. Using Previously Computed Information**: \nIf the current position is to the left of `R`, its mirror position about the center `C` might have information about a palindrome centered at the current position. We can leverage this to avoid unnecessary calculations.\n\n**b. Expanding Around the Center**: \nStarting from the current radius at position `i` (which might be derived from its mirror or initialized to 0), we attempt to expand around `i` and check if the characters are the same.\n\n**c. Updating `C` and `R`**: \nIf the palindrome centered at `i` extends beyond `R`, we update `C` to `i` and `R` to the new boundary.\n\n### 4. Extracting the Result\nOnce we\'ve computed the palindromic radii for all positions in the transformed string, we find the position with the largest radius in `P`. This position represents the center of the longest palindromic substring. We then extract and return this palindrome from the original string.\n\n# Complexity\n- Time complexity: $O(n)$\nManacher\'s algorithm processes each character in the transformed string once, making the time complexity linear.\n\n- Space complexity: $O(n)$\nWe use an array `P` to store the palindrome radii, making the space complexity linear as well.\n\n# Code\n``` Python []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n T = \'#\'.join(\'^{}$\'.format(s))\n n = len(T)\n P = [0] * n\n C = R = 0\n \n for i in range(1, n-1):\n P[i] = (R > i) and min(R - i, P[2*C - i])\n while T[i + 1 + P[i]] == T[i - 1 - P[i]]:\n P[i] += 1\n \n if i + P[i] > R:\n C, R = i, i + P[i]\n \n max_len, center_index = max((n, i) for i, n in enumerate(P))\n return s[(center_index - max_len) // 2: (center_index + max_len) // 2]\n```\n``` Go []\nfunc longestPalindrome(s string) string {\n T := "^#" + strings.Join(strings.Split(s, ""), "#") + "#$"\n n := len(T)\n P := make([]int, n)\n C, R := 0, 0\n \n for i := 1; i < n-1; i++ {\n if R > i {\n P[i] = min(R-i, P[2*C-i])\n }\n for T[i+1+P[i]] == T[i-1-P[i]] {\n P[i]++\n }\n if i + P[i] > R {\n C, R = i, i + P[i]\n }\n }\n \n maxLen := 0\n centerIndex := 0\n for i, v := range P {\n if v > maxLen {\n maxLen = v\n centerIndex = i\n }\n }\n return s[(centerIndex-maxLen)/2 : (centerIndex+maxLen)/2]\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n```\n``` Java []\npublic class Solution {\n public String longestPalindrome(String s) {\n StringBuilder sb = new StringBuilder("^#");\n for (char c : s.toCharArray()) {\n sb.append(c).append("#");\n }\n sb.append("$");\n String T = sb.toString();\n \n int n = T.length();\n int[] P = new int[n];\n int C = 0, R = 0;\n \n for (int i = 1; i < n-1; i++) {\n P[i] = (R > i) ? Math.min(R - i, P[2*C - i]) : 0;\n while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i]))\n P[i]++;\n \n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n }\n \n int max_len = 0, center_index = 0;\n for (int i = 0; i < n; i++) {\n if (P[i] > max_len) {\n max_len = P[i];\n center_index = i;\n }\n }\n return s.substring((center_index - max_len) / 2, (center_index + max_len) / 2);\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n std::string T = "^#";\n for (char c : s) {\n T += c;\n T += \'#\';\n }\n T += "$";\n\n int n = T.size();\n std::vector<int> P(n, 0);\n int C = 0, R = 0;\n\n for (int i = 1; i < n-1; ++i) {\n P[i] = (R > i) ? std::min(R - i, P[2*C - i]) : 0;\n while (T[i + 1 + P[i]] == T[i - 1 - P[i]])\n P[i]++;\n\n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n }\n\n int max_len = *std::max_element(P.begin(), P.end());\n int center_index = std::distance(P.begin(), std::find(P.begin(), P.end(), max_len));\n return s.substr((center_index - max_len) / 2, max_len);\n }\n};\n```\n``` PHP []\nclass Solution {\n function longestPalindrome($s) {\n $T = "^#".implode("#", str_split($s))."#$";\n $n = strlen($T);\n $P = array_fill(0, $n, 0);\n $C = $R = 0;\n \n for ($i = 1; $i < $n-1; $i++) {\n $P[$i] = ($R > $i) ? min($R - $i, $P[2*$C - $i]) : 0;\n while ($T[$i + 1 + $P[$i]] == $T[$i - 1 - $P[$i]])\n $P[$i]++;\n \n if ($i + $P[$i] > $R) {\n $C = $i;\n $R = $i + $P[$i];\n }\n }\n \n $max_len = max($P);\n $center_index = array_search($max_len, $P);\n return substr($s, ($center_index - $max_len) / 2, $max_len);\n }\n}\n```\n``` C# []\npublic class Solution {\n public string LongestPalindrome(string s) {\n string T = "^#" + string.Join("#", s.ToCharArray()) + "#$";\n int n = T.Length;\n int[] P = new int[n];\n int C = 0, R = 0;\n \n for (int i = 1; i < n-1; i++) {\n P[i] = (R > i) ? Math.Min(R - i, P[2*C - i]) : 0;\n while (T[i + 1 + P[i]] == T[i - 1 - P[i]])\n P[i]++;\n \n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n }\n \n int max_len = P.Max();\n int center_index = Array.IndexOf(P, max_len);\n return s.Substring((center_index - max_len) / 2, max_len);\n }\n}\n```\n``` JavaScript []\nvar longestPalindrome = function(s) {\n let T = "^#" + s.split("").join("#") + "#$";\n let n = T.length;\n let P = new Array(n).fill(0);\n let C = 0, R = 0;\n \n for (let i = 1; i < n-1; i++) {\n P[i] = (R > i) ? Math.min(R - i, P[2*C - i]) : 0;\n while (T[i + 1 + P[i]] === T[i - 1 - P[i]])\n P[i]++;\n \n if (i + P[i] > R) {\n C = i;\n R = i + P[i];\n }\n }\n \n let max_len = Math.max(...P);\n let center_index = P.indexOf(max_len);\n return s.substring((center_index - max_len) / 2, (center_index + max_len) / 2);\n }\n```\n\n# Performance\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|-------------|\n| Go | 5 | 5.2 |\n| Java | 8 | 43.2 |\n| C++ | 11 | 8.7 |\n| PHP | 18 | 19.4 |\n| C# | 67 | 40.5 |\n| JavaScript | 71 | 45.6 |\n| Python3 | 90 | 16.4 |\n\n\n\n\n# What did we learn?\nWe learned about Manacher\'s algorithm, a linear-time solution to the longest palindromic substring problem. By transforming the string and leveraging the properties of palindromes, we can efficiently determine the longest palindrome without checking every possible substring.\n\n# Why does it work?\nManacher\'s algorithm works by taking advantage of the symmetrical nature of palindromes. It avoids redundant checks by using the information from previously computed palindromes. The transformation of the string ensures that we don\'t need to separately handle even and odd length palindromes.\n\n# What is the optimization here?\nThe brilliance of Manacher\'s algorithm lies in its ability to reduce the problem from quadratic to linear time. By using the palindrome information already computed and the nature of palindromes themselves, the algorithm avoids unnecessary checks, making it one of the most optimal solutions for this problem. | 37 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Python Solution : with detailed explanation : using DP | longest-palindromic-substring | 0 | 1 | #### Approach (implemented Dp rules)\n* ##### Definition : the row and col in the dp table represent the slicing index on the string s (inclusive)\n* ##### example s = \'babad\' -- > dp[2][3] = s[2:3] = ba\n##### Steps : \n* ##### Fill the diagonal with True, b/c every single character by itself is palindrom \n* ##### Don\'t traverse in the bottom part of the diagonal \n\t* ##### Becuase, that represent reverse slicing (which is not valid)\n##### \n* ##### Iterate backward starting from the most right bottom cell to top (only on the right side of the digonal) \n\t* ##### How ? \n\t\t* ##### \t\tStart itertating backward for the outer loop (i) and for the inner loop (j) iterate forward starting from the index of outer loop ) : see the code (the for loops) \n##### \n* ##### - Pick character from the input string based on the at i and j position, If the characters matches : you need to check two conditions\n\t* ##### 1. If the length of the sub_string is just one (a letter matching is good to be a palindrom)\n\t* ##### 2. But if the length of the sub_string is > 1 \n\t\t* ##### - You need to check if the inner sub_sting is also palindrom\n\t\t* ##### - How ?\n\t\t\t* ##### - You go to the left bottom corner and check if it is True \n\t\t\t* ##### - Left bottom corrner represent the inner sub_string of the current_sub_string \n\t\t\t\t* ##### -Eg. if dp[i][j]= cur_sub_string = \'ababa\' --> True because dp[i+1][j-1] is True\n\t\t\t\t* ##### dp[i+1][j-1] = \'bab\' = True\n\t\t\t\t* ##### .Howerver if dp[i][j]= cur_sub_string = \'abaca\' --> False because dp[i+1][j-1] is False\n\t\t\t\t* ##### dp[i+1][j-1] = \'bac\' = False --> not palindrom \n\t\t* ##### \n\t\t* ##### If dp[i+1][j-1] == True:\n\t\t\t* ##### Ok that means the current sub_string is also palindrom \n\t\t* ##### - Now compare the length of the current_palindrom sub_string with the prvious longest one and take the max\n* ##### - Else : the characters don\'t match\n\t* ##### Just pass\n* ##### - Finally return the maximum number in the dp\n* ##### If this solution/explanation helps you, don\'t forget to upvote as appreciation\n\n```\ndef longestPalindrome(self, s):\n longest_palindrom = \'\'\n dp = [[0]*len(s) for _ in range(len(s))]\n #filling out the diagonal by 1\n for i in range(len(s)):\n dp[i][i] = True\n longest_palindrom = s[i]\n\t\t\t\n # filling the dp table\n for i in range(len(s)-1,-1,-1):\n\t\t\t\t# j starts from the i location : to only work on the upper side of the diagonal \n for j in range(i+1,len(s)): \n if s[i] == s[j]: #if the chars mathces\n # if len slicied sub_string is just one letter if the characters are equal, we can say they are palindomr dp[i][j] =True \n #if the slicied sub_string is longer than 1, then we should check if the inner string is also palindrom (check dp[i+1][j-1] is True)\n if j-i ==1 or dp[i+1][j-1] is True:\n dp[i][j] = True\n # we also need to keep track of the maximum palindrom sequence \n if len(longest_palindrom) < len(s[i:j+1]):\n longest_palindrom = s[i:j+1]\n \n return longest_palindrom\n``` | 722 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Python Solution : with detailed explanation : using DP | longest-palindromic-substring | 0 | 1 | #### Approach (implemented Dp rules)\n* ##### Definition : the row and col in the dp table represent the slicing index on the string s (inclusive)\n* ##### example s = \'babad\' -- > dp[2][3] = s[2:3] = ba\n##### Steps : \n* ##### Fill the diagonal with True, b/c every single character by itself is palindrom \n* ##### Don\'t traverse in the bottom part of the diagonal \n\t* ##### Becuase, that represent reverse slicing (which is not valid)\n##### \n* ##### Iterate backward starting from the most right bottom cell to top (only on the right side of the digonal) \n\t* ##### How ? \n\t\t* ##### \t\tStart itertating backward for the outer loop (i) and for the inner loop (j) iterate forward starting from the index of outer loop ) : see the code (the for loops) \n##### \n* ##### - Pick character from the input string based on the at i and j position, If the characters matches : you need to check two conditions\n\t* ##### 1. If the length of the sub_string is just one (a letter matching is good to be a palindrom)\n\t* ##### 2. But if the length of the sub_string is > 1 \n\t\t* ##### - You need to check if the inner sub_sting is also palindrom\n\t\t* ##### - How ?\n\t\t\t* ##### - You go to the left bottom corner and check if it is True \n\t\t\t* ##### - Left bottom corrner represent the inner sub_string of the current_sub_string \n\t\t\t\t* ##### -Eg. if dp[i][j]= cur_sub_string = \'ababa\' --> True because dp[i+1][j-1] is True\n\t\t\t\t* ##### dp[i+1][j-1] = \'bab\' = True\n\t\t\t\t* ##### .Howerver if dp[i][j]= cur_sub_string = \'abaca\' --> False because dp[i+1][j-1] is False\n\t\t\t\t* ##### dp[i+1][j-1] = \'bac\' = False --> not palindrom \n\t\t* ##### \n\t\t* ##### If dp[i+1][j-1] == True:\n\t\t\t* ##### Ok that means the current sub_string is also palindrom \n\t\t* ##### - Now compare the length of the current_palindrom sub_string with the prvious longest one and take the max\n* ##### - Else : the characters don\'t match\n\t* ##### Just pass\n* ##### - Finally return the maximum number in the dp\n* ##### If this solution/explanation helps you, don\'t forget to upvote as appreciation\n\n```\ndef longestPalindrome(self, s):\n longest_palindrom = \'\'\n dp = [[0]*len(s) for _ in range(len(s))]\n #filling out the diagonal by 1\n for i in range(len(s)):\n dp[i][i] = True\n longest_palindrom = s[i]\n\t\t\t\n # filling the dp table\n for i in range(len(s)-1,-1,-1):\n\t\t\t\t# j starts from the i location : to only work on the upper side of the diagonal \n for j in range(i+1,len(s)): \n if s[i] == s[j]: #if the chars mathces\n # if len slicied sub_string is just one letter if the characters are equal, we can say they are palindomr dp[i][j] =True \n #if the slicied sub_string is longer than 1, then we should check if the inner string is also palindrom (check dp[i+1][j-1] is True)\n if j-i ==1 or dp[i+1][j-1] is True:\n dp[i][j] = True\n # we also need to keep track of the maximum palindrom sequence \n if len(longest_palindrom) < len(s[i:j+1]):\n longest_palindrom = s[i:j+1]\n \n return longest_palindrom\n``` | 722 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
🔥🚀Beats 99.90%🚀 | 🔥🚩Optimised Code | 🧭O(n^2) Time & O(1) Space |🔥 Using Dynamic Programming🔥 | longest-palindromic-substring | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe given code is an implementation of the "Expand Around Center" approach for finding the longest palindromic substring in a given string. This approach works by iterating through each character in the string and expanding around it to check for palindromes. It takes advantage of the fact that a palindrome can be centered around a single character (in the case of odd-length palindromes) or between two characters (in the case of even-length palindromes). By expanding from each character, it identifies the longest palindrome.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The `expandAroundCenter` function takes a string `s` and two indices `left` and `right`. It starts from the characters at these indices and expands outwards while checking if the characters are the same. When different characters are encountered, the function returns the substring between `left` and `right`, which is a palindrome.\n\n2. The `longestPalindrome` function initializes an empty string longest to keep track of the `longest` palindromic substring found.\n\n3. It iterates through the characters of the input string s. For each character, it calls `expandAroundCenter` twice, once assuming an odd-length palindrome (with the character as the center) and once assuming an even-length palindrome (with the character and the next character as the center).\n\n4. If the length of the palindrome found (either odd or even) is greater than the length of the `longest` palindrome found so far, it updates the `longest` substring.\n\n5. After iterating through all characters, it returns the longest palindromic substring found.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this code is O(n^2), where \'n\' is the length of the input string \'s\'. This is because, in the worst case, for each of the \'n\' characters in \'s\', we may expand to both the left and the right, resulting in a quadratic time complexity.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this code is O(1) because it doesn\'t use any additional data structures that grow with the input size. The space is primarily used for the variables and temporary substrings, which don\'t depend on the input size.\n\n---\n\n# \uD83D\uDCA1If you have come this far, then i would like to request you to please upvote this solution\u2763\uFE0F\uD83D\uDCA1So that it could reach out to another one\uD83D\uDD25\uD83D\uDD25\n\n---\n\n```C++ []\n#include <iostream>\nusing namespace std;\n\nclass Solution {\npublic:\nstring expandAroundCenter(string s, int left, int right) {\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n return s.substr(left + 1, right - left - 1);\n}\n\nstring longestPalindrome(string s) {\n string longest = "";\n for (int i = 0; i < s.length(); i++) {\n string odd = expandAroundCenter(s, i, i);\n string even = expandAroundCenter(s, i, i + 1);\n if (odd.length() > longest.length()) longest = odd;\n if (even.length() > longest.length()) longest = even;\n }\n return longest;\n}\n};\n```\n```Java []\npublic class Solution {\n public String expandAroundCenter(String s, int left, int right) {\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n left--;\n right++;\n }\n return s.substring(left + 1, right);\n }\n\n public String longestPalindrome(String s) {\n String longest = "";\n for (int i = 0; i < s.length(); i++) {\n String odd = expandAroundCenter(s, i, i);\n String even = expandAroundCenter(s, i, i + 1);\n if (odd.length() > longest.length()) {\n longest = odd;\n }\n if (even.length() > longest.length()) {\n longest = even;\n }\n }\n return longest;\n }\n\n public static void main(String[] args) {\n Solution solution = new Solution();\n String s = "babad";\n String result = solution.longestPalindrome(s);\n System.out.println("Longest Palindromic Substring: " + result);\n }\n}\n\n```\n```Python []\nclass Solution:\n def expandAroundCenter(self, s, left, right):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return s[left + 1:right]\n\n def longestPalindrome(self, s):\n longest = ""\n for i in range(len(s)):\n odd = self.expandAroundCenter(s, i, i)\n even = self.expandAroundCenter(s, i, i + 1)\n if len(odd) > len(longest):\n longest = odd\n if len(even) > len(longest):\n longest = even\n return longest\n\nsolution = Solution()\ns = "babad"\nresult = solution.longestPalindrome(s)\nprint("Longest Palindromic Substring:", result)\n\n```\n```Javascript []\n/**\n * @param {string} s\n * @return {string}\n */\nvar longestPalindrome = function(s) {\n function expandAroundCenter(left, right) {\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n left--;\n right++;\n }\n return s.substring(left + 1, right);\n }\n\n let longest = "";\n\n for (let i = 0; i < s.length; i++) {\n let odd = expandAroundCenter(i, i);\n let even = expandAroundCenter(i, i + 1);\n\n if (odd.length > longest.length) {\n longest = odd;\n }\n\n if (even.length > longest.length) {\n longest = even;\n }\n }\n\n return longest;\n};\n\n// Example usage\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log("Longest Palindromic Substring: " + result);\n\n```\n```Ruby []\n# @param {String} s\n# @return {String}\ndef longest_palindrome(s)\n def expand_around_center(s, left, right)\n while left >= 0 && right < s.length && s[left] == s[right]\n left -= 1\n right += 1\n end\n s[left + 1...right]\n end\n\n longest = ""\n\n (0...s.length).each do |i|\n odd = expand_around_center(s, i, i)\n even = expand_around_center(s, i, i + 1)\n\n if odd.length > longest.length\n longest = odd\n end\n\n if even.length > longest.length\n longest = even\n end\n end\n\n return longest\nend\n\n# Example usage\ns = "babad"\nresult = longest_palindrome(s)\nputs "Longest Palindromic Substring: #{result}"\n\n```\n```Typescript []\nfunction longestPalindrome(s: string): string {\n function expandAroundCenter(left: number, right: number): string {\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n left--;\n right++;\n }\n return s.substring(left + 1, right);\n }\n\n let longest = "";\n\n for (let i = 0; i < s.length; i++) {\n let odd = expandAroundCenter(i, i);\n let even = expandAroundCenter(i, i + 1);\n\n if (odd.length > longest.length) {\n longest = odd;\n }\n\n if (even.length > longest.length) {\n longest = even;\n }\n }\n\n return longest;\n}\n\n// Example usage\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log("Longest Palindromic Substring: " + result);\n\n``` | 20 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
🔥🚀Beats 99.90%🚀 | 🔥🚩Optimised Code | 🧭O(n^2) Time & O(1) Space |🔥 Using Dynamic Programming🔥 | longest-palindromic-substring | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe given code is an implementation of the "Expand Around Center" approach for finding the longest palindromic substring in a given string. This approach works by iterating through each character in the string and expanding around it to check for palindromes. It takes advantage of the fact that a palindrome can be centered around a single character (in the case of odd-length palindromes) or between two characters (in the case of even-length palindromes). By expanding from each character, it identifies the longest palindrome.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The `expandAroundCenter` function takes a string `s` and two indices `left` and `right`. It starts from the characters at these indices and expands outwards while checking if the characters are the same. When different characters are encountered, the function returns the substring between `left` and `right`, which is a palindrome.\n\n2. The `longestPalindrome` function initializes an empty string longest to keep track of the `longest` palindromic substring found.\n\n3. It iterates through the characters of the input string s. For each character, it calls `expandAroundCenter` twice, once assuming an odd-length palindrome (with the character as the center) and once assuming an even-length palindrome (with the character and the next character as the center).\n\n4. If the length of the palindrome found (either odd or even) is greater than the length of the `longest` palindrome found so far, it updates the `longest` substring.\n\n5. After iterating through all characters, it returns the longest palindromic substring found.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this code is O(n^2), where \'n\' is the length of the input string \'s\'. This is because, in the worst case, for each of the \'n\' characters in \'s\', we may expand to both the left and the right, resulting in a quadratic time complexity.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this code is O(1) because it doesn\'t use any additional data structures that grow with the input size. The space is primarily used for the variables and temporary substrings, which don\'t depend on the input size.\n\n---\n\n# \uD83D\uDCA1If you have come this far, then i would like to request you to please upvote this solution\u2763\uFE0F\uD83D\uDCA1So that it could reach out to another one\uD83D\uDD25\uD83D\uDD25\n\n---\n\n```C++ []\n#include <iostream>\nusing namespace std;\n\nclass Solution {\npublic:\nstring expandAroundCenter(string s, int left, int right) {\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n return s.substr(left + 1, right - left - 1);\n}\n\nstring longestPalindrome(string s) {\n string longest = "";\n for (int i = 0; i < s.length(); i++) {\n string odd = expandAroundCenter(s, i, i);\n string even = expandAroundCenter(s, i, i + 1);\n if (odd.length() > longest.length()) longest = odd;\n if (even.length() > longest.length()) longest = even;\n }\n return longest;\n}\n};\n```\n```Java []\npublic class Solution {\n public String expandAroundCenter(String s, int left, int right) {\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n left--;\n right++;\n }\n return s.substring(left + 1, right);\n }\n\n public String longestPalindrome(String s) {\n String longest = "";\n for (int i = 0; i < s.length(); i++) {\n String odd = expandAroundCenter(s, i, i);\n String even = expandAroundCenter(s, i, i + 1);\n if (odd.length() > longest.length()) {\n longest = odd;\n }\n if (even.length() > longest.length()) {\n longest = even;\n }\n }\n return longest;\n }\n\n public static void main(String[] args) {\n Solution solution = new Solution();\n String s = "babad";\n String result = solution.longestPalindrome(s);\n System.out.println("Longest Palindromic Substring: " + result);\n }\n}\n\n```\n```Python []\nclass Solution:\n def expandAroundCenter(self, s, left, right):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return s[left + 1:right]\n\n def longestPalindrome(self, s):\n longest = ""\n for i in range(len(s)):\n odd = self.expandAroundCenter(s, i, i)\n even = self.expandAroundCenter(s, i, i + 1)\n if len(odd) > len(longest):\n longest = odd\n if len(even) > len(longest):\n longest = even\n return longest\n\nsolution = Solution()\ns = "babad"\nresult = solution.longestPalindrome(s)\nprint("Longest Palindromic Substring:", result)\n\n```\n```Javascript []\n/**\n * @param {string} s\n * @return {string}\n */\nvar longestPalindrome = function(s) {\n function expandAroundCenter(left, right) {\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n left--;\n right++;\n }\n return s.substring(left + 1, right);\n }\n\n let longest = "";\n\n for (let i = 0; i < s.length; i++) {\n let odd = expandAroundCenter(i, i);\n let even = expandAroundCenter(i, i + 1);\n\n if (odd.length > longest.length) {\n longest = odd;\n }\n\n if (even.length > longest.length) {\n longest = even;\n }\n }\n\n return longest;\n};\n\n// Example usage\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log("Longest Palindromic Substring: " + result);\n\n```\n```Ruby []\n# @param {String} s\n# @return {String}\ndef longest_palindrome(s)\n def expand_around_center(s, left, right)\n while left >= 0 && right < s.length && s[left] == s[right]\n left -= 1\n right += 1\n end\n s[left + 1...right]\n end\n\n longest = ""\n\n (0...s.length).each do |i|\n odd = expand_around_center(s, i, i)\n even = expand_around_center(s, i, i + 1)\n\n if odd.length > longest.length\n longest = odd\n end\n\n if even.length > longest.length\n longest = even\n end\n end\n\n return longest\nend\n\n# Example usage\ns = "babad"\nresult = longest_palindrome(s)\nputs "Longest Palindromic Substring: #{result}"\n\n```\n```Typescript []\nfunction longestPalindrome(s: string): string {\n function expandAroundCenter(left: number, right: number): string {\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n left--;\n right++;\n }\n return s.substring(left + 1, right);\n }\n\n let longest = "";\n\n for (let i = 0; i < s.length; i++) {\n let odd = expandAroundCenter(i, i);\n let even = expandAroundCenter(i, i + 1);\n\n if (odd.length > longest.length) {\n longest = odd;\n }\n\n if (even.length > longest.length) {\n longest = even;\n }\n }\n\n return longest;\n}\n\n// Example usage\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log("Longest Palindromic Substring: " + result);\n\n``` | 20 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
"Expand Around Center" Approach to Finding the Longest Palindromic Substring. | longest-palindromic-substring | 0 | 1 | # **Intuition**\nWe can use the "Expand Around Center" approach to find the longest palindromic substring. \n\nThe idea is to treat each character as a potential center of a palindrome and expand outwards while checking if the characters on both sides match. \n\n---\n\n## **Approach**\n1. Initialize variables to keep track of the start index and maximum length of the palindrome.\n2. Iterate through each character in the string.\n3. For each character, consider it as a potential center for both odd and even-length palindromes.\n4. Expand around the center and check if the characters on both sides match.\n5. Update the start index and maximum length if a longer palindrome is found.\n6. Return the longest palindromic substring based on the start index and maximum length.\n\n---\n\n## **Complexity**\n- **Time complexity**:\n$$O(n^2)$$ in the worst case, where $$n$$ is the length of the input string. This is because for each character, we may need to expand up to $$n/2$$ positions.\n\n\n- **Space complexity**: \n$$O(1)$$, as we use only a constant amount of extra space.\n\n---\n\n# **Code**\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if not s:\n return ""\n\n def expand_around_center(left, right):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return s[left + 1:right]\n\n start = 0\n max_length = 0\n\n for i in range(len(s)):\n # Check for odd-length palindromes\n palindrome1 = expand_around_center(i, i)\n if len(palindrome1) > max_length:\n max_length = len(palindrome1)\n start = i - len(palindrome1) // 2\n\n # Check for even-length palindromes\n palindrome2 = expand_around_center(i, i + 1)\n if len(palindrome2) > max_length:\n max_length = len(palindrome2)\n start = i - len(palindrome2) // 2 + 1\n\n return s[start:start + max_length]\n \n``` | 2 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
"Expand Around Center" Approach to Finding the Longest Palindromic Substring. | longest-palindromic-substring | 0 | 1 | # **Intuition**\nWe can use the "Expand Around Center" approach to find the longest palindromic substring. \n\nThe idea is to treat each character as a potential center of a palindrome and expand outwards while checking if the characters on both sides match. \n\n---\n\n## **Approach**\n1. Initialize variables to keep track of the start index and maximum length of the palindrome.\n2. Iterate through each character in the string.\n3. For each character, consider it as a potential center for both odd and even-length palindromes.\n4. Expand around the center and check if the characters on both sides match.\n5. Update the start index and maximum length if a longer palindrome is found.\n6. Return the longest palindromic substring based on the start index and maximum length.\n\n---\n\n## **Complexity**\n- **Time complexity**:\n$$O(n^2)$$ in the worst case, where $$n$$ is the length of the input string. This is because for each character, we may need to expand up to $$n/2$$ positions.\n\n\n- **Space complexity**: \n$$O(1)$$, as we use only a constant amount of extra space.\n\n---\n\n# **Code**\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if not s:\n return ""\n\n def expand_around_center(left, right):\n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n return s[left + 1:right]\n\n start = 0\n max_length = 0\n\n for i in range(len(s)):\n # Check for odd-length palindromes\n palindrome1 = expand_around_center(i, i)\n if len(palindrome1) > max_length:\n max_length = len(palindrome1)\n start = i - len(palindrome1) // 2\n\n # Check for even-length palindromes\n palindrome2 = expand_around_center(i, i + 1)\n if len(palindrome2) > max_length:\n max_length = len(palindrome2)\n start = i - len(palindrome2) // 2 + 1\n\n return s[start:start + max_length]\n \n``` | 2 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅Unlocking Palindromic Mastery: Leetcode Algorithmic Gems ✅3 Solution💡Beginner's Guide by Mr.Robot | longest-palindromic-substring | 1 | 1 | ### Welcome to the Blog you need to be a Pro-bro in this Problem\n---\n## \uD83D\uDCA1Approach 1: Middle Expansion - Explained in Depth\n\n### \u2728Explanation\nThe Middle Expansion approach is an intuitive method for finding the longest palindromic substring. The idea is to consider each character in the string as a potential center of a palindrome and expand outward to identify the longest palindrome. This method is effective for handling both odd and even-length palindromes.\n\n### \uD83D\uDCDDDetailed Explanation\n1. **Selecting the Center:**\n - Begin by iterating through each character in the string.\n - For each character, consider it as the potential center of a palindrome.\n\n2. **Expanding Outward:**\n - Expand outward from the center to identify palindromes.\n - For odd-length palindromes, expand in both directions.\n - For even-length palindromes, expand around the center two characters.\n\n3. **Updating Longest Palindrome:**\n - Keep track of the start and end indices of the longest palindrome found so far.\n\n### \uD83D\uDCDDDry Run\nLet\'s illustrate the Middle Expansion approach with the input "babad":\n- For \'b\', the expansion yields "b" (odd length).\n- For \'a\', the expansion yields "aba" (odd length).\n- For \'b\', the expansion yields "bab" (even length).\n- For \'a\', the expansion yields "a" (odd length).\n- For \'d\', the expansion yields "d" (odd length).\n\n### \uD83D\uDD0DEdge Cases\nThe Middle Expansion approach handles various edge cases:\n- **Single-Character String:**\n - In this case, each character is considered a palindrome by itself.\n- **Empty String:**\n - The algorithm gracefully handles an empty string, resulting in an empty palindrome.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- **Time Complexity:** O(n\xB2) - In the worst case, each character might be the center, and we expand on both sides.\n- **Space Complexity:** O(1) - We use constant space for variables.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCode \n\n```cpp []\nclass Solution{\nstring longestPalindrome(string s) {\n int start = 0;\n int resLen = 0;\n for(int i = 0; i < s.length(); i++) {\n // Odd length palindrome\n int left = i, right = i;\n while(left >= 0 && right < s.length() && s[left] == s[right]) {\n if(right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n \n // Even length palindrome\n left = i, right = i + 1;\n while(left >= 0 && right < s.length() && s[left] == s[right]) {\n if(right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n }\n return s.substr(start, resLen);\n}\n};\n```\n\n\n```java []\npublic class Solution {\n public String longestPalindrome(String s) {\n int start = 0;\n int resLen = 0;\n for (int i = 0; i < s.length(); i++) {\n // Odd length palindrome\n int left = i, right = i;\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n\n // Even length palindrome\n left = i;\n right = i + 1;\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n }\n return s.substring(start, start + resLen);\n }\n}\n```\n\n```python []\nclass Solution: \n def longestPalindrome(self,s:str):\n start = 0\n res_len = 0\n for i in range(len(s)):\n # Odd length palindrome\n left, right = i, i\n while left >= 0 and right < len(s) and s[left] == s[right]:\n if right - left + 1 > res_len:\n start = left\n res_len = right - left + 1\n left -= 1\n right += 1\n\n # Even length palindrome\n left, right = i, i + 1\n while left >= 0 and right < len(s) and s[left] == s[right]:\n if right - left + 1 > res_len:\n start = left\n res_len = right - left + 1\n left -= 1\n right += 1\n return s[start:start + res_len]\n```\n\n```csharp []\npublic class Solution {\n public string LongestPalindrome(string s) {\n int start = 0;\n int resLen = 0;\n for (int i = 0; i < s.Length; i++) {\n // Odd length palindrome\n int left = i, right = i;\n while (left >= 0 && right < s.Length && s[left] == s[right]) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n\n // Even length palindrome\n left = i;\n right = i + 1;\n while (left >= 0 && right < s.Length && s[left] == s[right]) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n }\n return s.Substring(start, resLen);\n }\n}\n```\n\n```javascript []\nvar longestPalindrome = function(s) {\n let start = 0;\n let resLen = 0;\n for (let i = 0; i < s.length; i++) {\n // Odd length palindrome\n let left = i, right = i;\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n\n // Even length palindrome\n left = i;\n right = i + 1;\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n }\n return s.substring(start, start + resLen);\n};\n```\n---\n\n## \uD83D\uDCCA Analysis\n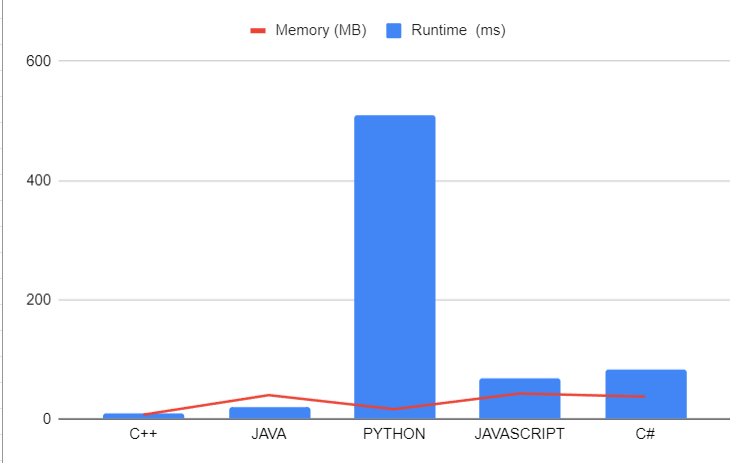\n\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|--------------|\n| C++ | 10 | 7.26 |\n| JAVA | 20 | 40 |\n| PYTHON | 509 | 16.38 |\n| JAVASCRIPT | 68 | 42.72 |\n| C# | 82 | 37.48 |\n\n---\n\n---\n\n## \uD83D\uDCA1Approach 2: Dynamic Programming - Explained in Depth\n\n### \u2728Explanation\nDynamic Programming (DP) is a powerful technique that breaks down a problem into smaller subproblems and solves each subproblem only once, storing the results to avoid redundant computations. In the context of finding the longest palindromic substring, we can use dynamic programming to efficiently check and store information about palindromes.\n\n### \uD83D\uDCDDDetailed Explanation\n1. **Initialization:**\n - Initialize a 2D array, `dp`, where `dp[i][j]` will represent whether the substring from index `i` to `j` is a palindrome.\n - Set the diagonal elements and adjacent two-character substrings initially, as they are trivially palindromes.\n\n2. **Fill the DP Table:**\n - Iterate through the array, starting with larger substrings.\n - For each substring, check if the characters at both ends are equal and if the inner substring is a palindrome (lookup in the DP table).\n\n3. **Maintain Longest Palindrome:**\n - Update the start and end indices of the longest palindromic substring found so far.\n\n### \uD83D\uDCDDDry Run\nLet\'s apply dynamic programming to the input "babad":\n- The table is initialized based on single characters and two-character substrings.\n- For longer substrings, we check if the inner substring is a palindrome and the characters at the ends match.\n\n### \uD83D\uDD0DEdge Cases\nDynamic Programming handles various edge cases:\n- **Single-Character String:**\n - In this case, each character is considered a palindrome by itself.\n- **Empty String:**\n - The algorithm gracefully handles an empty string, resulting in an empty palindrome.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- **Time Complexity:** O(n\xB2) - Filling the table takes quadratic time.\n- **Space Complexity:** O(n\xB2) - We use a 2D array to store information about the palindromic nature of substrings.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCode \n\n```cpp []\nclass Solution {\npublic:\n string longestPalindrome(string s) {\n int size = s.size();\n vector<vector<bool>> dp(size, vector<bool>(size));\n int start = 0, maxLen = 1;\n\n // Initialize for single characters\n for (int i = 0; i < size; i++) {\n dp[i][i] = true;\n }\n\n // Check for two-character substrings\n for (int i = 0; i < size - 1; i++) {\n if (s[i] == s[i + 1]) {\n dp[i][i + 1] = true;\n start = i;\n maxLen = 2;\n }\n }\n\n // Fill the rest of the table\n for (int col = 2; col < size; col++) {\n for (int row = 0; row < size - col; row++) {\n int cl = row + col;\n if (s[row] == s[cl] && dp[row + 1][cl - 1]) {\n dp[row][cl] = true;\n if (col + 1 > maxLen) {\n start = row;\n maxLen = col + 1;\n }\n }\n }\n }\n return s.substr(start, maxLen);\n}\n};\n```\n\n```java []\npublic class Solution {\n public String longestPalindrome(String s) {\n int size = s.length();\n boolean[][] dp = new boolean[size][size];\n int start = 0, maxLen = 1;\n\n // Initialize for single characters\n for (int i = 0; i < size; i++) {\n dp[i][i] = true;\n }\n\n // Check for two-character substrings\n for (int i = 0; i < size - 1; i++) {\n if (s.charAt(i) == s.charAt(i + 1)) {\n dp[i][i + 1] = true;\n start = i;\n maxLen = 2;\n }\n }\n\n // Fill the rest of the table\n for (int col = 2; col < size; col++) {\n for (int row = 0; row < size - col; row++) {\n int cl = row + col;\n if (s.charAt(row) == s.charAt(cl) && dp[row + 1][cl - 1]) {\n dp[row][cl] = true;\n if (col + 1 > maxLen) {\n start = row;\n maxLen = col + 1;\n }\n }\n }\n }\n return s.substring(start, start + maxLen);\n }\n}\n```\n\n```python []\nclass Solution:\n def longestPalindrome(self,s):\n size = len(s)\n dp = [[False] * size for _ in range(size)]\n start = 0\n max_len = 1\n\n # Initialize for single characters\n for i in range(size):\n dp[i][i] = True\n\n # Check for two-character substrings\n for i in range(size - 1):\n if s[i] == s[i + 1]:\n dp[i][i + 1] = True\n start = i\n max_len = 2\n\n # Fill the rest of the table\n for col in range(2, size):\n for row in range(size - col):\n cl = row + col\n if s[row] == s[cl] and dp[row + 1][cl - 1]:\n dp[row][cl] = True\n if col + 1 > max_len:\n start = row\n max_len = col + 1\n\n return s[start:start + max_len]\n```\n\n```csharp []\npublic class Solution {\n public string LongestPalindrome(string s) {\n int size = s.Length;\n bool[,] dp = new bool[size, size];\n int start = 0, maxLen = 1;\n\n // Initialize for single characters\n for (int i = 0; i < size; i++) {\n dp[i, i] = true;\n }\n\n // Check for two-character substrings\n for (int i = 0; i < size - 1; i++) {\n if (s[i] == s[i + 1]) {\n dp[i, i + 1] = true;\n start = i;\n maxLen = 2;\n }\n }\n\n // Fill the rest of the table\n for (int col = 2; col < size; col++) {\n for (int row = 0; row < size - col; row++) {\n int cl = row + col;\n if (s[row] == s[cl] && dp[row + 1, cl - 1]) {\n dp[row, cl] = true;\n if (col + 1 > maxLen) {\n start = row;\n maxLen = col + 1;\n }\n }\n }\n }\n return s.Substring(start, maxLen);\n }\n}\n```\n\n```javascript []\nvar longestPalindrome = function(s) {\n let size = s.length;\n let dp = Array.from(Array(size), () => Array(size).fill(false));\n let start = 0, maxLen = 1;\n\n // Initialize for single characters\n for (let i = 0; i < size; i++) {\n dp[i][i] = true;\n }\n\n // Check for two-character substrings\n for (let i = 0; i < size - 1; i++) {\n if (s[i] === s[i + 1]) {\n dp[i][i + 1] = true;\n start = i;\n maxLen = 2;\n }\n }\n\n // Fill the rest of the table\n for (let col = 2; col < size; col++) {\n for (let row = 0; row < size - col; row++) {\n let cl = row + col;\n if (s[row] === s[cl] && dp[row + 1][cl - 1]) {\n dp[row][cl] = true;\n if (col + 1 > maxLen) {\n start = row;\n maxLen = col + 1;\n }\n }\n }\n }\n return s.substring(start, start + maxLen);\n};\n```\n\n\n---\n\n## \uD83D\uDCCA Analysis\n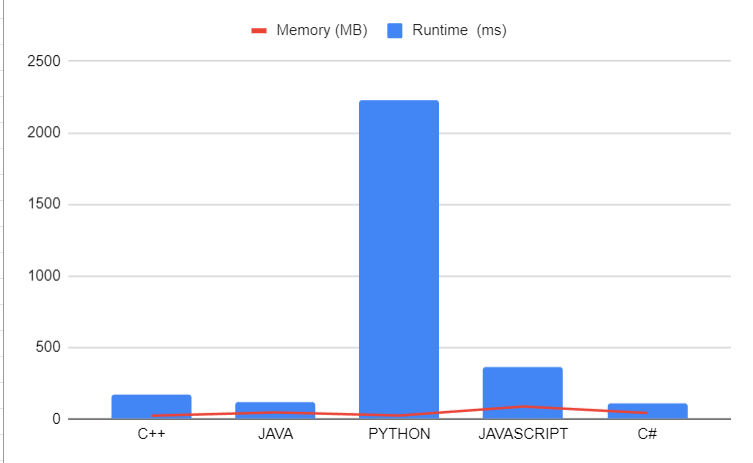\n\n\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|--------------|\n| C++ | 169 | 23 |\n| JAVA | 119 | 45.65 |\n| PYTHON | 2231 | 24.28 |\n| JAVASCRIPT | 364 | 87.11 |\n| C# | 110 | 42 |\n\n\n---\n\n\n---\n\n## \uD83D\uDCA1Approach 3: Manacher\'s Algorithm - A Detailed Exploration\n\n### \u2728Introduction\nManacher\'s Algorithm is a groundbreaking technique designed to find the longest palindromic substring in linear time, making it significantly more efficient than traditional methods. It takes advantage of the inherent symmetry in palindromes to optimize the search process.\n\n### \uD83D\uDCDDDetailed Explanation\n\n#### 1. **Transform the String:**\n - Manacher\'s Algorithm starts by transforming the input string to efficiently handle both even and odd-length palindromes.\n - Insert special characters (commonly \'#\') between each pair of characters and at the beginning and end of the string.\n - For example, the string "aba" becomes $#a#b#a#.\n#### 2. **Initialize the Algorithm:**\n - Set up an array, `p`, to store information about palindromes.\n - The value `p[i]` in the array represents the radius of the palindrome centered at index `i`.\n - Initialize variables `center` and `right` to manage the exploration process.\n\n#### 3. **Explore Palindromes:**\n - Iterate through the transformed string efficiently using a center and right boundary.\n - Calculate the mirror of the current index with respect to the center to optimize computations.\n - Update the palindrome information in the `p` array based on the algorithm\'s findings.\n - Efficiently expand the palindrome around the current center, adjusting the center and right boundary as needed.\n\n#### 4. **Maintain Longest Palindrome:**\n - Throughout the algorithm\'s execution, keep track of the maximum palindrome found and its center index.\n - At the end of the process, retrieve the longest palindromic substring using the stored information.\n\n### \uD83D\uDCDDDry Run\nLet\'s apply Manacher\'s Algorithm to the input "babad":\n - Initialize the transformed string as "$#b#a#b#a#d#."\n - Iterate through the string efficiently using a center and right boundary.\n - Update the information in the `p` array based on the algorithm\'s findings.\n\n### \uD83D\uDD0DEdge Cases\nManacher\'s Algorithm gracefully handles various edge cases:\n - **Single-Character String:**\n - In this scenario, each character is considered a palindrome by itself.\n - **Empty String:**\n - The algorithm elegantly manages an empty string, resulting in an empty palindrome.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n - **Time Complexity:** O(n) - Manacher\'s Algorithm achieves linear time complexity, making it highly efficient.\n - **Space Complexity:** O(n) - The algorithm utilizes an array to store information about the palindromic nature of substrings.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes\n\n```cpp []\nclass Solution{\npublic:\nstring longestPalindrome(string s) {\n string newStr = "$#";\n for (char c : s) {\n newStr += c;\n newStr += \'#\';\n }\n\n int size = newStr.size();\n vector<int> p(size, 0);\n int center = 0, right = 0;\n\n for (int i = 1; i < size - 1; i++) {\n int mirror = 2 * center - i;\n\n if (i < right) {\n p[i] = min(right - i, p[mirror]);\n }\n\n // Attempt to expand palindrome centered at i\n while (newStr[i + (1 + p[i])] == newStr[i - (1 + p[i])]) {\n p[i]++;\n }\n\n // If palindrome centered at i expands past right,\n // adjust center and right boundary\n if (i + p[i] > right) {\n center = i;\n right = i + p[i];\n }\n }\n\n // Find the maximum element in P\n int maxLen = *max_element(p.begin(), p.end());\n int centerIndex = find(p.begin(), p.end(), maxLen) - p.begin();\n\n int start = (centerIndex - maxLen) / 2;\n return s.substr(start, maxLen);\n}\n};\n```\n\n```python []\nclass Solution:\n def preprocess(self, s):\n processed_string = "#"\n for char in s:\n processed_string += char + "#"\n return processed_string\n\n def longestPalindrome(self, s):\n processed_string = self.preprocess(s)\n size = len(processed_string)\n p = [0] * size\n center = 0\n right = 0\n\n for i in range(1, size - 1):\n mirror = 2 * center - i\n\n if i < right:\n p[i] = min(right - i, p[mirror])\n\n # Attempt to expand palindrome centered at i\n while (\n i + (1 + p[i]) < size\n and i - (1 + p[i]) >= 0\n and processed_string[i + (1 + p[i])] == processed_string[i - (1 + p[i])]\n ):\n p[i] += 1\n\n # If palindrome centered at i expands past right,\n # adjust center and right boundary\n if i + p[i] > right:\n center = i\n right = i + p[i]\n\n # Find the maximum element in P\n max_len = max(p)\n center_index = p.index(max_len)\n\n # Extract the palindrome substring from the processed string\n start = (center_index - max_len) // 2\n return s[start : start + max_len]\n\n\n```\n\n```java []\nclass Solution {\n private String preprocess(String s) {\n StringBuilder processedString = new StringBuilder("#");\n for (char c : s.toCharArray()) {\n processedString.append(c).append("#");\n }\n return processedString.toString();\n }\n\n // Manacher\'s algorithm function\n public String longestPalindrome(String s) {\n // Transform the input string\n String processedString = preprocess(s);\n\n int size = processedString.length();\n int[] p = new int[size];\n int center = 0, right = 0;\n\n for (int i = 1; i < size - 1; i++) {\n int mirror = 2 * center - i;\n\n if (i < right) {\n p[i] = Math.min(right - i, p[mirror]);\n }\n\n // Attempt to expand palindrome centered at i\n while (i + (1 + p[i]) < size && i - (1 + p[i]) >= 0 &&\n processedString.charAt(i + (1 + p[i])) == processedString.charAt(i - (1 + p[i]))) {\n p[i]++;\n }\n\n // If palindrome centered at i expands past right,\n // adjust center and right boundary\n if (i + p[i] > right) {\n center = i;\n right = i + p[i];\n }\n }\n\n // Find the maximum element in P\n int maxLen = 0, centerIndex = 0;\n for (int i = 1; i < size - 1; i++) {\n if (p[i] > maxLen) {\n maxLen = p[i];\n centerIndex = i;\n }\n }\n\n // Extract the palindrome substring from the processed string\n int start = (centerIndex - maxLen) / 2;\n return s.substring(start, start + maxLen);\n }\n \n}\n```\n\n```csharp []\npublic class Solution\n{\n private string Preprocess(string s)\n {\n var processedString = "#";\n foreach (var c in s)\n {\n processedString += c + "#";\n }\n return processedString;\n }\n\n public string LongestPalindrome(string s)\n {\n var processedString = Preprocess(s);\n var size = processedString.Length;\n var p = new int[size];\n var center = 0;\n var right = 0;\n\n for (var i = 1; i < size - 1; i++)\n {\n var mirror = 2 * center - i;\n\n if (i < right)\n {\n p[i] = Math.Min(right - i, p[mirror]);\n }\n\n // Attempt to expand palindrome centered at i\n while (i + (1 + p[i]) < size && i - (1 + p[i]) >= 0 &&\n processedString[i + (1 + p[i])] == processedString[i - (1 + p[i])])\n {\n p[i]++;\n }\n\n // If palindrome centered at i expands past right,\n // adjust center and right boundary\n if (i + p[i] > right)\n {\n center = i;\n right = i + p[i];\n }\n }\n\n // Find the maximum element in P\n var maxLen = p.Max();\n var centerIndex = Array.IndexOf(p, maxLen);\n\n // Extract the palindrome substring from the processed string\n var start = (centerIndex - maxLen) / 2;\n return s.Substring(start, maxLen);\n }\n}\n```\n\n```javascript []\n\n var longestPalindrome = function(s) {\n let newStr = "$#";\n for (const c of s) {\n newStr += c;\n newStr += \'#\';\n }\n\n const size = newStr.length;\n const p = Array(size).fill(0);\n let center = 0;\n let right = 0;\n\n for (let i = 1; i < size - 1; i++) {\n const mirror = 2 * center - i;\n\n if (i < right) {\n p[i] = Math.min(right - i, p[mirror]);\n }\n\n // Attempt to expand palindrome centered at i\n while (newStr[i + (1 + p[i])] === newStr[i - (1 + p[i])]) {\n p[i]++;\n }\n\n // If palindrome centered at i expands past right,\n // adjust center and right boundary\n if (i + p[i] > right) {\n center = i;\n right = i + p[i];\n }\n }\n\n // Find the maximum element in P\n const maxLen = Math.max(...p);\n const centerIndex = p.indexOf(maxLen);\n\n const start = Math.floor((centerIndex - maxLen) / 2);\n return s.substring(start, start + maxLen);\n };\n\n```\n\n```ruby []\n\ndef longest_palindrome(s)\n new_str = "$#"\n s.each_char do |c|\n new_str += c\n new_str += \'#\'\n end\n\n size = new_str.length\n p = Array.new(size, 0)\n center = 0\n right = 0\n\n (1...size - 1).each do |i|\n mirror = 2 * center - i\n\n if i < right\n p[i] = [right - i, p[mirror]].min\n end\n\n # Attempt to expand palindrome centered at i\n while new_str[i + (1 + p[i])] == new_str[i - (1 + p[i])]\n p[i] += 1\n end\n\n # If palindrome centered at i expands past right,\n # adjust center and right boundary\n if i + p[i] > right\n center = i\n right = i + p[i]\n end\n end\n\n # Find the maximum element in P\n max_len = p.max\n center_index = p.index(max_len)\n\n start = (center_index - max_len) / 2\n s[start, max_len]\n end\n\n```\n\n\n---\n\n## \uD83D\uDCCA Analysis\n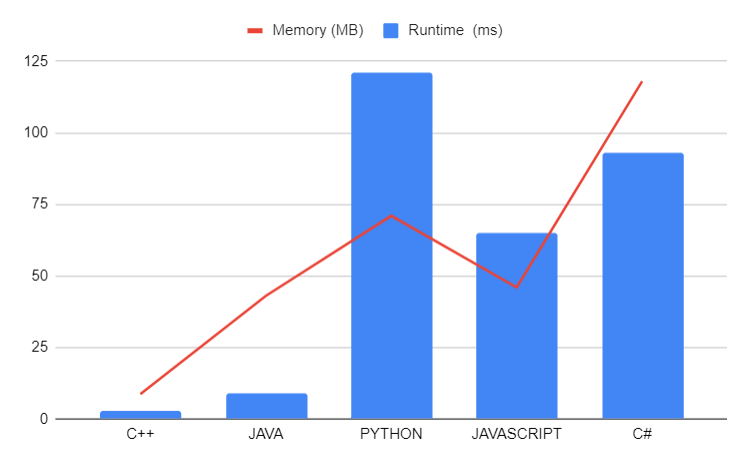\n\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|-------------|\n| C++ | 3 | 8.67 |\n| JAVA | 9 | 43 |\n| PYTHON | 121 | 71 |\n| JAVASCRIPT | 65 | 46 |\n| C# | 93 | 118 |\n\n\n---\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅Unlocking Palindromic Mastery: Leetcode Algorithmic Gems ✅3 Solution💡Beginner's Guide by Mr.Robot | longest-palindromic-substring | 1 | 1 | ### Welcome to the Blog you need to be a Pro-bro in this Problem\n---\n## \uD83D\uDCA1Approach 1: Middle Expansion - Explained in Depth\n\n### \u2728Explanation\nThe Middle Expansion approach is an intuitive method for finding the longest palindromic substring. The idea is to consider each character in the string as a potential center of a palindrome and expand outward to identify the longest palindrome. This method is effective for handling both odd and even-length palindromes.\n\n### \uD83D\uDCDDDetailed Explanation\n1. **Selecting the Center:**\n - Begin by iterating through each character in the string.\n - For each character, consider it as the potential center of a palindrome.\n\n2. **Expanding Outward:**\n - Expand outward from the center to identify palindromes.\n - For odd-length palindromes, expand in both directions.\n - For even-length palindromes, expand around the center two characters.\n\n3. **Updating Longest Palindrome:**\n - Keep track of the start and end indices of the longest palindrome found so far.\n\n### \uD83D\uDCDDDry Run\nLet\'s illustrate the Middle Expansion approach with the input "babad":\n- For \'b\', the expansion yields "b" (odd length).\n- For \'a\', the expansion yields "aba" (odd length).\n- For \'b\', the expansion yields "bab" (even length).\n- For \'a\', the expansion yields "a" (odd length).\n- For \'d\', the expansion yields "d" (odd length).\n\n### \uD83D\uDD0DEdge Cases\nThe Middle Expansion approach handles various edge cases:\n- **Single-Character String:**\n - In this case, each character is considered a palindrome by itself.\n- **Empty String:**\n - The algorithm gracefully handles an empty string, resulting in an empty palindrome.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- **Time Complexity:** O(n\xB2) - In the worst case, each character might be the center, and we expand on both sides.\n- **Space Complexity:** O(1) - We use constant space for variables.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCode \n\n```cpp []\nclass Solution{\nstring longestPalindrome(string s) {\n int start = 0;\n int resLen = 0;\n for(int i = 0; i < s.length(); i++) {\n // Odd length palindrome\n int left = i, right = i;\n while(left >= 0 && right < s.length() && s[left] == s[right]) {\n if(right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n \n // Even length palindrome\n left = i, right = i + 1;\n while(left >= 0 && right < s.length() && s[left] == s[right]) {\n if(right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n }\n return s.substr(start, resLen);\n}\n};\n```\n\n\n```java []\npublic class Solution {\n public String longestPalindrome(String s) {\n int start = 0;\n int resLen = 0;\n for (int i = 0; i < s.length(); i++) {\n // Odd length palindrome\n int left = i, right = i;\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n\n // Even length palindrome\n left = i;\n right = i + 1;\n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n }\n return s.substring(start, start + resLen);\n }\n}\n```\n\n```python []\nclass Solution: \n def longestPalindrome(self,s:str):\n start = 0\n res_len = 0\n for i in range(len(s)):\n # Odd length palindrome\n left, right = i, i\n while left >= 0 and right < len(s) and s[left] == s[right]:\n if right - left + 1 > res_len:\n start = left\n res_len = right - left + 1\n left -= 1\n right += 1\n\n # Even length palindrome\n left, right = i, i + 1\n while left >= 0 and right < len(s) and s[left] == s[right]:\n if right - left + 1 > res_len:\n start = left\n res_len = right - left + 1\n left -= 1\n right += 1\n return s[start:start + res_len]\n```\n\n```csharp []\npublic class Solution {\n public string LongestPalindrome(string s) {\n int start = 0;\n int resLen = 0;\n for (int i = 0; i < s.Length; i++) {\n // Odd length palindrome\n int left = i, right = i;\n while (left >= 0 && right < s.Length && s[left] == s[right]) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n\n // Even length palindrome\n left = i;\n right = i + 1;\n while (left >= 0 && right < s.Length && s[left] == s[right]) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n }\n return s.Substring(start, resLen);\n }\n}\n```\n\n```javascript []\nvar longestPalindrome = function(s) {\n let start = 0;\n let resLen = 0;\n for (let i = 0; i < s.length; i++) {\n // Odd length palindrome\n let left = i, right = i;\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n\n // Even length palindrome\n left = i;\n right = i + 1;\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n if (right - left + 1 > resLen) {\n start = left;\n resLen = right - left + 1;\n }\n left--;\n right++;\n }\n }\n return s.substring(start, start + resLen);\n};\n```\n---\n\n## \uD83D\uDCCA Analysis\n\n\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|--------------|\n| C++ | 10 | 7.26 |\n| JAVA | 20 | 40 |\n| PYTHON | 509 | 16.38 |\n| JAVASCRIPT | 68 | 42.72 |\n| C# | 82 | 37.48 |\n\n---\n\n---\n\n## \uD83D\uDCA1Approach 2: Dynamic Programming - Explained in Depth\n\n### \u2728Explanation\nDynamic Programming (DP) is a powerful technique that breaks down a problem into smaller subproblems and solves each subproblem only once, storing the results to avoid redundant computations. In the context of finding the longest palindromic substring, we can use dynamic programming to efficiently check and store information about palindromes.\n\n### \uD83D\uDCDDDetailed Explanation\n1. **Initialization:**\n - Initialize a 2D array, `dp`, where `dp[i][j]` will represent whether the substring from index `i` to `j` is a palindrome.\n - Set the diagonal elements and adjacent two-character substrings initially, as they are trivially palindromes.\n\n2. **Fill the DP Table:**\n - Iterate through the array, starting with larger substrings.\n - For each substring, check if the characters at both ends are equal and if the inner substring is a palindrome (lookup in the DP table).\n\n3. **Maintain Longest Palindrome:**\n - Update the start and end indices of the longest palindromic substring found so far.\n\n### \uD83D\uDCDDDry Run\nLet\'s apply dynamic programming to the input "babad":\n- The table is initialized based on single characters and two-character substrings.\n- For longer substrings, we check if the inner substring is a palindrome and the characters at the ends match.\n\n### \uD83D\uDD0DEdge Cases\nDynamic Programming handles various edge cases:\n- **Single-Character String:**\n - In this case, each character is considered a palindrome by itself.\n- **Empty String:**\n - The algorithm gracefully handles an empty string, resulting in an empty palindrome.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n- **Time Complexity:** O(n\xB2) - Filling the table takes quadratic time.\n- **Space Complexity:** O(n\xB2) - We use a 2D array to store information about the palindromic nature of substrings.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCode \n\n```cpp []\nclass Solution {\npublic:\n string longestPalindrome(string s) {\n int size = s.size();\n vector<vector<bool>> dp(size, vector<bool>(size));\n int start = 0, maxLen = 1;\n\n // Initialize for single characters\n for (int i = 0; i < size; i++) {\n dp[i][i] = true;\n }\n\n // Check for two-character substrings\n for (int i = 0; i < size - 1; i++) {\n if (s[i] == s[i + 1]) {\n dp[i][i + 1] = true;\n start = i;\n maxLen = 2;\n }\n }\n\n // Fill the rest of the table\n for (int col = 2; col < size; col++) {\n for (int row = 0; row < size - col; row++) {\n int cl = row + col;\n if (s[row] == s[cl] && dp[row + 1][cl - 1]) {\n dp[row][cl] = true;\n if (col + 1 > maxLen) {\n start = row;\n maxLen = col + 1;\n }\n }\n }\n }\n return s.substr(start, maxLen);\n}\n};\n```\n\n```java []\npublic class Solution {\n public String longestPalindrome(String s) {\n int size = s.length();\n boolean[][] dp = new boolean[size][size];\n int start = 0, maxLen = 1;\n\n // Initialize for single characters\n for (int i = 0; i < size; i++) {\n dp[i][i] = true;\n }\n\n // Check for two-character substrings\n for (int i = 0; i < size - 1; i++) {\n if (s.charAt(i) == s.charAt(i + 1)) {\n dp[i][i + 1] = true;\n start = i;\n maxLen = 2;\n }\n }\n\n // Fill the rest of the table\n for (int col = 2; col < size; col++) {\n for (int row = 0; row < size - col; row++) {\n int cl = row + col;\n if (s.charAt(row) == s.charAt(cl) && dp[row + 1][cl - 1]) {\n dp[row][cl] = true;\n if (col + 1 > maxLen) {\n start = row;\n maxLen = col + 1;\n }\n }\n }\n }\n return s.substring(start, start + maxLen);\n }\n}\n```\n\n```python []\nclass Solution:\n def longestPalindrome(self,s):\n size = len(s)\n dp = [[False] * size for _ in range(size)]\n start = 0\n max_len = 1\n\n # Initialize for single characters\n for i in range(size):\n dp[i][i] = True\n\n # Check for two-character substrings\n for i in range(size - 1):\n if s[i] == s[i + 1]:\n dp[i][i + 1] = True\n start = i\n max_len = 2\n\n # Fill the rest of the table\n for col in range(2, size):\n for row in range(size - col):\n cl = row + col\n if s[row] == s[cl] and dp[row + 1][cl - 1]:\n dp[row][cl] = True\n if col + 1 > max_len:\n start = row\n max_len = col + 1\n\n return s[start:start + max_len]\n```\n\n```csharp []\npublic class Solution {\n public string LongestPalindrome(string s) {\n int size = s.Length;\n bool[,] dp = new bool[size, size];\n int start = 0, maxLen = 1;\n\n // Initialize for single characters\n for (int i = 0; i < size; i++) {\n dp[i, i] = true;\n }\n\n // Check for two-character substrings\n for (int i = 0; i < size - 1; i++) {\n if (s[i] == s[i + 1]) {\n dp[i, i + 1] = true;\n start = i;\n maxLen = 2;\n }\n }\n\n // Fill the rest of the table\n for (int col = 2; col < size; col++) {\n for (int row = 0; row < size - col; row++) {\n int cl = row + col;\n if (s[row] == s[cl] && dp[row + 1, cl - 1]) {\n dp[row, cl] = true;\n if (col + 1 > maxLen) {\n start = row;\n maxLen = col + 1;\n }\n }\n }\n }\n return s.Substring(start, maxLen);\n }\n}\n```\n\n```javascript []\nvar longestPalindrome = function(s) {\n let size = s.length;\n let dp = Array.from(Array(size), () => Array(size).fill(false));\n let start = 0, maxLen = 1;\n\n // Initialize for single characters\n for (let i = 0; i < size; i++) {\n dp[i][i] = true;\n }\n\n // Check for two-character substrings\n for (let i = 0; i < size - 1; i++) {\n if (s[i] === s[i + 1]) {\n dp[i][i + 1] = true;\n start = i;\n maxLen = 2;\n }\n }\n\n // Fill the rest of the table\n for (let col = 2; col < size; col++) {\n for (let row = 0; row < size - col; row++) {\n let cl = row + col;\n if (s[row] === s[cl] && dp[row + 1][cl - 1]) {\n dp[row][cl] = true;\n if (col + 1 > maxLen) {\n start = row;\n maxLen = col + 1;\n }\n }\n }\n }\n return s.substring(start, start + maxLen);\n};\n```\n\n\n---\n\n## \uD83D\uDCCA Analysis\n\n\n\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|--------------|\n| C++ | 169 | 23 |\n| JAVA | 119 | 45.65 |\n| PYTHON | 2231 | 24.28 |\n| JAVASCRIPT | 364 | 87.11 |\n| C# | 110 | 42 |\n\n\n---\n\n\n---\n\n## \uD83D\uDCA1Approach 3: Manacher\'s Algorithm - A Detailed Exploration\n\n### \u2728Introduction\nManacher\'s Algorithm is a groundbreaking technique designed to find the longest palindromic substring in linear time, making it significantly more efficient than traditional methods. It takes advantage of the inherent symmetry in palindromes to optimize the search process.\n\n### \uD83D\uDCDDDetailed Explanation\n\n#### 1. **Transform the String:**\n - Manacher\'s Algorithm starts by transforming the input string to efficiently handle both even and odd-length palindromes.\n - Insert special characters (commonly \'#\') between each pair of characters and at the beginning and end of the string.\n - For example, the string "aba" becomes $#a#b#a#.\n#### 2. **Initialize the Algorithm:**\n - Set up an array, `p`, to store information about palindromes.\n - The value `p[i]` in the array represents the radius of the palindrome centered at index `i`.\n - Initialize variables `center` and `right` to manage the exploration process.\n\n#### 3. **Explore Palindromes:**\n - Iterate through the transformed string efficiently using a center and right boundary.\n - Calculate the mirror of the current index with respect to the center to optimize computations.\n - Update the palindrome information in the `p` array based on the algorithm\'s findings.\n - Efficiently expand the palindrome around the current center, adjusting the center and right boundary as needed.\n\n#### 4. **Maintain Longest Palindrome:**\n - Throughout the algorithm\'s execution, keep track of the maximum palindrome found and its center index.\n - At the end of the process, retrieve the longest palindromic substring using the stored information.\n\n### \uD83D\uDCDDDry Run\nLet\'s apply Manacher\'s Algorithm to the input "babad":\n - Initialize the transformed string as "$#b#a#b#a#d#."\n - Iterate through the string efficiently using a center and right boundary.\n - Update the information in the `p` array based on the algorithm\'s findings.\n\n### \uD83D\uDD0DEdge Cases\nManacher\'s Algorithm gracefully handles various edge cases:\n - **Single-Character String:**\n - In this scenario, each character is considered a palindrome by itself.\n - **Empty String:**\n - The algorithm elegantly manages an empty string, resulting in an empty palindrome.\n\n### \uD83D\uDD78\uFE0FComplexity Analysis\n - **Time Complexity:** O(n) - Manacher\'s Algorithm achieves linear time complexity, making it highly efficient.\n - **Space Complexity:** O(n) - The algorithm utilizes an array to store information about the palindromic nature of substrings.\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes\n\n```cpp []\nclass Solution{\npublic:\nstring longestPalindrome(string s) {\n string newStr = "$#";\n for (char c : s) {\n newStr += c;\n newStr += \'#\';\n }\n\n int size = newStr.size();\n vector<int> p(size, 0);\n int center = 0, right = 0;\n\n for (int i = 1; i < size - 1; i++) {\n int mirror = 2 * center - i;\n\n if (i < right) {\n p[i] = min(right - i, p[mirror]);\n }\n\n // Attempt to expand palindrome centered at i\n while (newStr[i + (1 + p[i])] == newStr[i - (1 + p[i])]) {\n p[i]++;\n }\n\n // If palindrome centered at i expands past right,\n // adjust center and right boundary\n if (i + p[i] > right) {\n center = i;\n right = i + p[i];\n }\n }\n\n // Find the maximum element in P\n int maxLen = *max_element(p.begin(), p.end());\n int centerIndex = find(p.begin(), p.end(), maxLen) - p.begin();\n\n int start = (centerIndex - maxLen) / 2;\n return s.substr(start, maxLen);\n}\n};\n```\n\n```python []\nclass Solution:\n def preprocess(self, s):\n processed_string = "#"\n for char in s:\n processed_string += char + "#"\n return processed_string\n\n def longestPalindrome(self, s):\n processed_string = self.preprocess(s)\n size = len(processed_string)\n p = [0] * size\n center = 0\n right = 0\n\n for i in range(1, size - 1):\n mirror = 2 * center - i\n\n if i < right:\n p[i] = min(right - i, p[mirror])\n\n # Attempt to expand palindrome centered at i\n while (\n i + (1 + p[i]) < size\n and i - (1 + p[i]) >= 0\n and processed_string[i + (1 + p[i])] == processed_string[i - (1 + p[i])]\n ):\n p[i] += 1\n\n # If palindrome centered at i expands past right,\n # adjust center and right boundary\n if i + p[i] > right:\n center = i\n right = i + p[i]\n\n # Find the maximum element in P\n max_len = max(p)\n center_index = p.index(max_len)\n\n # Extract the palindrome substring from the processed string\n start = (center_index - max_len) // 2\n return s[start : start + max_len]\n\n\n```\n\n```java []\nclass Solution {\n private String preprocess(String s) {\n StringBuilder processedString = new StringBuilder("#");\n for (char c : s.toCharArray()) {\n processedString.append(c).append("#");\n }\n return processedString.toString();\n }\n\n // Manacher\'s algorithm function\n public String longestPalindrome(String s) {\n // Transform the input string\n String processedString = preprocess(s);\n\n int size = processedString.length();\n int[] p = new int[size];\n int center = 0, right = 0;\n\n for (int i = 1; i < size - 1; i++) {\n int mirror = 2 * center - i;\n\n if (i < right) {\n p[i] = Math.min(right - i, p[mirror]);\n }\n\n // Attempt to expand palindrome centered at i\n while (i + (1 + p[i]) < size && i - (1 + p[i]) >= 0 &&\n processedString.charAt(i + (1 + p[i])) == processedString.charAt(i - (1 + p[i]))) {\n p[i]++;\n }\n\n // If palindrome centered at i expands past right,\n // adjust center and right boundary\n if (i + p[i] > right) {\n center = i;\n right = i + p[i];\n }\n }\n\n // Find the maximum element in P\n int maxLen = 0, centerIndex = 0;\n for (int i = 1; i < size - 1; i++) {\n if (p[i] > maxLen) {\n maxLen = p[i];\n centerIndex = i;\n }\n }\n\n // Extract the palindrome substring from the processed string\n int start = (centerIndex - maxLen) / 2;\n return s.substring(start, start + maxLen);\n }\n \n}\n```\n\n```csharp []\npublic class Solution\n{\n private string Preprocess(string s)\n {\n var processedString = "#";\n foreach (var c in s)\n {\n processedString += c + "#";\n }\n return processedString;\n }\n\n public string LongestPalindrome(string s)\n {\n var processedString = Preprocess(s);\n var size = processedString.Length;\n var p = new int[size];\n var center = 0;\n var right = 0;\n\n for (var i = 1; i < size - 1; i++)\n {\n var mirror = 2 * center - i;\n\n if (i < right)\n {\n p[i] = Math.Min(right - i, p[mirror]);\n }\n\n // Attempt to expand palindrome centered at i\n while (i + (1 + p[i]) < size && i - (1 + p[i]) >= 0 &&\n processedString[i + (1 + p[i])] == processedString[i - (1 + p[i])])\n {\n p[i]++;\n }\n\n // If palindrome centered at i expands past right,\n // adjust center and right boundary\n if (i + p[i] > right)\n {\n center = i;\n right = i + p[i];\n }\n }\n\n // Find the maximum element in P\n var maxLen = p.Max();\n var centerIndex = Array.IndexOf(p, maxLen);\n\n // Extract the palindrome substring from the processed string\n var start = (centerIndex - maxLen) / 2;\n return s.Substring(start, maxLen);\n }\n}\n```\n\n```javascript []\n\n var longestPalindrome = function(s) {\n let newStr = "$#";\n for (const c of s) {\n newStr += c;\n newStr += \'#\';\n }\n\n const size = newStr.length;\n const p = Array(size).fill(0);\n let center = 0;\n let right = 0;\n\n for (let i = 1; i < size - 1; i++) {\n const mirror = 2 * center - i;\n\n if (i < right) {\n p[i] = Math.min(right - i, p[mirror]);\n }\n\n // Attempt to expand palindrome centered at i\n while (newStr[i + (1 + p[i])] === newStr[i - (1 + p[i])]) {\n p[i]++;\n }\n\n // If palindrome centered at i expands past right,\n // adjust center and right boundary\n if (i + p[i] > right) {\n center = i;\n right = i + p[i];\n }\n }\n\n // Find the maximum element in P\n const maxLen = Math.max(...p);\n const centerIndex = p.indexOf(maxLen);\n\n const start = Math.floor((centerIndex - maxLen) / 2);\n return s.substring(start, start + maxLen);\n };\n\n```\n\n```ruby []\n\ndef longest_palindrome(s)\n new_str = "$#"\n s.each_char do |c|\n new_str += c\n new_str += \'#\'\n end\n\n size = new_str.length\n p = Array.new(size, 0)\n center = 0\n right = 0\n\n (1...size - 1).each do |i|\n mirror = 2 * center - i\n\n if i < right\n p[i] = [right - i, p[mirror]].min\n end\n\n # Attempt to expand palindrome centered at i\n while new_str[i + (1 + p[i])] == new_str[i - (1 + p[i])]\n p[i] += 1\n end\n\n # If palindrome centered at i expands past right,\n # adjust center and right boundary\n if i + p[i] > right\n center = i\n right = i + p[i]\n end\n end\n\n # Find the maximum element in P\n max_len = p.max\n center_index = p.index(max_len)\n\n start = (center_index - max_len) / 2\n s[start, max_len]\n end\n\n```\n\n\n---\n\n## \uD83D\uDCCA Analysis\n\n\n| Language | Runtime (ms) | Memory (MB) |\n|------------|--------------|-------------|\n| C++ | 3 | 8.67 |\n| JAVA | 9 | 43 |\n| PYTHON | 121 | 71 |\n| JAVASCRIPT | 65 | 46 |\n| C# | 93 | 118 |\n\n\n---\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF*\n | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
python3 | longest-palindromic-substring | 0 | 1 | \n# Complexity\n- Time complexity:\n- O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n n=len(s)\n m="" \n def helper1(i):\n nonlocal m\n l=i\n r=i\n while(0<=l and r<n and s[l]==s[r]):\n if(len(m)<r-l+1):\n m=s[l:r+1]\n l=l-1\n r=r+1\n return\n def helper2(i):\n nonlocal m\n l=i\n r=i+1\n while(0<=l and r<n and s[l]==s[r]):\n if(len(m)<r-l+1):\n m=s[l:r+1]\n l=l-1\n r=r+1\n return\n\n for i in range(0,len(s)):\n helper1(i)\n helper2(i)\n return m\n``` | 2 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
python3 | longest-palindromic-substring | 0 | 1 | \n# Complexity\n- Time complexity:\n- O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n n=len(s)\n m="" \n def helper1(i):\n nonlocal m\n l=i\n r=i\n while(0<=l and r<n and s[l]==s[r]):\n if(len(m)<r-l+1):\n m=s[l:r+1]\n l=l-1\n r=r+1\n return\n def helper2(i):\n nonlocal m\n l=i\n r=i+1\n while(0<=l and r<n and s[l]==s[r]):\n if(len(m)<r-l+1):\n m=s[l:r+1]\n l=l-1\n r=r+1\n return\n\n for i in range(0,len(s)):\n helper1(i)\n helper2(i)\n return m\n``` | 2 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅☑[C++/Java/Python/JavaScript] || 4 Approaches || EXPLAINED🔥 | longest-palindromic-substring | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Brute Approach)***\n1. The `longestPalindrome` function is the main function for finding the longest palindromic substring.\n\n1. It first preprocesses the input string `s` to create a new string `sPrime` that contains \'#\' characters between each character of the original string. This is done to handle both even and odd length palindromes more uniformly.\n\n1. It calculates the length of `sPrime` and initializes a vector `palindromeRadii` with the same length. The `palindromeRadii` vector will store the lengths of the palindromes centered at each position in `sPrime`.\n\n1. The code initializes two variables, `center` and `radius`, to keep track of the center and right boundary of the rightmost known palindrome.\n\n1. It then enters a loop that iterates over each character in `sPrime` (and its corresponding position in the original s).\n\n1. For each character, it calculates a mirror index `mirror` with respect to the current `center`. If the current character is within the current palindrome (i.e., `i < radius`), it updates the `palindromeRadii` with the minimum of the distance from the right boundary and the corresponding mirror value.\n\n1. The code then attempts to expand the palindrome centered at the current character. It uses a while loop to compare characters symmetrically around the current position (with `i` as the center), extending the palindrome if the characters match. It increments `palindromeRadii[i]` accordingly.\n\n1. If the extended palindrome goes beyond the right boundary, it updates the `center` and `radius` to the current character.\n\n1. After processing all characters, the code finds the maximum value in the `palindromeRadii` vector, which represents the length of the longest palindrome. It also determines the index of the center of this longest palindrome.\n\n1. With the center index and the palindrome length, it calculates the start index of the palindrome within the original string `s`.\n\n1. Finally, it returns the longest palindromic substring by using the `substr` function to extract the substring from the original input string `s` using the calculated start index and palindrome length.\n\n# Complexity\n- *Time complexity:*\n $$O(n^3)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\n\nclass Solution {\npublic:\n bool check (int i,int j , string s){\n while(i<=j){\n if(s[i] != s[j]){\n return false;\n }else{\n i++;\n j--;\n }\n }\n return true;\n }\n string longestPalindrome(string s) {\n int maxlen=0;\n int index =0;\n for(int i =0;i<s.size();i++){\n for(int j =i;j<s.size();j++){\n if(s[i]==s[j]){\n bool ans = check(i,j,s);\n if(ans){\n if(j-i+1 > maxlen){\n maxlen = j-i+1;\n index =i;\n }\n }\n }\n }\n }\n return s.substr(index,maxlen);\n }\n};\n\n```\n```C []\n\n\n\nbool check(int i, int j, const char *s) {\n int left = i;\n int right = j - 1;\n\n while (left < right) {\n if (s[left] != s[right]) {\n return false;\n }\n\n left++;\n right--;\n }\n\n return true;\n}\n\nchar *longestPalindrome(char *s) {\n int len = strlen(s);\n\n for (int length = len; length > 0; length--) {\n for (int start = 0; start <= len - length; start++) {\n if (check(start, start + length, s)) {\n char *result = (char *)malloc(length + 1);\n strncpy(result, s + start, length);\n result[length] = \'\\0\';\n return result;\n }\n }\n }\n\n char *result = (char *)malloc(1);\n result[0] = \'\\0\';\n return result;\n}\n\n\n\n```\n```Java []\n\nclass Solution {\n public String longestPalindrome(String s) {\n for (int length = s.length(); length > 0; length--) {\n for (int start = 0; start <= s.length() - length; start++) {\n if (check(start, start + length, s)) {\n return s.substring(start, start + length);\n }\n }\n }\n \n return "";\n }\n \n private boolean check(int i, int j, String s) {\n int left = i;\n int right = j - 1;\n \n while (left < right) {\n if (s.charAt(left) != s.charAt(right)) {\n return false;\n }\n \n left++;\n right--;\n }\n \n return true;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n def check(i, j):\n left = i\n right = j - 1\n \n while left < right:\n if s[left] != s[right]:\n return False\n \n left += 1\n right -= 1\n \n return True\n \n for length in range(len(s), 0, -1):\n for start in range(len(s) - length + 1):\n if check(start, start + length):\n return s[start:start + length]\n\n return ""\n\n\n```\n```javascript []\nvar longestPalindrome = function (s) {\n function check(i, j, s) {\n let left = i;\n let right = j - 1;\n \n while (left < right) {\n if (s[left] !== s[right]) {\n return false;\n }\n \n left++;\n right--;\n }\n \n return true;\n }\n\n for (let length = s.length; length > 0; length--) {\n for (let start = 0; start <= s.length - length; start++) {\n if (check(start, start + length, s)) {\n return s.substring(start, start + length);\n }\n }\n }\n\n return "";\n};\n\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log(result); // Output: "bab" or "aba"\n\n```\n\n\n---\n\n#### ***Approach 2(DP)***\n1. The `longestPalindrome` function is the main function for finding the longest palindromic substring.\n\n1. It initializes a vector `ans` to store the indices of the start and end of the longest palindrome found. Initially, it\'s set to {0, 0}, indicating no palindrome.\n\n1. The code iterates through each character in the input string `s` using a for loop with index `i`.\n\n1. Inside the loop, it first finds the length of the longest odd-length palindrome centered at the current character `i`. It does this by calling the `expand` function with the same `i` for both `left` and `right` indices. If this odd-length palindrome is longer than the previously found palindrome, it updates the `ans` vector with the new indices.\n\n1. Next, it finds the length of the longest even-length palindrome centered at the current character `i` and the next character `i+1`. It does this by calling the `expand` function with `i` and `i+1` as `left` and `right`. If this even-length palindrome is longer than the previously found palindrome, it updates the `ans` vector with the new indices.\n\n1. The code continues iterating through the string, updating `ans` as it finds longer palindromes.\n\n1. After the loop, the `i` and `j` values in the `ans` vector represent the start and end indices of the longest palindrome.\n\n1. Finally, it returns the longest palindrome by using the `substr` function to extract the substring from the input string s using the start and end indices.\n\n1. The `expand` function is a helper function that takes indices `i` and `j` and the input string `s` and returns the length of the palindrome that can be expanded from these indices. It expands the palindrome by moving the `left` and `right` indices towards the center until they no longer match or reach the string boundaries. The length of the palindrome is determined by the difference between `right` and `left`, minus 1, since it includes both `i` and `j`.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(n^2)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n string longestPalindrome(string s) {\n vector<int> ans = {0, 0};\n\n for (int i = 0; i < s.length(); i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int i = ans[0];\n int j = ans[1];\n return s.substr(i, j - i + 1);\n }\n\nprivate:\n int expand(int i, int j, string s) {\n int left = i;\n int right = j;\n\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n }\n};\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n#include <string.h>\n\nchar *longestPalindrome(char *s) {\n int n = strlen(s);\n int ans[2] = {0, 0};\n\n for (int i = 0; i < n; i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int start = ans[0];\n int end = ans[1];\n char *result = (char *)malloc((end - start + 2) * sizeof(char));\n strncpy(result, s + start, end - start + 1);\n result[end - start + 1] = \'\\0\';\n return result;\n}\n\nint expand(int i, int j, char *s) {\n int left = i;\n int right = j;\n\n while (left >= 0 && right < strlen(s) && s[left] == s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n}\n\nint main() {\n char s[] = "babad";\n char *result = longestPalindrome(s);\n printf("%s\\n", result); // Output: "bab" or "aba"\n free(result);\n return 0;\n}\n\n\n\n```\n```Java []\n\nclass Solution {\n public String longestPalindrome(String s) {\n int n = s.length();\n boolean[][] dp = new boolean[n][n];\n int[] ans = new int[]{0, 0};\n \n for (int i = 0; i < n; i++) {\n dp[i][i] = true;\n }\n \n for (int i = 0; i < n - 1; i++) {\n if (s.charAt(i) == s.charAt(i + 1)) {\n dp[i][i + 1] = true;\n ans[0] = i;\n ans[1] = i + 1;\n }\n }\n \n for (int diff = 2; diff < n; diff++) {\n for (int i = 0; i < n - diff; i++) {\n int j = i + diff;\n if (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {\n dp[i][j] = true;\n ans[0] = i;\n ans[1] = j;\n }\n }\n }\n \n int i = ans[0];\n int j = ans[1];\n return s.substring(i, j + 1);\n }\n}\n\n```\n```python3 []\n\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n n = len(s)\n dp = [[False] * n for _ in range(n)]\n ans = [0, 0]\n \n for i in range(n):\n dp[i][i] = True\n \n for i in range(n - 1):\n if s[i] == s[i + 1]:\n dp[i][i + 1] = True\n ans = [i, i + 1]\n\n for diff in range(2, n):\n for i in range(n - diff):\n j = i + diff\n if s[i] == s[j] and dp[i + 1][j - 1]:\n dp[i][j] = True\n ans = [i, j]\n\n i, j = ans\n return s[i:j + 1]\n\n```\n```javascript []\nvar longestPalindrome = function (s) {\n let ans = [0, 0];\n\n for (let i = 0; i < s.length; i++) {\n let oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n let dist = Math.floor(oddLength / 2);\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n let evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n let dist = Math.floor(evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n let start = ans[0];\n let end = ans[1];\n return s.slice(start, end + 1);\n};\n\nfunction expand(i, j, s) {\n let left = i;\n let right = j;\n\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n}\n\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log(result); // Output: "bab" or "aba"\n\n```\n\n\n---\n#### ***Approach 3(Expand From Center)***\n1. The `longestPalindrome` function is the main function for finding the longest palindromic substring.\n\n1. It initializes a vector `ans` to store the indices of the start and end of the longest palindrome found. Initially, it\'s set to {0, 0}, indicating no palindrome.\n\n1. The code iterates through each character in the input string `s` using a for loop with index `i`.\n\n1. Inside the loop, it first finds the length of the longest odd-length palindrome centered at the current character `i`. It does this by calling the `expand` function with the same `i` for both `left` and `right` indices. If this odd-length palindrome is longer than the previously found palindrome, it updates the `ans` vector with the new indices.\n\n1. Next, it finds the length of the longest even-length palindrome centered at the current character `i` and the next character `i+1`. It does this by calling the `expand` function with i and `i+1` as `left` and `right`. If this even-length palindrome is longer than the previously found palindrome, it updates the `ans` vector with the new indices.\n\n1. The code continues iterating through the string, updating `ans` as it finds longer palindromes.\n\n1. After the loop, the `start` and `end` values in the `ans` vector represent the start and end indices of the longest palindrome.\n\n1. Finally, it returns the longest palindrome by using the `substr` function to extract the substring from the input string `s` using the start and end indices. The length of the substring is calculated by subtracting the start index from the end index and adding 1 to include the character at the end.\n\n1. The `expand` function is a helper function that takes indices `i` and `j`, as well as the input string `s`, and returns the length of the palindrome that can be expanded from these indices. It expands the palindrome by moving the `left` and `right` indices towards the center until they no longer match or reach the string boundaries. The length of the palindrome is determined by the difference between `right` and `left`, minus 1, since it includes both `i` and `j`.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\n\n\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n std::vector<int> ans = {0, 0};\n\n for (int i = 0; i < s.length(); i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int start = ans[0];\n int end = ans[1];\n return s.substr(start, end - start + 1);\n }\n\nprivate:\n int expand(int i, int j, const std::string &s) {\n int left = i;\n int right = j;\n\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n }\n};\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <string.h>\n#include <stdlib.h>\n\nint expand(int i, int j, const char *s) {\n int left = i;\n int right = j;\n\n while (left >= 0 && right < strlen(s) && s[left] == s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n}\n\nchar *longestPalindrome(char *s) {\n int ans[2] = {0, 0};\n\n for (int i = 0; i < strlen(s); i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int start = ans[0];\n int end = ans[1];\n int len = end - start + 1;\n char *result = (char *)malloc(len + 1);\n strncpy(result, s + start, len);\n result[len] = \'\\0\';\n return result;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public String longestPalindrome(String s) {\n int[] ans = new int[]{0, 0};\n \n for (int i = 0; i < s.length(); i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n \n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int i = ans[0];\n int j = ans[1];\n return s.substring(i, j + 1);\n }\n \n private int expand(int i, int j, String s) {\n int left = i;\n int right = j;\n \n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n left--;\n right++;\n }\n\n return right - left - 1;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n def expand(i, j):\n left = i\n right = j\n \n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n \n return right - left - 1\n \n ans = [0, 0]\n\n for i in range(len(s)):\n odd_length = expand(i, i)\n if odd_length > ans[1] - ans[0] + 1:\n dist = odd_length // 2\n ans = [i - dist, i + dist]\n\n even_length = expand(i, i + 1)\n if even_length > ans[1] - ans[0] + 1:\n dist = (even_length // 2) - 1\n ans = [i - dist, i + 1 + dist]\n \n i, j = ans\n return s[i:j + 1]\n\n\n```\n```javascript []\nvar longestPalindrome = function (s) {\n let ans = [0, 0];\n\n for (let i = 0; i < s.length; i++) {\n let oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n let dist = Math.floor(oddLength / 2);\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n let evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n let dist = Math.floor(evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n let start = ans[0];\n let end = ans[1];\n return s.substring(start, end + 1);\n};\n\nfunction expand(i, j, s) {\n let left = i;\n let right = j;\n\n while (left >= 0 && right < s.length && s.charAt(left) === s.charAt(right)) {\n left--;\n right++;\n }\n\n return right - left - 1;\n}\n\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log(result); // Output: "bab" or "aba"\n\n```\n\n\n---\n#### ***Approach 4(Manacher\'s Algorithm)***\n1. The `longestPalindrome` function is the main function for finding the longest palindromic substring.\n\n1. It first preprocesses the input string `s` to create a new string `sPrime` that contains `#` characters between each character of the original string. This is done to handle both even and odd length palindromes more uniformly.\n\n1. It calculates the length of `sPrime` and initializes a vector `palindromeRadii` with the same length. The `palindromeRadii` vector will store the lengths of the palindromes centered at each position in `sPrime`.\n\n1. The code initializes two variables, `center` and `radius`, to keep track of the center and right boundary of the rightmost known palindrome.\n\n1. It then enters a loop that iterates over each character in `sPrime` (and its corresponding position in the original `s`).\n\n1. For each character, it calculates a mirror index `mirror` with respect to the current `center`. If the current character is within the current palindrome (i.e., `i < radius`), it updates the `palindromeRadii` with the minimum of the distance from the right boundary and the corresponding mirror value.\n\n1. The code then attempts to expand the palindrome centered at the current character. It uses a while loop to compare characters symmetrically around the current position (with `i` as the center), extending the palindrome if the characters match. It increments `palindromeRadii[i]` accordingly.\n\n1. If the extended palindrome goes beyond the right boundary, it updates the `center` and `radius` to the current character.\n\n1. After processing all characters, the code finds the maximum value in the `palindromeRadii` vector, which represents the length of the longest palindrome. It also determines the index of the center of this longest palindrome.\n\n1. With the center index and the palindrome length, it calculates the start index of the palindrome within the original string `s`.\n\n1. Finally, it returns the longest palindromic substring by using the `substr` function to extract the substring from the original input string `s` using the calculated start index and palindrome length.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\n\n\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n std::string sPrime = "#";\n for (char c : s) {\n sPrime += \'#\';\n sPrime.push_back(c);\n }\n sPrime += \'#\';\n\n int n = sPrime.length();\n std::vector<int> palindromeRadii(n, 0);\n int center = 0;\n int radius = 0;\n\n for (int i = 0; i < n; i++) {\n int mirror = 2 * center - i;\n\n if (i < radius) {\n palindromeRadii[i] = std::min(radius - i, palindromeRadii[mirror]);\n }\n\n while (i + 1 + palindromeRadii[i] < n &&\n i - 1 - palindromeRadii[i] >= 0 &&\n sPrime[i + 1 + palindromeRadii[i]] == sPrime[i - 1 - palindromeRadii[i]]) {\n palindromeRadii[i]++;\n }\n\n if (i + palindromeRadii[i] > radius) {\n center = i;\n radius = i + palindromeRadii[i];\n }\n }\n\n int maxLength = *std::max_element(palindromeRadii.begin(), palindromeRadii.end());\n int centerIndex = std::distance(palindromeRadii.begin(), std::max_element(palindromeRadii.begin(), palindromeRadii.end()));\n int startIndex = (centerIndex - maxLength) / 2;\n std::string longestPalindrome = s.substr(startIndex, maxLength);\n\n return longestPalindrome;\n }\n};\n\n```\n```C []\n\nchar* longestPalindrome(char* s) {\n int len = strlen(s);\n char sPrime[2 * len + 1];\n int k = 0;\n\n for (int i = 0; i < len; i++) {\n sPrime[k++] = \'#\';\n sPrime[k++] = s[i];\n }\n sPrime[k++] = \'#\';\n sPrime[k] = \'\\0\';\n\n int n = 2 * len + 1;\n int* palindromeRadii = (int*)malloc(n * sizeof(int));\n\n int center = 0;\n int radius = 0;\n\n for (int i = 0; i < n; i++) {\n int mirror = 2 * center - i;\n\n if (i < radius) {\n palindromeRadii[i] = (radius - i) < palindromeRadii[mirror] ? (radius - i) : palindromeRadii[mirror];\n }\n\n while (i + 1 + palindromeRadii[i] < n && i - 1 - palindromeRadii[i] >= 0 && sPrime[i + 1 + palindromeRadii[i]] == sPrime[i - 1 - palindromeRadii[i]]) {\n palindromeRadii[i]++;\n }\n\n if (i + palindromeRadii[i] > radius) {\n center = i;\n radius = i + palindromeRadii[i];\n }\n }\n\n int maxLength = 0;\n int centerIndex = 0;\n for (int i = 0; i < n; i++) {\n if (palindromeRadii[i] > maxLength) {\n maxLength = palindromeRadii[i];\n centerIndex = i;\n }\n }\n\n int startIndex = (centerIndex - maxLength) / 2;\n char* longestPalindrome = (char*)malloc((maxLength + 1) * sizeof(char));\n strncpy(longestPalindrome, s + startIndex, maxLength);\n longestPalindrome[maxLength] = \'\\0\';\n\n free(palindromeRadii);\n return longestPalindrome;\n}\n\n\n```\n```Java []\n\nclass Solution {\n public String longestPalindrome(String s) {\n StringBuilder sPrime = new StringBuilder("#");\n for (char c: s.toCharArray()) {\n sPrime.append(c).append("#");\n }\n \n int n = sPrime.length();\n int[] palindromeRadii = new int[n];\n int center = 0;\n int radius = 0;\n \n for (int i = 0; i < n; i++) {\n int mirror = 2 * center - i;\n \n if (i < radius) {\n palindromeRadii[i] = Math.min(radius - i, palindromeRadii[mirror]);\n }\n \n while (i + 1 + palindromeRadii[i] < n &&\n i - 1 - palindromeRadii[i] >= 0 &&\n sPrime.charAt(i + 1 + palindromeRadii[i]) == sPrime.charAt(i - 1 - palindromeRadii[i])) {\n palindromeRadii[i]++;\n }\n \n if (i + palindromeRadii[i] > radius) {\n center = i;\n radius = i + palindromeRadii[i];\n }\n }\n \n int maxLength = 0;\n int centerIndex = 0;\n for (int i = 0; i < n; i++) {\n if (palindromeRadii[i] > maxLength) {\n maxLength = palindromeRadii[i];\n centerIndex = i;\n }\n }\n \n int startIndex = (centerIndex - maxLength) / 2;\n String longestPalindrome = s.substring(startIndex, startIndex + maxLength);\n \n return longestPalindrome;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n s_prime = \'#\' + \'#\'.join(s) + \'#\'\n n = len(s_prime)\n palindrome_radii = [0] * n\n center = radius = 0\n \n for i in range(n):\n mirror = 2 * center - i\n\n if i < radius:\n palindrome_radii[i] = min(radius - i, palindrome_radii[mirror])\n\n while (i + 1 + palindrome_radii[i] < n and \n i - 1 - palindrome_radii[i] >= 0 and\n s_prime[i + 1 + palindrome_radii[i]] == s_prime[i - 1 - palindrome_radii[i]]):\n palindrome_radii[i] += 1\n\n if i + palindrome_radii[i] > radius:\n center = i\n radius = i + palindrome_radii[i]\n\n max_length = max(palindrome_radii)\n center_index = palindrome_radii.index(max_length)\n start_index = (center_index - max_length) // 2\n longest_palindrome = s[start_index: start_index + max_length]\n\n return longest_palindrome\n\n\n```\n```javascript []\nvar longestPalindrome = function (s) {\n let sPrime = \'#\';\n\n for (let i = 0; i < s.length; i++) {\n sPrime += \'#\';\n sPrime += s[i];\n }\n\n sPrime += \'#\';\n\n const n = sPrime.length;\n const palindromeRadii = new Array(n).fill(0);\n let center = 0;\n let radius = 0;\n\n for (let i = 0; i < n; i++) {\n const mirror = 2 * center - i;\n\n if (i < radius) {\n palindromeRadii[i] = Math.min(radius - i, palindromeRadii[mirror]);\n }\n\n while (i + 1 + palindromeRadii[i] < n &&\n i - 1 - palindromeRadii[i] >= 0 &&\n sPrime[i + 1 + palindromeRadii[i]] === sPrime[i - 1 - palindromeRadii[i]) {\n palindromeRadii[i]++;\n }\n\n if (i + palindromeRadii[i] > radius) {\n center = i;\n radius = i + palindromeRadii[i];\n }\n }\n\n let maxLength = 0;\n let centerIndex = 0;\n\n for (let i = 0; i < n; i++) {\n if (palindromeRadii[i] > maxLength) {\n maxLength = palindromeRadii[i];\n centerIndex = i;\n }\n }\n\n const startIndex = Math.floor((centerIndex - maxLength) / 2);\n return s.substring(startIndex, startIndex + maxLength);\n};\n\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log(result); // Output: "bab" or "aba"\n\n```\n\n\n---\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅☑[C++/Java/Python/JavaScript] || 4 Approaches || EXPLAINED🔥 | longest-palindromic-substring | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Brute Approach)***\n1. The `longestPalindrome` function is the main function for finding the longest palindromic substring.\n\n1. It first preprocesses the input string `s` to create a new string `sPrime` that contains \'#\' characters between each character of the original string. This is done to handle both even and odd length palindromes more uniformly.\n\n1. It calculates the length of `sPrime` and initializes a vector `palindromeRadii` with the same length. The `palindromeRadii` vector will store the lengths of the palindromes centered at each position in `sPrime`.\n\n1. The code initializes two variables, `center` and `radius`, to keep track of the center and right boundary of the rightmost known palindrome.\n\n1. It then enters a loop that iterates over each character in `sPrime` (and its corresponding position in the original s).\n\n1. For each character, it calculates a mirror index `mirror` with respect to the current `center`. If the current character is within the current palindrome (i.e., `i < radius`), it updates the `palindromeRadii` with the minimum of the distance from the right boundary and the corresponding mirror value.\n\n1. The code then attempts to expand the palindrome centered at the current character. It uses a while loop to compare characters symmetrically around the current position (with `i` as the center), extending the palindrome if the characters match. It increments `palindromeRadii[i]` accordingly.\n\n1. If the extended palindrome goes beyond the right boundary, it updates the `center` and `radius` to the current character.\n\n1. After processing all characters, the code finds the maximum value in the `palindromeRadii` vector, which represents the length of the longest palindrome. It also determines the index of the center of this longest palindrome.\n\n1. With the center index and the palindrome length, it calculates the start index of the palindrome within the original string `s`.\n\n1. Finally, it returns the longest palindromic substring by using the `substr` function to extract the substring from the original input string `s` using the calculated start index and palindrome length.\n\n# Complexity\n- *Time complexity:*\n $$O(n^3)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\n\nclass Solution {\npublic:\n bool check (int i,int j , string s){\n while(i<=j){\n if(s[i] != s[j]){\n return false;\n }else{\n i++;\n j--;\n }\n }\n return true;\n }\n string longestPalindrome(string s) {\n int maxlen=0;\n int index =0;\n for(int i =0;i<s.size();i++){\n for(int j =i;j<s.size();j++){\n if(s[i]==s[j]){\n bool ans = check(i,j,s);\n if(ans){\n if(j-i+1 > maxlen){\n maxlen = j-i+1;\n index =i;\n }\n }\n }\n }\n }\n return s.substr(index,maxlen);\n }\n};\n\n```\n```C []\n\n\n\nbool check(int i, int j, const char *s) {\n int left = i;\n int right = j - 1;\n\n while (left < right) {\n if (s[left] != s[right]) {\n return false;\n }\n\n left++;\n right--;\n }\n\n return true;\n}\n\nchar *longestPalindrome(char *s) {\n int len = strlen(s);\n\n for (int length = len; length > 0; length--) {\n for (int start = 0; start <= len - length; start++) {\n if (check(start, start + length, s)) {\n char *result = (char *)malloc(length + 1);\n strncpy(result, s + start, length);\n result[length] = \'\\0\';\n return result;\n }\n }\n }\n\n char *result = (char *)malloc(1);\n result[0] = \'\\0\';\n return result;\n}\n\n\n\n```\n```Java []\n\nclass Solution {\n public String longestPalindrome(String s) {\n for (int length = s.length(); length > 0; length--) {\n for (int start = 0; start <= s.length() - length; start++) {\n if (check(start, start + length, s)) {\n return s.substring(start, start + length);\n }\n }\n }\n \n return "";\n }\n \n private boolean check(int i, int j, String s) {\n int left = i;\n int right = j - 1;\n \n while (left < right) {\n if (s.charAt(left) != s.charAt(right)) {\n return false;\n }\n \n left++;\n right--;\n }\n \n return true;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n def check(i, j):\n left = i\n right = j - 1\n \n while left < right:\n if s[left] != s[right]:\n return False\n \n left += 1\n right -= 1\n \n return True\n \n for length in range(len(s), 0, -1):\n for start in range(len(s) - length + 1):\n if check(start, start + length):\n return s[start:start + length]\n\n return ""\n\n\n```\n```javascript []\nvar longestPalindrome = function (s) {\n function check(i, j, s) {\n let left = i;\n let right = j - 1;\n \n while (left < right) {\n if (s[left] !== s[right]) {\n return false;\n }\n \n left++;\n right--;\n }\n \n return true;\n }\n\n for (let length = s.length; length > 0; length--) {\n for (let start = 0; start <= s.length - length; start++) {\n if (check(start, start + length, s)) {\n return s.substring(start, start + length);\n }\n }\n }\n\n return "";\n};\n\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log(result); // Output: "bab" or "aba"\n\n```\n\n\n---\n\n#### ***Approach 2(DP)***\n1. The `longestPalindrome` function is the main function for finding the longest palindromic substring.\n\n1. It initializes a vector `ans` to store the indices of the start and end of the longest palindrome found. Initially, it\'s set to {0, 0}, indicating no palindrome.\n\n1. The code iterates through each character in the input string `s` using a for loop with index `i`.\n\n1. Inside the loop, it first finds the length of the longest odd-length palindrome centered at the current character `i`. It does this by calling the `expand` function with the same `i` for both `left` and `right` indices. If this odd-length palindrome is longer than the previously found palindrome, it updates the `ans` vector with the new indices.\n\n1. Next, it finds the length of the longest even-length palindrome centered at the current character `i` and the next character `i+1`. It does this by calling the `expand` function with `i` and `i+1` as `left` and `right`. If this even-length palindrome is longer than the previously found palindrome, it updates the `ans` vector with the new indices.\n\n1. The code continues iterating through the string, updating `ans` as it finds longer palindromes.\n\n1. After the loop, the `i` and `j` values in the `ans` vector represent the start and end indices of the longest palindrome.\n\n1. Finally, it returns the longest palindrome by using the `substr` function to extract the substring from the input string s using the start and end indices.\n\n1. The `expand` function is a helper function that takes indices `i` and `j` and the input string `s` and returns the length of the palindrome that can be expanded from these indices. It expands the palindrome by moving the `left` and `right` indices towards the center until they no longer match or reach the string boundaries. The length of the palindrome is determined by the difference between `right` and `left`, minus 1, since it includes both `i` and `j`.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(n^2)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n string longestPalindrome(string s) {\n vector<int> ans = {0, 0};\n\n for (int i = 0; i < s.length(); i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int i = ans[0];\n int j = ans[1];\n return s.substr(i, j - i + 1);\n }\n\nprivate:\n int expand(int i, int j, string s) {\n int left = i;\n int right = j;\n\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n }\n};\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n#include <string.h>\n\nchar *longestPalindrome(char *s) {\n int n = strlen(s);\n int ans[2] = {0, 0};\n\n for (int i = 0; i < n; i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int start = ans[0];\n int end = ans[1];\n char *result = (char *)malloc((end - start + 2) * sizeof(char));\n strncpy(result, s + start, end - start + 1);\n result[end - start + 1] = \'\\0\';\n return result;\n}\n\nint expand(int i, int j, char *s) {\n int left = i;\n int right = j;\n\n while (left >= 0 && right < strlen(s) && s[left] == s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n}\n\nint main() {\n char s[] = "babad";\n char *result = longestPalindrome(s);\n printf("%s\\n", result); // Output: "bab" or "aba"\n free(result);\n return 0;\n}\n\n\n\n```\n```Java []\n\nclass Solution {\n public String longestPalindrome(String s) {\n int n = s.length();\n boolean[][] dp = new boolean[n][n];\n int[] ans = new int[]{0, 0};\n \n for (int i = 0; i < n; i++) {\n dp[i][i] = true;\n }\n \n for (int i = 0; i < n - 1; i++) {\n if (s.charAt(i) == s.charAt(i + 1)) {\n dp[i][i + 1] = true;\n ans[0] = i;\n ans[1] = i + 1;\n }\n }\n \n for (int diff = 2; diff < n; diff++) {\n for (int i = 0; i < n - diff; i++) {\n int j = i + diff;\n if (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {\n dp[i][j] = true;\n ans[0] = i;\n ans[1] = j;\n }\n }\n }\n \n int i = ans[0];\n int j = ans[1];\n return s.substring(i, j + 1);\n }\n}\n\n```\n```python3 []\n\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n n = len(s)\n dp = [[False] * n for _ in range(n)]\n ans = [0, 0]\n \n for i in range(n):\n dp[i][i] = True\n \n for i in range(n - 1):\n if s[i] == s[i + 1]:\n dp[i][i + 1] = True\n ans = [i, i + 1]\n\n for diff in range(2, n):\n for i in range(n - diff):\n j = i + diff\n if s[i] == s[j] and dp[i + 1][j - 1]:\n dp[i][j] = True\n ans = [i, j]\n\n i, j = ans\n return s[i:j + 1]\n\n```\n```javascript []\nvar longestPalindrome = function (s) {\n let ans = [0, 0];\n\n for (let i = 0; i < s.length; i++) {\n let oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n let dist = Math.floor(oddLength / 2);\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n let evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n let dist = Math.floor(evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n let start = ans[0];\n let end = ans[1];\n return s.slice(start, end + 1);\n};\n\nfunction expand(i, j, s) {\n let left = i;\n let right = j;\n\n while (left >= 0 && right < s.length && s[left] === s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n}\n\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log(result); // Output: "bab" or "aba"\n\n```\n\n\n---\n#### ***Approach 3(Expand From Center)***\n1. The `longestPalindrome` function is the main function for finding the longest palindromic substring.\n\n1. It initializes a vector `ans` to store the indices of the start and end of the longest palindrome found. Initially, it\'s set to {0, 0}, indicating no palindrome.\n\n1. The code iterates through each character in the input string `s` using a for loop with index `i`.\n\n1. Inside the loop, it first finds the length of the longest odd-length palindrome centered at the current character `i`. It does this by calling the `expand` function with the same `i` for both `left` and `right` indices. If this odd-length palindrome is longer than the previously found palindrome, it updates the `ans` vector with the new indices.\n\n1. Next, it finds the length of the longest even-length palindrome centered at the current character `i` and the next character `i+1`. It does this by calling the `expand` function with i and `i+1` as `left` and `right`. If this even-length palindrome is longer than the previously found palindrome, it updates the `ans` vector with the new indices.\n\n1. The code continues iterating through the string, updating `ans` as it finds longer palindromes.\n\n1. After the loop, the `start` and `end` values in the `ans` vector represent the start and end indices of the longest palindrome.\n\n1. Finally, it returns the longest palindrome by using the `substr` function to extract the substring from the input string `s` using the start and end indices. The length of the substring is calculated by subtracting the start index from the end index and adding 1 to include the character at the end.\n\n1. The `expand` function is a helper function that takes indices `i` and `j`, as well as the input string `s`, and returns the length of the palindrome that can be expanded from these indices. It expands the palindrome by moving the `left` and `right` indices towards the center until they no longer match or reach the string boundaries. The length of the palindrome is determined by the difference between `right` and `left`, minus 1, since it includes both `i` and `j`.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\n\n\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n std::vector<int> ans = {0, 0};\n\n for (int i = 0; i < s.length(); i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int start = ans[0];\n int end = ans[1];\n return s.substr(start, end - start + 1);\n }\n\nprivate:\n int expand(int i, int j, const std::string &s) {\n int left = i;\n int right = j;\n\n while (left >= 0 && right < s.length() && s[left] == s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n }\n};\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <string.h>\n#include <stdlib.h>\n\nint expand(int i, int j, const char *s) {\n int left = i;\n int right = j;\n\n while (left >= 0 && right < strlen(s) && s[left] == s[right]) {\n left--;\n right++;\n }\n\n return right - left - 1;\n}\n\nchar *longestPalindrome(char *s) {\n int ans[2] = {0, 0};\n\n for (int i = 0; i < strlen(s); i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int start = ans[0];\n int end = ans[1];\n int len = end - start + 1;\n char *result = (char *)malloc(len + 1);\n strncpy(result, s + start, len);\n result[len] = \'\\0\';\n return result;\n}\n\n\n\n```\n```Java []\nclass Solution {\n public String longestPalindrome(String s) {\n int[] ans = new int[]{0, 0};\n \n for (int i = 0; i < s.length(); i++) {\n int oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n int dist = oddLength / 2;\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n \n int evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n int dist = (evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n int i = ans[0];\n int j = ans[1];\n return s.substring(i, j + 1);\n }\n \n private int expand(int i, int j, String s) {\n int left = i;\n int right = j;\n \n while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {\n left--;\n right++;\n }\n\n return right - left - 1;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n def expand(i, j):\n left = i\n right = j\n \n while left >= 0 and right < len(s) and s[left] == s[right]:\n left -= 1\n right += 1\n \n return right - left - 1\n \n ans = [0, 0]\n\n for i in range(len(s)):\n odd_length = expand(i, i)\n if odd_length > ans[1] - ans[0] + 1:\n dist = odd_length // 2\n ans = [i - dist, i + dist]\n\n even_length = expand(i, i + 1)\n if even_length > ans[1] - ans[0] + 1:\n dist = (even_length // 2) - 1\n ans = [i - dist, i + 1 + dist]\n \n i, j = ans\n return s[i:j + 1]\n\n\n```\n```javascript []\nvar longestPalindrome = function (s) {\n let ans = [0, 0];\n\n for (let i = 0; i < s.length; i++) {\n let oddLength = expand(i, i, s);\n if (oddLength > ans[1] - ans[0] + 1) {\n let dist = Math.floor(oddLength / 2);\n ans[0] = i - dist;\n ans[1] = i + dist;\n }\n\n let evenLength = expand(i, i + 1, s);\n if (evenLength > ans[1] - ans[0] + 1) {\n let dist = Math.floor(evenLength / 2) - 1;\n ans[0] = i - dist;\n ans[1] = i + 1 + dist;\n }\n }\n\n let start = ans[0];\n let end = ans[1];\n return s.substring(start, end + 1);\n};\n\nfunction expand(i, j, s) {\n let left = i;\n let right = j;\n\n while (left >= 0 && right < s.length && s.charAt(left) === s.charAt(right)) {\n left--;\n right++;\n }\n\n return right - left - 1;\n}\n\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log(result); // Output: "bab" or "aba"\n\n```\n\n\n---\n#### ***Approach 4(Manacher\'s Algorithm)***\n1. The `longestPalindrome` function is the main function for finding the longest palindromic substring.\n\n1. It first preprocesses the input string `s` to create a new string `sPrime` that contains `#` characters between each character of the original string. This is done to handle both even and odd length palindromes more uniformly.\n\n1. It calculates the length of `sPrime` and initializes a vector `palindromeRadii` with the same length. The `palindromeRadii` vector will store the lengths of the palindromes centered at each position in `sPrime`.\n\n1. The code initializes two variables, `center` and `radius`, to keep track of the center and right boundary of the rightmost known palindrome.\n\n1. It then enters a loop that iterates over each character in `sPrime` (and its corresponding position in the original `s`).\n\n1. For each character, it calculates a mirror index `mirror` with respect to the current `center`. If the current character is within the current palindrome (i.e., `i < radius`), it updates the `palindromeRadii` with the minimum of the distance from the right boundary and the corresponding mirror value.\n\n1. The code then attempts to expand the palindrome centered at the current character. It uses a while loop to compare characters symmetrically around the current position (with `i` as the center), extending the palindrome if the characters match. It increments `palindromeRadii[i]` accordingly.\n\n1. If the extended palindrome goes beyond the right boundary, it updates the `center` and `radius` to the current character.\n\n1. After processing all characters, the code finds the maximum value in the `palindromeRadii` vector, which represents the length of the longest palindrome. It also determines the index of the center of this longest palindrome.\n\n1. With the center index and the palindrome length, it calculates the start index of the palindrome within the original string `s`.\n\n1. Finally, it returns the longest palindromic substring by using the `substr` function to extract the substring from the original input string `s` using the calculated start index and palindrome length.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\n\n\nclass Solution {\npublic:\n std::string longestPalindrome(std::string s) {\n std::string sPrime = "#";\n for (char c : s) {\n sPrime += \'#\';\n sPrime.push_back(c);\n }\n sPrime += \'#\';\n\n int n = sPrime.length();\n std::vector<int> palindromeRadii(n, 0);\n int center = 0;\n int radius = 0;\n\n for (int i = 0; i < n; i++) {\n int mirror = 2 * center - i;\n\n if (i < radius) {\n palindromeRadii[i] = std::min(radius - i, palindromeRadii[mirror]);\n }\n\n while (i + 1 + palindromeRadii[i] < n &&\n i - 1 - palindromeRadii[i] >= 0 &&\n sPrime[i + 1 + palindromeRadii[i]] == sPrime[i - 1 - palindromeRadii[i]]) {\n palindromeRadii[i]++;\n }\n\n if (i + palindromeRadii[i] > radius) {\n center = i;\n radius = i + palindromeRadii[i];\n }\n }\n\n int maxLength = *std::max_element(palindromeRadii.begin(), palindromeRadii.end());\n int centerIndex = std::distance(palindromeRadii.begin(), std::max_element(palindromeRadii.begin(), palindromeRadii.end()));\n int startIndex = (centerIndex - maxLength) / 2;\n std::string longestPalindrome = s.substr(startIndex, maxLength);\n\n return longestPalindrome;\n }\n};\n\n```\n```C []\n\nchar* longestPalindrome(char* s) {\n int len = strlen(s);\n char sPrime[2 * len + 1];\n int k = 0;\n\n for (int i = 0; i < len; i++) {\n sPrime[k++] = \'#\';\n sPrime[k++] = s[i];\n }\n sPrime[k++] = \'#\';\n sPrime[k] = \'\\0\';\n\n int n = 2 * len + 1;\n int* palindromeRadii = (int*)malloc(n * sizeof(int));\n\n int center = 0;\n int radius = 0;\n\n for (int i = 0; i < n; i++) {\n int mirror = 2 * center - i;\n\n if (i < radius) {\n palindromeRadii[i] = (radius - i) < palindromeRadii[mirror] ? (radius - i) : palindromeRadii[mirror];\n }\n\n while (i + 1 + palindromeRadii[i] < n && i - 1 - palindromeRadii[i] >= 0 && sPrime[i + 1 + palindromeRadii[i]] == sPrime[i - 1 - palindromeRadii[i]]) {\n palindromeRadii[i]++;\n }\n\n if (i + palindromeRadii[i] > radius) {\n center = i;\n radius = i + palindromeRadii[i];\n }\n }\n\n int maxLength = 0;\n int centerIndex = 0;\n for (int i = 0; i < n; i++) {\n if (palindromeRadii[i] > maxLength) {\n maxLength = palindromeRadii[i];\n centerIndex = i;\n }\n }\n\n int startIndex = (centerIndex - maxLength) / 2;\n char* longestPalindrome = (char*)malloc((maxLength + 1) * sizeof(char));\n strncpy(longestPalindrome, s + startIndex, maxLength);\n longestPalindrome[maxLength] = \'\\0\';\n\n free(palindromeRadii);\n return longestPalindrome;\n}\n\n\n```\n```Java []\n\nclass Solution {\n public String longestPalindrome(String s) {\n StringBuilder sPrime = new StringBuilder("#");\n for (char c: s.toCharArray()) {\n sPrime.append(c).append("#");\n }\n \n int n = sPrime.length();\n int[] palindromeRadii = new int[n];\n int center = 0;\n int radius = 0;\n \n for (int i = 0; i < n; i++) {\n int mirror = 2 * center - i;\n \n if (i < radius) {\n palindromeRadii[i] = Math.min(radius - i, palindromeRadii[mirror]);\n }\n \n while (i + 1 + palindromeRadii[i] < n &&\n i - 1 - palindromeRadii[i] >= 0 &&\n sPrime.charAt(i + 1 + palindromeRadii[i]) == sPrime.charAt(i - 1 - palindromeRadii[i])) {\n palindromeRadii[i]++;\n }\n \n if (i + palindromeRadii[i] > radius) {\n center = i;\n radius = i + palindromeRadii[i];\n }\n }\n \n int maxLength = 0;\n int centerIndex = 0;\n for (int i = 0; i < n; i++) {\n if (palindromeRadii[i] > maxLength) {\n maxLength = palindromeRadii[i];\n centerIndex = i;\n }\n }\n \n int startIndex = (centerIndex - maxLength) / 2;\n String longestPalindrome = s.substring(startIndex, startIndex + maxLength);\n \n return longestPalindrome;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n s_prime = \'#\' + \'#\'.join(s) + \'#\'\n n = len(s_prime)\n palindrome_radii = [0] * n\n center = radius = 0\n \n for i in range(n):\n mirror = 2 * center - i\n\n if i < radius:\n palindrome_radii[i] = min(radius - i, palindrome_radii[mirror])\n\n while (i + 1 + palindrome_radii[i] < n and \n i - 1 - palindrome_radii[i] >= 0 and\n s_prime[i + 1 + palindrome_radii[i]] == s_prime[i - 1 - palindrome_radii[i]]):\n palindrome_radii[i] += 1\n\n if i + palindrome_radii[i] > radius:\n center = i\n radius = i + palindrome_radii[i]\n\n max_length = max(palindrome_radii)\n center_index = palindrome_radii.index(max_length)\n start_index = (center_index - max_length) // 2\n longest_palindrome = s[start_index: start_index + max_length]\n\n return longest_palindrome\n\n\n```\n```javascript []\nvar longestPalindrome = function (s) {\n let sPrime = \'#\';\n\n for (let i = 0; i < s.length; i++) {\n sPrime += \'#\';\n sPrime += s[i];\n }\n\n sPrime += \'#\';\n\n const n = sPrime.length;\n const palindromeRadii = new Array(n).fill(0);\n let center = 0;\n let radius = 0;\n\n for (let i = 0; i < n; i++) {\n const mirror = 2 * center - i;\n\n if (i < radius) {\n palindromeRadii[i] = Math.min(radius - i, palindromeRadii[mirror]);\n }\n\n while (i + 1 + palindromeRadii[i] < n &&\n i - 1 - palindromeRadii[i] >= 0 &&\n sPrime[i + 1 + palindromeRadii[i]] === sPrime[i - 1 - palindromeRadii[i]) {\n palindromeRadii[i]++;\n }\n\n if (i + palindromeRadii[i] > radius) {\n center = i;\n radius = i + palindromeRadii[i];\n }\n }\n\n let maxLength = 0;\n let centerIndex = 0;\n\n for (let i = 0; i < n; i++) {\n if (palindromeRadii[i] > maxLength) {\n maxLength = palindromeRadii[i];\n centerIndex = i;\n }\n }\n\n const startIndex = Math.floor((centerIndex - maxLength) / 2);\n return s.substring(startIndex, startIndex + maxLength);\n};\n\nconst s = "babad";\nconst result = longestPalindrome(s);\nconsole.log(result); // Output: "bab" or "aba"\n\n```\n\n\n---\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅ Python Solution | Dynamic Programming | longest-palindromic-substring | 0 | 1 | # Intuition\n- Using DP\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Using 2D list\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` Python3 []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n lens = len(s)\n dp = [[0]*lens for _ in range(lens)]\n for i in range(lens - 1):\n dp[i][i] = 1\n if (s[i] == s[i+1]):\n dp[i][i+1] = 2\n # dp[-1][-1] doesn\'t matter\n for j in range(2, lens):\n for i in range(lens-j):\n if dp[i+1][j-1] > 0 and s[i] == s[j]:\n dp[i][j] = dp[i+1][j-1] + 2\n j += 1\n # print(dp)\n maxv = 1\n maxi = 0\n maxj = 0\n for i in range(lens):\n for j in range(i, lens):\n if maxv < dp[i][j]:\n maxv = dp[i][j]\n maxi = i\n maxj = j\n return s[maxi:maxj+1]\n``` | 0 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
✅ Python Solution | Dynamic Programming | longest-palindromic-substring | 0 | 1 | # Intuition\n- Using DP\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Using 2D list\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` Python3 []\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n lens = len(s)\n dp = [[0]*lens for _ in range(lens)]\n for i in range(lens - 1):\n dp[i][i] = 1\n if (s[i] == s[i+1]):\n dp[i][i+1] = 2\n # dp[-1][-1] doesn\'t matter\n for j in range(2, lens):\n for i in range(lens-j):\n if dp[i+1][j-1] > 0 and s[i] == s[j]:\n dp[i][j] = dp[i+1][j-1] + 2\n j += 1\n # print(dp)\n maxv = 1\n maxi = 0\n maxj = 0\n for i in range(lens):\n for j in range(i, lens):\n if maxv < dp[i][j]:\n maxv = dp[i][j]\n maxi = i\n maxj = j\n return s[maxi:maxj+1]\n``` | 0 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
5. Longest Palindromic Substring | longest-palindromic-substring | 0 | 1 | # Intuition:\nTo find the longest palindromic substring, the approach considers expanding around each character in the given string `s` to find both odd and even-length palindromes. It aims to optimize the search process by comparing substrings around the potential centers.\n\n# Approach:\n1. Initialize `start` and `max_len` variables to track the starting index and length of the longest palindrome found.\n2. Iterate through the string, considering each character as a potential center of a palindrome.\n3. For each character, expand outward to check both odd and even-length palindromes.\n4. Update `start` and `max_len` when a longer palindrome is found.\n5. Return the longest palindromic substring.\n\n# Complexity:\n- Time complexity: O(n^2) where `n` is the length of the input string `s`. The nested loops iterate through each character in the string and expand outward to check palindromes.\n- Space complexity: O(1) as only constant extra space is used to store indices and lengths.\n\n# Code:\n\n```python\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) < 2 or s == s[::-1]:\n return s\n \n start, max_len = 0, 1\n\n for i in range(len(s)):\n odd = s[i - max_len - 1 : i + 1]\n even = s[i - max_len : i + 1]\n\n if i - max_len - 1 >= 0 and odd == odd[::-1]:\n start = i - max_len - 1\n max_len += 2\n elif i - max_len >= 0 and even == even[::-1]:\n start = i - max_len\n max_len += 1\n\n return s[start : start + max_len]\n```\n | 0 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
5. Longest Palindromic Substring | longest-palindromic-substring | 0 | 1 | # Intuition:\nTo find the longest palindromic substring, the approach considers expanding around each character in the given string `s` to find both odd and even-length palindromes. It aims to optimize the search process by comparing substrings around the potential centers.\n\n# Approach:\n1. Initialize `start` and `max_len` variables to track the starting index and length of the longest palindrome found.\n2. Iterate through the string, considering each character as a potential center of a palindrome.\n3. For each character, expand outward to check both odd and even-length palindromes.\n4. Update `start` and `max_len` when a longer palindrome is found.\n5. Return the longest palindromic substring.\n\n# Complexity:\n- Time complexity: O(n^2) where `n` is the length of the input string `s`. The nested loops iterate through each character in the string and expand outward to check palindromes.\n- Space complexity: O(1) as only constant extra space is used to store indices and lengths.\n\n# Code:\n\n```python\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n if len(s) < 2 or s == s[::-1]:\n return s\n \n start, max_len = 0, 1\n\n for i in range(len(s)):\n odd = s[i - max_len - 1 : i + 1]\n even = s[i - max_len : i + 1]\n\n if i - max_len - 1 >= 0 and odd == odd[::-1]:\n start = i - max_len - 1\n max_len += 2\n elif i - max_len >= 0 and even == even[::-1]:\n start = i - max_len\n max_len += 1\n\n return s[start : start + max_len]\n```\n | 0 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Commented and Readable Python Solution with O(1) Space | longest-palindromic-substring | 0 | 1 | ```\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n n=len(s)\n #for storing the maximum pallindromic substr length\n max_length=0\n begin=0\n end=0\n for i in range(n):\n #pallindromic string can be of two types odd or even \n \n #First we will look for even \n low=i-1\n high=i\n while low>=0 and high < n and s[low]==s[high]:\n #update your max_length and begin and end \n if high-low+1>max_length:\n max_length=high-low+1\n begin=low\n end=high\n #update low and high\n low-=1\n high+=1\n \n #Now we will look for odd length string\n low=i-1\n high=i+1\n while low>=0 and high < n and s[low]==s[high]:\n #update your max_length and begin and end \n if high-low+1>max_length:\n max_length=high-low+1\n begin=low\n end=high\n #update low and high\n low-=1\n high+=1\n #return the answer\n return s[begin:end+1]\n``` | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
Commented and Readable Python Solution with O(1) Space | longest-palindromic-substring | 0 | 1 | ```\nclass Solution:\n def longestPalindrome(self, s: str) -> str:\n n=len(s)\n #for storing the maximum pallindromic substr length\n max_length=0\n begin=0\n end=0\n for i in range(n):\n #pallindromic string can be of two types odd or even \n \n #First we will look for even \n low=i-1\n high=i\n while low>=0 and high < n and s[low]==s[high]:\n #update your max_length and begin and end \n if high-low+1>max_length:\n max_length=high-low+1\n begin=low\n end=high\n #update low and high\n low-=1\n high+=1\n \n #Now we will look for odd length string\n low=i-1\n high=i+1\n while low>=0 and high < n and s[low]==s[high]:\n #update your max_length and begin and end \n if high-low+1>max_length:\n max_length=high-low+1\n begin=low\n end=high\n #update low and high\n low-=1\n high+=1\n #return the answer\n return s[begin:end+1]\n``` | 1 | Given a string `s`, return _the longest_ _palindromic_ _substring_ in `s`.
**Example 1:**
**Input:** s = "babad "
**Output:** "bab "
**Explanation:** "aba " is also a valid answer.
**Example 2:**
**Input:** s = "cbbd "
**Output:** "bb "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consist of only digits and English letters. | How can we reuse a previously computed palindrome to compute a larger palindrome? If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome? Complexity based hint:
If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation. |
[VIDEO] Step-by-Step Visualization of O(n) Solution | zigzag-conversion | 0 | 1 | https://youtu.be/ytSl-K4xo3w\n\nThe key to solving this problem is to understand that we assign characters to rows by <i>oscillating</i> between the top and bottom rows. In other words, if we traversed the string and looked at which row each character belonged to (let\u2019s say numRows is 3), the pattern would be 1 2 3 2 1 2 3 2 1.. so the first character goes in row 1, the second character goes in rows 2, the third character goes in row 3 - which is the bottom row - so now you go back up to row 2, then row 1.\n\nTo represent the rows, we\u2019ll use a 2D array named `rows`, where each inner list represents a row. We then use a variable called `index` that will oscillate between the top and bottom rows and assign characters to rows.\n\nWe\u2019ll control the direction that index moves by using a variable called `step`. `step` will either be 1 or -1, where a value of 1 means we need to increment the index (so move DOWN a row) and a value of -1 means we need to decrement the index (move UP a row). Whenever we reach either the first or last row, we\'ll switch the direction to move `index` in the opposite direction.\n\nA common mistake I see is creating a 1D list and initializing an empty string for each row. Then, instead of appending to a list, each character is added by using string concatenation. While this works, this is not O(n) because strings are immutable. In other words, string concatenation allocates new memory and copies over each character from both strings to create an entirely new string. That means that the string concatenation runs in O(n), so the overall algorithm runs in O(n<sup>2</sup>) time.\n\nInstead, by using lists (since lists are mutable), appending to a list runs in constant time - or more precisely, the amortized complexity of appending to a list is constant. So that allows everything inside the loop to run in constant time, so the algorithm now runs in O(n) time. \n\n# Code\n```\nclass Solution(object):\n def convert(self, s, numRows):\n if numRows == 1 or numRows >= len(s):\n return s\n \n rows = [[] for row in range(numRows)]\n index = 0\n step = -1\n for char in s:\n rows[index].append(char)\n if index == 0:\n step = 1\n elif index == numRows - 1:\n step = -1\n index += step\n\n for i in range(numRows):\n rows[i] = \'\'.join(rows[i])\n return \'\'.join(rows)\n``` | 17 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
O(n) Solution with Approaches | zigzag-conversion | 0 | 1 | # Intuition\nFor the Row R and the zigzag N, the character need to be extract is s[R + N * (total number of characters in a zigzag)] and s[-R + (N + 1) * (total number of characters in a zigzag)]\n\n# Approach\n1 Calculate how many time the sigzag repeats(steps).\n2 Generate result string from the characters in the first row.\n3 Generate result string from the characters from the 2nd to second last rows.\n4 Genertate result string from the characters in the last row.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def convert(self, s: str, numRows: int) -> str:\n### Calculate how many time the sigzag repeats(steps).\n def calculate_steps(length, numRows):\n if (numRows * 2 - 2) > 0:\n steps = length // (numRows * 2 - 2)\n mod = length % (numRows * 2 - 2)\n else: \n steps = 0\n mod = length\n if mod > 0:\n steps += 1\n return steps\n\n if len(s) <= numRows or numRows == 1:\n return(s)\n\n steps = calculate_steps(len(s), numRows)\n res = ""\n\n pack = 2 * numRows - 2 #How many characters in a single sigzag\n\n### Generate result string from the characters in the first row.\n for step in range(steps):\n if pack * step < len(s):\n res += s[pack * step]\n \n### Generate result string from the characters from the 2nd to second last rows.\n for row in range(1, numRows-1):\n for step in range(steps):\n position1 = pack * step + row\n if position1 < len(s):\n res += s[position1]\n position2 = pack - row + pack * step\n if position2 <len(s):\n res += s[position2]\n### Genertate result string from the characters in the last row.\n for step in range(steps):\n position = pack * step + numRows - 1\n if position < len(s):\n res += s[position]\n return res\n\n\n \n``` | 2 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
ZigZag Conversion Decoded! 🔄✨ Code in C++, Java, Python, C#, JS 🚀 | zigzag-conversion | 1 | 1 | # \u2753ZigZag Conversion\u2753\n---\n\n## \uD83D\uDCA1Approach 1: ZigZag Pattern\n\n### \u2728Explanation\nThe solution utilizes the zigzag pattern to convert the input string. It initializes a vector of strings representing each row and iterates through the input string, placing characters in the corresponding rows based on the zigzag pattern.\n\n### \uD83D\uDCDDDry Run\nLet\'s take the example input "PAYPALISHIRING" with numRows = 3:\n```\nP A H N\nA P L S I I G\nY I R\n```\n\n#### Execution Steps:\n\n1. **Initialization:**\n - `rows`: ["", "", ""]\n - `direction`: -1\n - `idx`: 0\n\n2. **Iterative Placement:**\n - Process characters one by one and place them in the corresponding rows.\n - Adjust the row index based on the zigzag pattern.\n\n3. **Resultant `rows`:**\n - ["PAHN", "APLSIIG", "YIR"]\n\n4. **Combining Rows:**\n - Concatenate the rows to obtain the final result: "PAHNAPLSIIGYIR"\n\n### \uD83D\uDD78\uFE0F Complexity Analysis\n\n- **Time Complexity:** O(N), where N is the length of the input string.\n- **Space Complexity:** O(min(N, numRows)), as `rows` stores each row.\n\n\n## \uD83D\uDCA1 Additional Explanation\n\n### \uD83D\uDE80 Handling Single Row Case\n\nThe solution efficiently handles the case when numRows is 1. In such a scenario, the input string remains unchanged, and the original string is returned. This optimization improves the overall efficiency of the algorithm.\n\n\n### \uD83E\uDDD1\uD83C\uDFFB\u200D\uD83D\uDCBBCodes in (C++) (Java) (Python) (C#) (JavaScript)\n\n```cpp []\nclass Solution {\npublic:\n string convert(string inputString, int numRows) {\n // If there\'s only one row, return the string as it is\n if (numRows == 1) return inputString;\n \n vector<string> rows(min(numRows, int(inputString.size())), "");\n int direction = -1; // -1 represents down, 1 represents up\n int currentRow = 0;\n \n for (int i = 0; i < inputString.size(); i++) {\n rows[currentRow] += inputString[i];\n currentRow += (direction == -1) ? 1 : -1;\n \n // Change direction when reaching the first or last row\n if (currentRow == 0 || currentRow == numRows - 1) {\n direction = -direction;\n }\n }\n \n string result = "";\n for (const auto& row : rows) {\n result += row;\n }\n \n return result;\n }\n};\n```\n\n```java []\n// Java code block for the approach\nclass Solution {\n public String convert(String inputString, int numRows) {\n if (numRows == 1) return inputString;\n\n List<StringBuilder> rows = new ArrayList<>();\n for (int i = 0; i < Math.min(numRows, inputString.length()); i++) {\n rows.add(new StringBuilder());\n }\n\n int direction = -1;\n int currentRow = 0;\n\n for (char c : inputString.toCharArray()) {\n rows.get(currentRow).append(c);\n currentRow += (direction == -1) ? 1 : -1;\n\n if (currentRow == 0 || currentRow == numRows - 1) {\n direction = -direction;\n }\n }\n\n StringBuilder result = new StringBuilder();\n for (StringBuilder row : rows) {\n result.append(row);\n }\n\n return result.toString();\n }\n}\n```\n\n```python []\n# Python code block for the approach\nclass Solution:\n def convert(self, inputString: str, numRows: int) -> str:\n if numRows == 1:\n return inputString\n\n rows = [\'\'] * min(numRows, len(inputString))\n direction, current_row = -1, 0\n\n for char in inputString:\n rows[current_row] += char\n current_row += 1 if direction == -1 else -1\n\n if current_row == 0 or current_row == numRows - 1:\n direction = -direction\n\n return \'\'.join(rows)\n```\n\n```csharp []\n// C# code block for the approach\npublic class Solution {\n public string Convert(string inputString, int numRows) {\n if (numRows == 1) return inputString;\n\n List<StringBuilder> rows = new List<StringBuilder>(Math.Min(numRows, inputString.Length));\n for (int i = 0; i < Math.Min(numRows, inputString.Length); i++) {\n rows.Add(new StringBuilder());\n }\n\n int direction = -1;\n int currentRow = 0;\n\n foreach (char c in inputString) {\n rows[currentRow].Append(c);\n currentRow += (direction == -1) ? 1 : -1;\n\n if (currentRow == 0 || currentRow == numRows - 1) {\n direction = -direction;\n }\n }\n\n StringBuilder result = new StringBuilder();\n foreach (StringBuilder row in rows) {\n result.Append(row);\n }\n\n return result.ToString();\n }\n}\n```\n\n```javascript []\n// JavaScript code block for the approach\n\n var convert = function(inputString, numRows) {\n if (numRows === 1) return inputString;\n\n const rows = new Array(Math.min(numRows, inputString.length)).fill(\'\');\n let direction = -1;\n let currentRow = 0;\n\n for (const char of inputString) {\n rows[currentRow] += char;\n currentRow += (direction === -1) ? 1 : -1;\n\n if (currentRow === 0 || currentRow === numRows - 1) {\n direction = -direction;\n }\n }\n\n return rows.join(\'\');\n }\n\n```\n---\n## \uD83D\uDCCA Analysis\n\n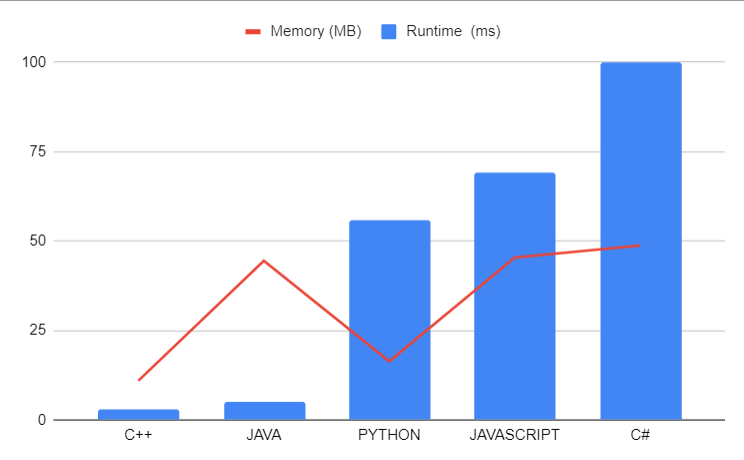\n\n| Language | Runtime (ms) | Memory (MB) |\n|-------------|--------------|-------------|\n| C++ | 3 | 11 |\n| JAVA | 5 | 44.5 |\n| PYTHON | 56 | 16.4 |\n| JAVASCRIPT | 69 | 45.4 |\n| C# | 100 | 48.8 |\n\n\n---\n\n## \uD83D\uDCAF Related Questions and Practice\n- [Spiral Matrix](https://leetcode.com/problems/spiral-matrix/description/)\n- [Spiral Matrix II](https://leetcode.com/problems/spiral-matrix-ii/description/)\n---\n\n# Consider UPVOTING\u2B06\uFE0F\n\n\n\n# DROP YOUR SUGGESTIONS IN THE COMMENT\n\n## Keep Coding\uD83E\uDDD1\u200D\uD83D\uDCBB\n\n -- *MR.ROBOT SIGNING OFF* | 2 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
Easy Explanation with Pics and Video | Java C++ Python | zigzag-conversion | 1 | 1 | \n\n\nThings become clear with the above image.\n\n# Intuition:\n1. Just look at the top row what is the difference b/w each char i.e A and I and I and Q = 8\n 5*2-2 == numberOf rows *2 - 2 (The corner elements are excluded).\nSimilarly for each row i.e B and J the diff is 8, C and K is 8\n2. The interesting part comes when the char in the diagnoal has to be added, but even this has a pattern\n\t\n\tThere will be no char in between for row 0 and row n.\n\tThere can be only one diagonal char and the diagonal diff is original diff -2 at each step or diff - (rowNumber*2);\n\n# Approach\n\n1. Create an empty StringBuilder which is our ans.\n2. Calculate the diff = numRows*2 -2;\n3. Iterate over 0 to rowNumber in a for loop \nThe first char will be row number or i (append to String)\n4. Write a while loop in the above for loop :\n5. The first char will be row number or i (append to String)\n6. Calculate the diagonalDiff if any and append to the String.\n7. Increase the index by diff and return ans.\n\n\nhttps://youtu.be/YwU8pENP-vw\n# If you find this useful\n\n\n```\nclass Solution {\n public String convert(String s, int numRows) {\n if (numRows == 1) {\n return s;\n }\n \n StringBuilder answer = new StringBuilder();\n int n = s.length();\n int diff = 2 * (numRows - 1);\n int diagonalDiff = diff;\n int secondIndex;\n int index;\n for (int i = 0; i < numRows; i++) {\n index = i;\n\n while (index < n) {\n answer.append(s.charAt(index));\n if (i != 0 && i != numRows - 1) {\n diagonalDiff = diff-2*i;\n secondIndex = index + diagonalDiff;\n \n if (secondIndex < n) {\n answer.append(s.charAt(secondIndex));\n }\n }\n index += diff;\n }\n }\n \n return answer.toString();\n }\n}\n```\n\n```\nclass Solution {\npublic:\n string convert(string s, int numRows) {\n if (numRows == 1) {\n return s;\n }\n \n stringstream answer;\n int n = s.length();\n int diff = 2 * (numRows - 1);\n int diagonalDiff = diff;\n int secondIndex;\n int index;\n for (int i = 0; i < numRows; i++) {\n index = i;\n\n while (index < n) {\n answer << s[index];\n if (i != 0 && i != numRows - 1) {\n diagonalDiff = diff-2*i;\n secondIndex = index + diagonalDiff;\n \n if (secondIndex < n) {\n answer << s[secondIndex];\n }\n }\n index += diff;\n }\n }\n \n return answer.str();\n }\n};\n\n```\n\n```\nclass Solution:\n def convert(self, s: str, numRows: int) -> str:\n if numRows == 1:\n return s\n answer = \'\'\n n = len(s)\n diff = 2 * (numRows - 1)\n diagonal_diff = diff\n second_index = 0\n index = 0\n for i in range(numRows):\n index = i\n while index < n:\n answer += s[index]\n if i != 0 and i != numRows - 1:\n diagonal_diff = diff - 2 * i\n second_index = index + diagonal_diff\n if second_index < n:\n answer += s[second_index]\n index += diff\n return answer\n```\n | 96 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
6. Zigzag Conversion || Solution for Python3 | zigzag-conversion | 0 | 1 | ```\nclass Solution:\n def convert(self, s: str, numRows: int) -> str:\n res, unit = "", numRows * 2 - 2\n if numRows == 1:\n return s \n for r in range(numRows):\n for n in range(len(s)):\n if r == 0 or r == numRows - 1:\n if unit * n + r < len(s):\n res += s[unit * n + r]\n else:\n if unit * n + r < len(s):\n res += s[unit * n + r]\n if unit * n + unit - r < len(s):\n res += s[unit * n + unit - r]\n return res\n```\n# Hard to understand? The explanation is here!\n1. The method initializes an empty string res which will store the converted result.\n\n2. It calculates the variable unit as numRows * 2 - 2. This is the number of characters in each "unit" of the zigzag pattern, consisting of a vertical line and a diagonal line.\n\n3. If numRows is equal to 1, the method returns the original string s as there would be no zigzag pattern to create.\n\n4. The method then enters a nested loop. The outer loop iterates through each row r in the range from 0 to numRows - 1.\n\n5. The inner loop iterates through each character n in the input string s.\n\n6. Inside the loops, the code checks whether the current row r is either the first row (0) or the last row (numRows - 1). If so, it appends the character at index unit * n + r to the res string.\n\n7. If the current row r is not the first or last row, the code appends two characters to the res string. The first character is from index unit * n + r, and the second character is from index unit * n + unit - r. This simulates the diagonal line in the zigzag pattern.\n\n8. The method continues looping through all rows and characters in the input string until the zigzag pattern is completely formed.\n\n9. Finally, the method returns the res string, which now contains the input string s converted into the zigzag pattern.\n\n# **Please Upvote!** | 2 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
Simple O(n) Python Solution for Zigzag Strings | zigzag-conversion | 0 | 1 | # Intuition\nThink of it like bouncing a ball: it goes down, hits the floor, and bounces back up. This is like our zigzag pattern with the string.\n\n# Approach\n1. If we only have one row or more rows than letters, just give back the original word.\n2. I used a jump thing to know if I should go up or down. If I\'m at the top, I\'ll go down. If I\'m at the bottom, I\'ll go up.\n3. For each letter in the word, I put it in the right row and then decide if I should move up or down next.\n4. After placing all the letters, I put all the rows together for the final word.\n\n# Complexity\n- Time complexity:\nIt\'s pretty quick. It goes through the word once, so $$O(n)$$.\n\n- Space complexity:\nI saved space. I only made room for the letters in the word, so $$O(n)$$ space.\n\n# Code\n```\nclass Solution(object):\n def convert(self, s, numRows):\n """\n :type s: str\n :type numRows: int\n :rtype: str\n """\n if numRows == 1 or numRows >= len(s):\n return s\n result = [\'\'] * numRows\n row, jump = 0, 1\n\n for char in s:\n result[row] += char\n if row == 0:\n jump = 1\n elif row == numRows - 1:\n jump = -1\n row += jump\n \n return \'\'.join(result)\n``` | 7 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
Python3 50ms 🔥very simple solution: Detailed Explained🔥🔥🔥 | zigzag-conversion | 0 | 1 | # Intuition\n****\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Zig-zag traversal is simple level order string traversal.**\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- we have to travers in level order, and our $$level-threshold$$ is $$numRows$$.\n- travers over $$length-of-string$$ and initial level is $$0$$.\n- increment level by 1 in each iteration\n- if we reach at last level according to numRows then $$traverse backwards$$ and decrement level by 1.\n- put current alphabet from string s to it\'s respective level\n- this all operation happens in $$O(n)$$ times.\n- now $$concatenate-all-characters$$ from level array and return, this also happens in $$O(n)$$ time.\n# Complexity\n- Time complexity: $$O(2n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n+c)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def convert(self, s: str, numRows: int) -> str:\n if numRows == 1:\n return s\n ans = [[] for _ in range(numRows)]\n level = 0\n answer = ""\n forward = True\n for i in range(len(s)):\n ans[level].append(s[i])\n if forward:\n level += 1\n if not forward:\n level -= 1\n if level > numRows - 1:\n level -= 2\n forward = False\n if level < 0:\n level += 2\n forward = True\n for i in ans:\n for j in i:\n answer += j\n return answer\n``` | 4 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
Python code : 59ms beats(86.35%) : with brief explanation | zigzag-conversion | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo create a 2d list with number of sublists equal to that of numRows where each sublist contains the letter from each rows of the input respectively.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nbasically we take each and every letter in the string and verify its positon using the move variable and place in the appropriate sublist\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def convert(self, s: str, numRows: int) -> str:\n z=len(s)\n g=0\n move=0\n ls=[]\n k=0\n while k<len(s):\n if g==0:\n move+=1\n\n else:\n move-=1\n\n if move==numRows:\n g=1\n\n elif move<=1:\n g=0 \n\n if k<numRows:\n ls.append([s[k]])\n\n \n else:\n ls[move-1].append(s[k]) \n\n k+=1\n\n word="" \n for i in ls:\n word+="".join(i)\n return word\n\n``` | 3 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
Very simple and intuitive O(n) python solution with explanation | zigzag-conversion | 0 | 1 | In this question the most important thing is getting the pattern correct. It is very easy to go down the wrong path and spend 10 minutes trying to figure out how to make a complicated algorithm work when a very easy one would suffice.\n\n> Thinking process\n\n1. First I looked at the problem and thought about how the printed pattern looked like it would be mapped out on a matrix. I wrote out the number of "main" columns and then the number of "middle" columns\n ```\n P I N\n A L S I G\n Y A H R\n P I\n ------------------------\n 4 2 4 2 2(*)\n ``` \n The last line is 2 only because the word ends, but we can see that the pattern is `4-2-4-2-4-...`. When drawing it out for `numRows = 3`, the pattern became \n\n ```\n P A H N\n A P L S I I G\n Y I R\n ---------------------------------\n 3 1 3 1 3 1 2(*)\n ``` \n Again we can see the pattern is `3-1-3-1-3-...`\n\n So the pattern of "main" rows to "mid" rows is `n, n-2, n, n-2, ...`\n\n When I tried to build an algorithm for this pattern I got stuck. How would I make the index move up `n`, then down `n-2` without confusing myself or missing edge cases?\n2. Next I tried to write out the row of each letter in the string. For numRows = 4, it became:\n ```\n P A Y P A L I S H I R I N G\n -----------------------------------------\n 1 2 3 4 3 2 1 2 3 4 3 2 1 2\n ```\n For numRows = 3, it became:\n ```\n P A Y P A L I S H I R I N G\n -----------------------------------------\n 1 2 3 2 1 2 3 2 1 2 3 2 1 2\n ```\n\n This is where I found the correct pattern. Basically instead of worrying about "main" rows vs. "mid" rows, it easily maps into moving the index from 1 -> numRows, and then from numRows -> 1. We don\'t even need to think about a matrix and worrying about rows vs. columns.\n\n> Algorithm\n\nAt first I thought about how to make the different rows as strings. How would I make `row1`, `row2`, `row3`? Sure if there were only a few rows I could hardcode them, but then how would I be able to add the character to each row easily? It is too difficult, so I thought using an array would be much better. \n\nThen I thought how would we make sure that we are going up and down in the correct pattern? The easiest way was to use a `going_up` flag to make sure to switch the direction of the index.\n\nLastly the only thing to check was edge cases, which by this point was pretty easy with a simple run through of the algorithm.\n\n> Code:\n\n```py\nclass Solution:\n def convert(self, s: str, numRows: int) -> str:\n if numRows == 1:\n return s\n \n row_arr = [""] * numRows\n row_idx = 1\n going_up = True\n\n for ch in s:\n row_arr[row_idx-1] += ch\n if row_idx == numRows:\n going_up = False\n elif row_idx == 1:\n going_up = True\n \n if going_up:\n row_idx += 1\n else:\n row_idx -= 1\n \n return "".join(row_arr)\n```\n\n> Time & Space Complexity\n\nTime: `O(n)`\n- We run through the whole string once: `O(n)`\n - everything we do inside the for loop: `O(1)`\n- Finally we join the whole array int a string: `O(n)`\n\nSpace: `O(n)`\n- We are creating a new array: `O(n)`\n- We are using join to put it back into a string: `O(n)` | 171 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
100 % ✔️ Solution Explained with visualization to the code | zigzag-conversion | 1 | 1 | [https://youtu.be/EWZWiG750FI]() | 51 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |
Python | well Explanation | Simple | Easy ✅✅ | zigzag-conversion | 0 | 1 | \nI solved this problem using index of each character in string `s`\n### The first and last rows:\nI find sequence of numbers that, each element is greater than the one before it by 6 (add) `2*numRows - 2`,\n### The others rows:\nThere are two numbers, the difference between them is fixed and repeated every `numRows`,\nThe first number, like the one I mentioned before, is greater than the one before it by 6 (add) `2*numRows - 2`.\nThe second is greater than the first by this equation: `index = j + add - 2*i`, `j: index of character`, `i: number of row`.\nAnd then I add every character using these equations in string `word` \n\n# Code\n```\nclass Solution(object):\n def convert(self, s, numRows):\n """\n :type s: str\n :type numRows: int\n :rtype: str\n """\n if numRows == 1:\n return s\n word = ""\n add = 2*numRows - 2\n n = len(s)\n for i in range(numRows):\n if i == 0 or i == numRows-1:\n for j in range(i,n,add):\n word += s[j]\n else:\n for j in range(i,n,add):\n word += s[j]\n index = j + add - 2*i\n if index < n:\n word += s[index]\n \n return word\n``` | 4 | The string `"PAYPALISHIRING "` is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: `"PAHNAPLSIIGYIR "`
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
**Example 1:**
**Input:** s = "PAYPALISHIRING ", numRows = 3
**Output:** "PAHNAPLSIIGYIR "
**Example 2:**
**Input:** s = "PAYPALISHIRING ", numRows = 4
**Output:** "PINALSIGYAHRPI "
**Explanation:**
P I N
A L S I G
Y A H R
P I
**Example 3:**
**Input:** s = "A ", numRows = 1
**Output:** "A "
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of English letters (lower-case and upper-case), `','` and `'.'`.
* `1 <= numRows <= 1000` | null |