Datasets:

ecnu-icalk

/

cmm-math

like 3

18306

["9076.jpg"]

C

null

高二

《九章算术》是我国古代数学成就的杰出代表作, 其中《方田》章给出计算弧田面积所用的经验方式为: 弧田面积 $=\frac{1}{2}$ (弦 $\times$ 矢+矢 ${ }^{2}$ ), 弧田（如图）由圆弧和其所对弦所围成, 公式中“弦”指圆弧所对弦长, “矢”等于半径长与圆心到弦的距离之差, 现有圆心角为 $\frac{2 \pi}{3}$, 半径等于 4 米的弧田, 按照上述经验公式计算所得弧田面积约是（）（ $\sqrt{3} \approx 1.73 ）$ <ImageHere>

A. 15 平方米 B. 12 平方米 C. 9 平方米 D. 6 平方米

度量几何学

如图,根据题意可得: $\angle A O B=\frac{2 \pi}{3}, O A=4$, 在 Rt $\triangle A O D$ 中, 可得: $\angle A O D=\frac{\pi}{3}, \angle D A O=\frac{\pi}{6}$, $O D=\frac{1}{2} A O=\frac{1}{2} \times 4=2$, 可得: 矢 $=4-2=2$, 由 $A D=A O \cdot \sin \frac{\pi}{3}=4 \times \frac{\sqrt{3}}{2}=2 \sqrt{3}$, 可得:弦 $=2 A D=2 \times 2 \sqrt{3}=4 \sqrt{3}$, 所以:弧田面积 $=\frac{1}{2}$ (弦 $\times$ 矢 $\div$ 矢 $\left.^{2}\right)=\frac{1}{2}\left(4 \sqrt{3} \times 2+2^{2}\right)=4 \sqrt{3}+2 \approx 9$ 平方米.所以 $\mathrm{C}$ 选项是正确的.

18308

["9077.jpg", "9078.jpg", "9079.jpg", "9080.jpg"]

C

null

高二

集合 $\left\{\alpha \left\lvert\, k \pi+\frac{\pi}{4} \leq \alpha \leq k \pi+\frac{\pi}{2}\right., k \in Z\right\}$ 中角所表示的范围(阴影部分)是(

A.<ImageHere> B.<ImageHere> C.<ImageHere> D.<ImageHere>

度量几何学

由集合 $\left\{\alpha \left\lvert\, k \pi+\frac{\pi}{4} \leq \alpha \leq k \pi+\frac{\pi}{2}\right., k \in Z\right\}$ ， 当 $k$ 为偶数时, 集合 $\left\{\alpha \left\lvert\, k \pi+\frac{\pi}{4} \leq \alpha \leq k \pi+\frac{\pi}{2}\right., k \in Z\right\}$ 与 $\left\{\alpha \left\lvert\, \frac{\pi}{4} \leq \alpha \leq \frac{\pi}{2}\right.\right\}$ 表示相同的角, 位于第一象限; 当 $k$ 为奇数时, 集合 $\left\{\alpha \left\lvert\, k \pi+\frac{\pi}{4} \leq \alpha \leq k \pi+\frac{\pi}{2}\right., k \in Z\right\}$ 与 $\left\{\alpha \left\lvert\, \frac{5 \pi}{4} \leq \alpha \leq \frac{3 \pi}{2}\right.\right\}$ 表示相同的角, 位于第三象限; 所以集合 $\left\{\alpha \left\lvert\, k \pi+\frac{\pi}{4} \leq \alpha \leq k \pi+\frac{\pi}{2}\right., k \in Z\right\}$ 中表示的角的范围为选项 C, 故选 C.

18309

[]

B

null

高二

下列各角中与角 $\frac{\pi}{3}$ 终边相同的是

A. $-\frac{\pi}{3}$ B. $-300^{\circ}$ C. $\frac{2 \pi}{3}$ D. $240^{\circ}$

度量几何学

与角 $\frac{\pi}{3}$ 终边相同的角 $\alpha=\frac{\pi}{3}+2 k \pi, k \in Z$, 当 $k=-1, \alpha=-\frac{5 \pi}{3}$, 即 $-300^{\circ}$, 选 $\mathrm{B}$

18310

[]

D

null

高二

一个半径为 $\mathbf{R}$ 的扇形, 它的周长为 $4 \mathrm{R}$, 则这个扇形所含弓形的面积为 ( )

A. $\frac{1}{2}(2-\sin 1 \cos 1) R^{2}$ B. $\frac{1}{2} \sin 1 \cos 1 R^{2}$ $\mathrm{C} \cdot \frac{1}{2} \mathrm{R}^{2}$ D. $(1-\sin 1 \cos 1) R^{2}$

度量几何学

一个半径为 $\mathrm{R}$ 的扇形, 它的周长为 $4 \mathrm{R}$, 则弧长为 $4 \mathrm{R}-2 \mathrm{R}=2 \mathrm{R}$, 扇形面积为 $\frac{1}{2} \times R \times 2 R=R^{2}$, 所含圆心角为 $\frac{2 R}{R}=2 \mathrm{rad}$, 所含三角形面积为 $\frac{1}{2} \times 2 R \sin 1 \times R \cos 1=\sin 1 \cos 1 R^{2}$, 所以这个扇形所含弓形的面积为 $(1-\sin 1 \cos 1) \mathrm{R}^{2}$ 故选择 D

20225

[]

A

null

高二

“ $\alpha=\frac{\pi}{6}$ ” 是 “ $\cos 2 \alpha=\frac{1}{2}$ ” 的 ( )

A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件

度量几何学

解析： $\alpha=\frac{\pi}{6}, \cos 2 \alpha=\cos \frac{\pi}{3}=\frac{1}{2}$, 但 $\cos 2 \alpha=\frac{1}{2}$, 得 $2 \alpha=2 k \pi \pm \frac{\pi}{3}, k \in \mathbf{Z}$,则 $\alpha$ 可以不等于 $\frac{\pi}{6}$, 则 “ $\alpha=\frac{\pi}{6}$ ” 是 “ $\cos 2 \alpha=\frac{1}{2}$ ” 的充分而不必要条件. 答案 ：A

20249

[]

A

null

高二

定义在闭区间 $[a, b]$ 上的函数 $y=f(x)$ 有唯一的极值点 $x=x_{0}$,且 $y_{\text {极小值 }}=f\left(x_{0}\right)$, 则下列说法正确的是 $(\quad)$

A. 函数 $f(x)$ 有最小值 $f\left(x_{0}\right)$ B. 函数 $f(x)$ 有最小值, 但不一定是 $f\left(x_{0}\right)$ C. 函数 $f(x)$ 的最大值也可能是 $f\left(x_{0}\right)$ D. 函数 $f(x)$ 不一定有最小值

度量几何学

解析 ：函数 $f(x)$ 在闭区间 $[a, b]$ 上一定存在最大值和最小值, 又 $f(x)$ 有唯一的极小值 $f\left(x_{0}\right)$, 则 $f\left(x_{0}\right)$ 一定是最小值. 答案： A

20327

[]

C

null

高二

一木块沿某一斜面自由下滑, 测得下滑的水平距离 $s$ 与时间 $t$之间的函数关系为 $s=\frac{1}{8} t^{2}$, 则当 $t=2$ 时, 此木块在水平方向的瞬时速度为( )

A. 2 B. 1 C. $\frac{1}{2}$ D. $\frac{1}{4}$

度量几何学

C

18316

["9083.jpg"]

C

null

高二

已知 $\mathbf{O}, \mathbf{N}, \mathbf{P}$ 在 $\triangle A B C$ 所在平面内, 且 $|\overline{O A}|=|\overline{O B}|=|\overline{O C}|, \overline{N A}+\overline{N B}+\overline{N C}=0$, 且 $\overline{P A} \cdot \overline{P B}=\overline{P B} \cdot \overline{P C}=\overline{P C} \cdot \overline{P A}$, 则点 $\mathbf{O}, \mathbf{N}, \mathbf{P}$ 依次是 $\triangle A B C$ 的 () （注: 三角形的三条高线交于一点, 此点为三角型的垂心）

A. 重心外心垂心 B. 重心外心内心 C. 外心重心垂心 D. 外心重心内心

度量几何学

因为 $|\overrightarrow{O A}|=|\overrightarrow{O B}|=|\overrightarrow{O C}|$, 所以 $O$ 到定点 $A, B, C$ 的距离相等, 所以 $O$ 为 $\triangle A B C$ 的外心, 由 $\overrightarrow{N A}+\overrightarrow{N B}+\overrightarrow{N C}=0$, 则 $\overrightarrow{N A}+\overrightarrow{N B}=-\overrightarrow{N C}$, 取 $A B$ 的中点 $E$, 则 $\overrightarrow{N A}+\overrightarrow{N B}=-\overrightarrow{2 N E}=\overrightarrow{C N}$, 所以 $2|\overrightarrow{N E}|=|\overrightarrow{C N}|$, 所以 $N$ 是 $\triangle A B C$ 的重心; 由 $\overrightarrow{P A} \cdot \overrightarrow{P B}=\overrightarrow{P B} \cdot \overrightarrow{P C}=\overrightarrow{P C} \cdot \overrightarrow{P A}$, 得 $(\overrightarrow{P A}-\overrightarrow{P C}) \cdot \overrightarrow{P B}=0$,即 $\overrightarrow{A C} \cdot \overrightarrow{P B}=0$, 所以 $A C \perp P B$, 同理 $A B \perp P C$, 所以点 $P$ 为 $\triangle A B C$ 的垂心, 故选 C. <ImageHere>

18320

["9086.jpg"]

D

null

高二

如图所示,<ImageHere> 设 $P$ 为 $\triangle A B C$ 所在平面内的一点, 并且 $\overrightarrow{A P}=\frac{1}{4} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}$, 则 $\triangle B P C$ 与 $\triangle A B C$ 的面积之比等于 ( )

A. $\frac{2}{5}$ B. $\frac{3}{5}$ C. $\frac{3}{4}$ D. $\frac{1}{4}$

度量几何学

延长 $\mathrm{AP}$ 交 $\mathrm{BC}$ 于点 $\mathrm{D}$, 因为 $\mathrm{A} 、 \mathrm{P} 、 \mathrm{D}$ 三点共线, 所以 $\overrightarrow{C P}=m \overrightarrow{C A}+n \overrightarrow{C D}(m+n=1)$, 设 $\overrightarrow{C D}=k \overrightarrow{C B}$ 代入可得 $\overrightarrow{C P}=m \overrightarrow{C A}+n k \overrightarrow{C B}$ 即 $\overrightarrow{A P}-\overrightarrow{A C}=-m \overrightarrow{A C}+n k(\overrightarrow{A B}-\overrightarrow{A C}) \Rightarrow \overrightarrow{A P}=(1-m-n k) \overrightarrow{A C}+n k \overrightarrow{A B}$ 又因为 $\overrightarrow{A P}=\frac{1}{4} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}$, 即 $n k=\frac{1}{4}, 1-m-n k=\frac{1}{2}$, 且 $m+n=1$ 解得 $m=\frac{1}{4}, n=\frac{3}{4}$ 所以 $\overrightarrow{C P}=\frac{1}{4} \overrightarrow{C A}+\frac{3}{4} \overrightarrow{C D}$ 可得 $\overrightarrow{A D}=4 \overrightarrow{P D}$ 因为 $\triangle B P C$ 与 $\triangle A B C$ 有相同的底边, 所以面积之比就等于 $|\overrightarrow{D P}|$ 与 $|\overrightarrow{A D}|$ 之比 所以 $\triangle B P C$ 与 $\triangle A B C$ 的面积之比为 $\frac{1}{4}$ 故选 D

18326

["9089.jpg"]

D

null

高二

已知点 $P$ 为 $A B C$ 内一点, $\overrightarrow{P A}+2 \overrightarrow{P B}+3 \overrightarrow{P C}=\overrightarrow{0}$, 则 $\triangle A P B, \triangle A P C, \triangle B P C$ 的面积之比为 ( )

A. $9: 4: 1$ B. $1: 4: 9$ C. $1: 2: 3$ D. $3: 2: 1$

度量几何学

$\because \overrightarrow{P A}+2 \overrightarrow{P B}+3 \overrightarrow{P C}=0, \therefore \overrightarrow{P A}+\overrightarrow{P C}=-2 \overrightarrow{(P B}+\overrightarrow{P C})$, 如图:<ImageHere> $\because \overrightarrow{P A}+\overrightarrow{P C}=\overrightarrow{P D}=2 \overrightarrow{P F}, \overrightarrow{P B}+\overrightarrow{P C}=\overrightarrow{P E}=2 \overrightarrow{P G}$ $\therefore \overrightarrow{P F}=-2 \overrightarrow{P G}$, $\therefore F 、 P 、 G$ 三点共线, 且 $P F=2 P G, G F$ 为三角形 $A B C$ 的中位线 $\therefore \frac{S_{\triangle A P C}}{S_{\triangle B P C}}=\frac{\frac{1}{2} \times P C \times h_{1}}{\frac{1}{2} \times P C \times h_{2}}=\frac{h_{1}}{h_{2}}=\frac{P F}{P G}=2$ 而 $S_{\triangle A P B}=\frac{1}{2} S_{\triangle A B C}$ $\therefore \triangle A P B, \triangle A P C, \triangle B P C$ 的面积之比等于 $3: 2: 1$ 故选: $D$.

18337

[]

A

null

高二

已知 $|\overrightarrow{A B}|=10,|\overrightarrow{B C}|=7$, 则 $|\overrightarrow{A C}|$ 的取值范围是( )

A. $[3,17]$ B. $[3,17)$ C. $[3,10]$ D. $(3,10]$

度量几何学

$\because \overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{B C}, \therefore|\overrightarrow{A C}|=|\overrightarrow{A B}+\overrightarrow{B C}| \leq|\overrightarrow{A B}|+|\overrightarrow{B C}|=17,|\overrightarrow{A C}|=|\overrightarrow{A B}+\overrightarrow{B C}| \geq|\overrightarrow{A B}|-|\overrightarrow{B C}|=3$, $\therefore 3 \leq|\overrightarrow{A C}| \leq 17$.

18344

["9092.jpg"]

D

null

高二

如图, 在 $\triangle A B C$ 中, $A D$ 是 $B C$ 边上的中线, $F$ 是 $A D$ 上的一点, 且 $\frac{A F}{F D}=\frac{1}{4}$, 连接 $C F$ 并延长交 $A B$ 于 $E$, 则 $\frac{A E}{E B}$ 等于( ) <ImageHere>

A. $\frac{1}{10}$ B. $\frac{1}{3}$ C. $\frac{1}{5}$ D. $\frac{1}{8}$

度量几何学

设 $\overrightarrow{A B}=\boldsymbol{a}, \overrightarrow{A C}=\boldsymbol{b}, \frac{A E}{E B}=\lambda \therefore \frac{A F}{F D}=\frac{1}{4}$, $\therefore \overrightarrow{C F}=\overrightarrow{C A}+\overrightarrow{A F}=\overrightarrow{C A}+\frac{1}{5} \overrightarrow{A D}=\frac{1}{10}(\overrightarrow{A B}+\overrightarrow{A C})-\overrightarrow{A C}=\frac{1}{10} \overrightarrow{A B}-\frac{9}{10} \overrightarrow{A C}$ $=\frac{1}{10} \boldsymbol{a}-\frac{9}{10} \boldsymbol{b} \cdot \overrightarrow{C E}=\overrightarrow{C A}+\overrightarrow{A E}=\overrightarrow{C A}+\frac{\lambda}{1+\lambda} \overrightarrow{A B}=\frac{\lambda}{1+\lambda} \overrightarrow{A B}-\overrightarrow{A C}=\frac{\lambda}{1+\lambda} \boldsymbol{a}-\boldsymbol{b}$. $\because \overrightarrow{C F} / / \overrightarrow{C E}, \therefore \frac{\frac{\lambda}{1+\lambda}}{\frac{1}{10}}=\frac{1}{\frac{9}{10}}, \therefore \lambda=\frac{1}{8}$.

17693

["8945.jpg"]

C

null

高二

设 $0 \leq \theta<2 \pi$, 已知两个向量 $\overrightarrow{O P}_{1}=(\cos \theta, \sin \theta)$, $\overrightarrow{O P_{2}}=(2+\sin \theta, 2-\cos \theta)$, 则向量 $\overrightarrow{P_{1} P_{2}}$ 长度的最大值是 ( )

A. $\sqrt{2}$ B. $\sqrt{3}$ C. $3 \sqrt{2}$ D. $2 \sqrt{3}$

度量几何学

<ImageHere> $\therefore\left|\overrightarrow{P_{1} P_{2}}\right|=\sqrt{(2+\sin \theta-\cos \theta)^{2}+(2-\cos \theta-\sin \theta)^{2}}=\sqrt{10-8 \cos \theta} \leq 3 \sqrt{2}$. 当 $\cos \theta=-1$ 时, $\left|\overrightarrow{P_{1} P_{2}}\right|$ 有最大值 $3 \sqrt{2}$, 故选 C.

17708

[]

A

null

高二

已知向量 $\boldsymbol{a}, \boldsymbol{b}$ 满足 $|\boldsymbol{a}|=\sqrt{6},|\boldsymbol{b}|=\sqrt{2},(\boldsymbol{a}-\boldsymbol{b}) \cdot \boldsymbol{b}=1$, 则向量 $\boldsymbol{a}, \boldsymbol{b}$ 夹角的大小等于 ( ) $\begin{array}{llll}\text {

A. } 30^{\circ} & \text { B. } 45^{\circ} & \text { C. } 60^{\circ} & \text { D. } 120^{\circ}\end{array}$

度量几何学

由 $(\boldsymbol{a}-\boldsymbol{b}) \cdot \boldsymbol{b}=1$ ，可得 $\boldsymbol{a} \cdot \boldsymbol{b}-\boldsymbol{b}^{2}=1$ ，所以， 所以 $\cos \langle\boldsymbol{a}, \boldsymbol{b}\rangle=\frac{\boldsymbol{a} \cdot \boldsymbol{b}}{|\boldsymbol{a}| \cdot|\boldsymbol{b}|}=\frac{3}{\sqrt{6} \cdot \sqrt{2}}=\frac{\sqrt{3}}{2}$, 而 $\left.0^{\circ} \leq<\boldsymbol{a}, \boldsymbol{b}\right\rangle \leq 180^{\circ}$, 则向量 $\boldsymbol{a}, \boldsymbol{b}$ 夹角的大小为 $30^{\circ}$, 故选 A.

17712

[]

A

null

高二

已知 $A(1,2), B(2,5), \overrightarrow{B C}=(-2,-4)$, 则 $\cos \langle\overrightarrow{A B}, \overrightarrow{A C}\rangle=$ ( )

A. $-\frac{2 \sqrt{5}}{5}$ B. $-\frac{\sqrt{5}}{5}$ C. $\frac{\sqrt{5}}{5}$ D. $\frac{2 \sqrt{5}}{5}$

度量几何学

$\overrightarrow{A B}=(1,3), \overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{B C}=(1,3)+(-2,-4)=(-1,-1)$, 所以 $\cos \langle\overrightarrow{A B}, \overrightarrow{A C}\rangle=\frac{\overrightarrow{A B} \cdot \overrightarrow{A C}}{|\overrightarrow{A B}| \cdot|\overrightarrow{A C}|}=\frac{-4}{\sqrt{10} \times \sqrt{2}}=-\frac{2 \sqrt{5}}{5}$, 故选 A.

17717

[]

B

null

高二

已知单位向量 $\boldsymbol{a}, \boldsymbol{b}$ 满足 $|\boldsymbol{a}-\boldsymbol{b}|+2 \sqrt{3} \boldsymbol{a} \cdot \boldsymbol{b}=0$, 则 $|\boldsymbol{a}+\boldsymbol{b}|(t \in \mathrm{R})$ 的最小值为 ( )\n\n

A. $ \frac{\sqrt{2}}{3} B. \frac{\sqrt{3}}{2} C. \frac{2 \sqrt{2}}{3} D. \frac{\sqrt{2}}{2}$

度量几何学

由 $|\boldsymbol{a}-\boldsymbol{b}|+2 \sqrt{3} \boldsymbol{a} \cdot \boldsymbol{b}=0$ ，得 $|\boldsymbol{a}-\boldsymbol{b}|=-2 \sqrt{3} \boldsymbol{a} \cdot \boldsymbol{b}$,两边平方, 得 $\boldsymbol{a}^{2}-2 \boldsymbol{a} \cdot \boldsymbol{b}+\boldsymbol{b}^{2}=12(\boldsymbol{a} \cdot \boldsymbol{b})^{2}$, 即 $12(\boldsymbol{a} \cdot \boldsymbol{b})^{2}+2 \boldsymbol{a} \cdot \boldsymbol{b}-2=0$ ，整理得 $(2 \boldsymbol{a} \cdot \boldsymbol{b}+1)(3 \boldsymbol{a} \cdot \boldsymbol{b}-1)=0$ ，所以 $\boldsymbol{a} \cdot \boldsymbol{b}=-\frac{1}{2}$ 或 $\boldsymbol{a}\cdot \boldsymbol{b}=\frac{1}{3} ，$因为 $|\boldsymbol{a}-\boldsymbol{b}|=-2 \sqrt{3} \boldsymbol{a} \cdot \boldsymbol{b} \geq 0$, 所以 $\boldsymbol{a} \cdot \boldsymbol{b} \leq 0$ ，所以 $\boldsymbol{a} \cdot \boldsymbol{b}=-\frac{1}{2}$ ，所以 $|\boldsymbol{t a}+\boldsymbol{b}|=\sqrt{|\boldsymbol{t a}+\boldsymbol{b}|^{2}}=\sqrt{t^{2}+1+2 t \boldsymbol{a} \cdot \boldsymbol{b}}=\sqrt{t^{2}-t+1}=\sqrt{\left(t-\frac{1}{2}\right)^{2}+\frac{3}{4}} \geq \frac{\sqrt{3}}{2}$,故选 B.

18375

[]

D

null

高二

已知角 $\theta$ 的终边过点 $(4,-3)$, 则 $\cos (\pi-\theta)=(\quad)$

A. $\frac{3}{5}$ B. $-\frac{3}{5}$ C. $\frac{4}{5}$ D. $-\frac{4}{5}$

度量几何学

解: $\because$ 角 $\theta$ 的终边过点 $(4,-3), \therefore \cos \theta=\frac{4}{5}, \therefore \cos (\pi-\theta)=-\cos \theta=-\frac{4}{5}$, 故选: D.

18395

[]

C

null

高二

下列三角函数值的符号判断错误的是( )

A.$\sin 165^{\circ}>0$ B. $\cos 280^{\circ}>0$ C. $\tan 170^{\circ}>0$ D. ${\tan 310^{\circ}<0}$

度量几何学

$165^{\circ}$ 是第二象限角, 因此 $\sin 165^{\circ}>0$ 正确; $280^{\circ}$ 是第四象限角, 因此 $\cos 280^{\circ}>0$ 正确; $170^{\circ}$是第二象限角, 因此 $\tan 170^{\circ}<0$, 故 C 错误; $310^{\circ}$ 是第四象限角, 因此 $\tan 310^{\circ}<0$​ 正确.故选C.

18396

["9101.jpg", "9102.jpg"]

A

null

高二

已知圆 $O$ 与直线 $l$ 相切于 $A$, 点 $P, Q$ 同时从点 $A$ 出发, $P$ 沿着直线 $l$ 向右、 $Q$ 沿着圆周按逆时针以相同的速度运动, 当 $Q$ 运动到点 $A$ 时, 点 $P$ 也停止运动, 连接 $O Q, O P$ （如图）, 则阴影部分面积 $S_{1}, S_{2}$ 的大小关系是 ( )<ImageHere>

A. $S_{1}=S_{2}$ B. $S_{1} \leq S_{2}$ C. $S_{1} \geq S_{2}$ D. 先 $S_{1}<S_{2}$, 再 $S_{1}=S_{2}$, 最后 $S_{1}>S_{2}$

度量几何学

如图所示, 因为直线 $l$ 与圆 $O$ 相切, 所以 $O A \perp A P$, 所以扇形的面积为 $S_{\text {扇形 } A O Q}=\frac{1}{2} \cdot A Q \cdot r=\frac{1}{2} \cdot A Q \cdot O A, S_{\triangle A O P}=\frac{1}{2} \cdot O A \cdot A P$, 因为 $A Q=A P$, 所以扇形 $A O Q$ 的面积 $S_{\text {扇形 } A O Q}=S_{\triangle A O P}$, 即 $S_{\text {扇形AOQ }}-S_{\text {扇形AOB }}=S_{\triangle A O P}-S_{\text {扇形 } A O B}$, 所以 $S_{1}=S_{2}$,故选A. <ImageHere>

18398

["9103.jpg"]

C

null

高二

已知弧度数为 2 的圆心角所对的弦长为 2 , 则这个圆心角所对的弧长是 ( )

A. 2 B. $\frac{1}{\sin 1}$ c. $\frac{2}{\sin 1}$ D. $\sin 2$

度量几何学

如图所示, <ImageHere>设扇形 $A O B$ 中, 圆心角 $\theta=\angle A O B=2$, 弦长 $A B=2$,过 $O$ 点作 $O C \perp A B$ 于点 $C$, 延长 $O C$, 交弧 $A B$ 于 $D$ 点, 则 $\angle A O D=\angle B O D=1, A C=\frac{1}{2} A B=1$. $\because$ 在 Rt $\triangle A C O$ 中, $A O=\frac{A C}{\sin \angle A O C}=\frac{1}{\sin 1}$, $\therefore$ 扇形 $A O B$ 的半径 $r=\frac{1}{\sin 1}$, $\therefore$ 弧 $A B$ 的长 $l=2 \times \frac{1}{\sin 1}=\frac{2}{\sin 1}$. 故选 C.

18399

["9104.jpg"]

C

null

高二

集合 $\left\{\alpha \mid k \cdot 180^{\circ}+45^{\circ} \leq \alpha \leq k \cdot 180^{\circ}+90^{\circ}, k \in Z\right\}$ 中的角所表示的范围（阴影部分）是（）

A.<ImageHere>B.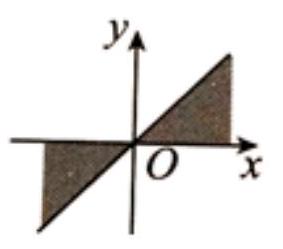C.D.

度量几何学

当 $k=0$ 时, $k \cdot 180^{\circ}+45^{\circ} \leq \alpha \leq k \cdot 180^{\circ}+90^{\circ}$ 即 $45^{\circ} \leq \alpha \leq 90^{\circ}$, 即选项 $C$ 中第一象限所示的部分; 当 $k=1$ 时, $k \cdot 180^{\circ}+45^{\circ} \leq \alpha \leq k \cdot 180^{\circ}+90^{\circ}$ 即 $225^{\circ} \leq \alpha \leq 270^{\circ}$, 即选项 $C$ 中第三象限所示的部分;当 $k=2$ 时，其所表示的角的范围与 $k=0$ 表示的范围一致. 综上可得, 选项 $C$ 表示集合 $\left\{\alpha \mid k \cdot 180^{\circ}+45^{\circ} \leq \alpha \leq k \cdot 180^{\circ}+90^{\circ}, k \in Z\right\}$ 中的角所表示的范围.故选: C.

18952

["9177.jpg"]

D

null

高二

设函数 $f(x)=\sin \left(2 x+\frac{\pi}{4}\right)\left(x \in\left[0, \frac{9 \pi}{8}\right]\right)$, 若方程 $f(x)=a$ 恰好有三个根, 分别为 $x_{1}, x_{2}, x_{3}\left(x_{1}<x_{2}<x_{3}\right)$, 则 $2 x_{1}+3 x_{2}+x_{3}$ 的值为 ( )

A. $\pi$ B. $\frac{3 \pi}{4}$ C. $\frac{3 \pi}{2}$ D. $\frac{7 \pi}{4}$

度量几何学

作出函数 $y=f(x)$ 的图象如图, 由图可知直线 $y=a$ 与 $y=f(x)$ 的图象的交点 $A, B$ 关于直线 $x=\frac{\pi}{8}$ 对称, 交点 $B, C$ 关于直线 $x=\frac{5 \pi}{8}$ 对称,所以 $x_{1}+x_{2}=\frac{\pi}{4}, x_{2}+x_{3}=\frac{5 \pi}{4}$, 所以 $2 x_{1}+3 x_{2}+x_{3}=2\left(x_{1}+x_{2}\right)+\left(x_{2}+x_{3}\right)$ <ImageHere> $=\frac{2 \pi}{4}+\frac{5 \pi}{4}=\frac{7 \pi}{4}$. 故选 D

18964

[]

D

null

高二

在 $\triangle A B C$ 中, $a, b, c$ 分别为角 $A$, $B, C$ 的对边, 若 $\triangle A B C$ 的面积为 $S$, 且 $4 \sqrt{3} S=(a+b)^{2}-c^{2}$, 则 $\sin \left(C+\frac{\pi}{4}\right)=$

A. 1 B. $\frac{\sqrt{2}}{2}$ C. $\frac{\sqrt{6}-\sqrt{2}}{4}$ D. $\frac{\sqrt{6}+\sqrt{2}}{4}$

度量几何学

由 $4 \sqrt{3} S=(a+b)^{2}-c^{2}$, 得 $4 \sqrt{3} \times \frac{1}{2} a b \sin C=a^{2}+b^{2}-c^{2}+2 a b$, $\because a^{2}+b^{2}-c^{2}=2 a b \cos C, \therefore 2 \sqrt{3} a b \sin C=2 a b \cos C+2 a b$, 即 $\sqrt{3} \sin C-\cos C=1$, 即 $2 \sin \left(C-\frac{\pi}{6}\right)=1$, 则 $\sin \left(C-\frac{\pi}{6}\right)=\frac{1}{2}$, $\because 0<C<\pi, \therefore-\frac{\pi}{6}<C-\frac{\pi}{6}<\frac{5 \pi}{6}, \therefore C-\frac{\pi}{6}=\frac{\pi}{6}$, 即 $C=\frac{\pi}{3}$, 则 $\sin \left(C+\frac{\pi}{4}\right)=\sin \left(\frac{\pi}{3}+\frac{\pi}{4}\right)=\sin \frac{\pi}{3} \cos \frac{\pi}{4}+\cos \frac{\pi}{3} \sin \frac{\pi}{4}=\frac{\sqrt{3}}{2} \times \frac{\sqrt{2}}{2}+\frac{1}{2} \times \frac{\sqrt{2}}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$, 故选 D.

17503

[]

A

null

高二

已知 $\sin \left(\frac{\pi}{6}+\alpha\right)=\frac{3}{5}, \frac{\pi}{3}<\alpha<\frac{5 \pi}{6}$, 则 $\cos \alpha$ 的值是( A )

A. $\frac{3-4 \sqrt{3}}{10}$ B. $\frac{4-3 \sqrt{3}}{10}$ C. $\frac{2 \sqrt{3}-3}{5}$ D. $\frac{3-2 \sqrt{3}}{5}$

度量几何学

[解析] $\because \frac{\pi}{3}<\alpha<\frac{5 \pi}{6}, \therefore \frac{\pi}{2}<\frac{\pi}{6}+\alpha<\pi$. $\therefore \cos \left(\frac{\pi}{6}+\alpha\right)=-\sqrt{1-\sin ^{2}\left(\frac{\pi}{6}+\alpha\right)}=-\frac{4}{5}$. $\therefore \cos \alpha=\cos \left[\left(\frac{\pi}{6}+\alpha\right)-\frac{\pi}{6}\right]$ $=\cos \left(\frac{\pi}{6}+\alpha\right) \cos \frac{\pi}{6}+\sin \left(\frac{\pi}{6}+\alpha\right) \sin \frac{\pi}{6}$ $=-\frac{4}{5} \times \frac{\sqrt{3}}{2}+\frac{3}{5} \times \frac{1}{2}=\frac{3-4 \sqrt{3}}{10}$.

17509

[]

C

null

高二

若 $\cos (\alpha-\beta)=\frac{\sqrt{5}}{5}, \cos 2 \alpha=\frac{\sqrt{10}}{10}$, 且 $\alpha 、 \beta$ 均为锐角, $\alpha<\beta$, 则 $\alpha+\beta$ 的值为 ( C )

A. $\frac{\pi}{6}$ B. $\frac{\pi}{4}$ C. $\frac{3 \pi}{4}$ D. $\frac{5 \pi}{6}$

度量几何学

析] $\because 0<\alpha<\frac{\pi}{2}, 0<\beta<\frac{\pi}{2}, \quad \alpha<\beta$, $\therefore-\frac{\pi}{2}<\alpha-\beta<0$. 又 $\cos (\alpha-\beta)=\frac{\sqrt{5}}{5}$, $\therefore \sin (\alpha-\beta)=-\sqrt{1-\cos ^{2}(\alpha-\beta)}=-\frac{2 \sqrt{5}}{5}$. 又 $\because 0<2 \alpha<\pi, \cos 2 \alpha=\frac{\sqrt{10}}{10}$, $\therefore \sin 2 \alpha=\sqrt{1-\cos ^{2} 2 \alpha}=\frac{3 \sqrt{10}}{10}$. $\therefore \cos (\alpha+\beta)=\cos [2 \alpha-(\alpha-\beta)]=\cos 2 \alpha \cos (\alpha-\beta)+\sin 2 \alpha \sin (\alpha-\beta)=\frac{\sqrt{10}}{10} \times \frac{\sqrt{5}}{5}+\frac{3 \sqrt{10}}{10} \times\left(-\frac{2 \sqrt{5}}{5}\right)=-\frac{\sqrt{2}}{2}$. 又 $0<\alpha+\beta<\pi$, 故 $\alpha+\beta=\frac{3 \pi}{4}$.

17299

[]

D

null

高二

若角 $\alpha$ 的终边经过点 $M(0,-3)$, 则角 $\alpha(\quad)$

A.是第三象限角 B $\cdot$ 是第四象限角 $\mathrm{C}$ $\cdot$ 既是第三象限角又是第四象限角 $\mathrm{D}$ $\cdot$ 不属于任何一个象限

度量几何学

解析: $\because$ 点 $M(0,-3)$ 在 $y$ 轴负半轴上, $\therefore$ 角 $\alpha$ 不属于任何一个象限. 答案: D

17301

[]

D

null

高二

11.若角 $\alpha$ 与 $65^{\circ}$ 角的终边相同, 角 $\beta$ 与 $-115^{\circ}$ 角的终边相同, 那么 $\alpha$ 与 $\beta$ 之间的关系是 $(\quad)$

$\mathrm{A} \cdot \alpha+\beta=-50^{\circ}$ $\mathrm{B} \cdot \alpha-\beta=180^{\circ}$ $\mathrm{C} \cdot \alpha+\beta=k \cdot 360^{\circ}+180^{\circ}(k \in \mathbf{Z})$ $\mathrm{D} \cdot \alpha-\beta=k \cdot 360^{\circ}+180^{\circ}(k \in \mathbf{Z})$

度量几何学

由题意可知, $\alpha=k_{1} \cdot 360^{\circ}+65^{\circ}\left(k_{1} \in \mathbf{Z}\right), \beta=k_{2} \cdot 360^{\circ}-115^{\circ}\left(k_{2} \in \mathbf{Z}\right)$, 所以 $\alpha-\beta=\left(k_{1}-k_{2}\right) \cdot 360^{\circ}+180^{\circ}$,记 $k=k_{1}-k_{2} \in \mathbf{Z}$, 故 $\alpha-\beta=k \cdot 360^{\circ}+180^{\circ}(k \in \mathbf{Z})$.

17305

[]

D

null

高二

把一条射线绕着端点按顺时针方向旋转 $240^{\circ}$ 所形成的角是 ( )

A. 120^{\circ} B. $-120^{\circ}$ C $\cdot 240^{\circ}$ D. $-240^{\circ}$

度量几何学

解析: 一条射线绕着端点按顺时针方向旋转 $240^{\circ}$ 所形成的角是 $-240^{\circ}$, 故选 D. 答案: D

17306

[]

C

null

高二

若角的顶点在原点, 角的始边与 $x$ 轴的非负半轴重合, 给出下列四个命题: (1) $0^{\circ}$ 角是第一象限角; (2)相等的角的终边一定相同; (3)终边相同的角有无限多个; (4)与 $-30^{\circ}$ 角终边相同的角都是第四象限角. 其中正确的有( )

A.$ 1$ 个 B. 2 个 $\mathrm{C} \cdot 3$ 个 D. 4 个

度量几何学

解析: $0^{\circ}$ 角是轴线角而不是象限角, (1)不正确; (2)显然正确; 终边相同的角有无限多个, 并且相差 $360^{\circ}$的整数倍, 所以(3)正确; $-30^{\circ}$ 角是第四象限角, 故(4)正确. 答案: C

17307

[]

C

null

高二

若 $\alpha$ 为锐角, 则下列各角中一定为第四象限角的是( )

A. $90^{\circ}-\alpha$ B. $90^{\circ}+\alpha$ $\mathrm{C} \cdot 360^{\circ}-\alpha$ D. $180^{\circ}+\alpha$

度量几何学

解析: $\because 0^{\circ}<\alpha<90^{\circ}, \therefore 270^{\circ}<360^{\circ}-\alpha<360^{\circ}$, 故选 C. 答案: C

17308

[]

D

null

高二

若角 $\alpha$ 与角 $\beta$ 的终边关于 $y$ 轴对称, 则必有 ( )

A.$ \alpha+\beta=90^{\circ}$ B $\cdot \alpha+\beta=k \cdot 360^{\circ}+90^{\circ}(k \in \mathbf{Z})$ C $\cdot \alpha+\beta=k \cdot 360^{\circ}(k \in \mathbf{Z})$ $\mathrm{D} \cdot \alpha+\beta=(2 k+1) 180^{\circ}(k \in \mathbf{Z})$

度量几何学

解析: $\alpha$ 与 $\beta$ 的终边关于 $y$ 轴对称, 则 $\alpha$ 与 $180^{\circ}-\beta$ 终边相同, 故 $\alpha=180^{\circ}-\beta+360^{\circ} \cdot k$, 即 $\alpha+\beta=(2 k$ $+1) \cdot 180^{\circ}, k \in \mathbf{Z}$. 答案: D

17313

[]

D

null

高二

$-\frac{25 \pi}{6}$ 的角是 ( )

A. 第一象限的角 B. 第二象限的角 C. 第三象限的角 D. 第四象限的角

度量几何学

因为 $-\frac{25 \pi}{6}=-\frac{\pi}{6}-4 \pi$,所以 $-\frac{25 \pi}{6}$ 与 $-\frac{\pi}{6}$ 的终边相同, 为第四象限的角. 【答案】D

17315

[]

B

null

高二

时钟的分针在 1 点到 3 点 20 分这段时间里转过的弧度数为( )

A. $\frac{14}{3} \pi$ B. $-\frac{14}{3} \pi$ C. $\frac{7}{18} \pi$ D. $-\frac{7}{18} \pi$

度量几何学

分针在 1 点到 3 点 20 分这段时间里, 顺时针转过了两周又一周的 $\frac{1}{3}$, 用弧度制表示就是: $-4 \pi-\frac{1}{3} \times 2 \pi=-\frac{14}{3} \pi$. ## 【答案】 B

17316

[]

B

null

高二

圆的半径是 $6 \mathrm{~cm}$, 则 $15^{\circ}$ 的圆心角与圆弧围成的扇形面积是( )

A. $\frac{\pi}{2} \mathrm{~cm}^{2}$ B. $\frac{3 \pi}{2} \mathrm{~cm}^{2}$ C. $\pi \mathrm{cm}^{2}$ D. $3 \pi \mathrm{cm}^{2}$

度量几何学

$15^{\circ}=\frac{\pi}{12}$, 则 $S=\frac{1}{2}|\alpha| r^{2}=\frac{1}{2} \times \frac{\pi}{12} \times 6^{2}=\frac{3 \pi}{2}\left(\mathrm{~cm}^{2}\right)$. 【答案】 B

17317

[]

D

null

高二

下列说法不正确的是 ( )

A. “度” 与 “弧度” 是度量角的两种不同的度量单位 B. $1^{\circ}$ 的角是周角的 $\frac{1}{360}, 1$ 弧度的角是周角的 $\frac{1}{2 \pi}$ C. $1 \mathrm{rad}$ 的角比 $1^{\circ}$ 的角要大 D. 用角度制和弧度制度量角, 都与圆的半径有关

度量几何学

用角度制和弧度制度量角，都与圆的半径无关。 ## 【答案】D

17318

["8884.jpg", "8885.jpg", "8886.jpg", "8887.jpg"]

C

null

高二

集合 $\left\{\alpha \left\lvert\, k \pi+\frac{\pi}{4} \leqslant \alpha \leqslant k \pi+\frac{\pi}{2}\right., k \in \mathbf{Z}\right\}$ 中角所表示的范围(阴影部分)是( )

A.<ImageHere> B.<ImageHere> C.<ImageHere> D.<ImageHere>

度量几何学

$k$ 为偶数时，集合对应的区域为第一象限内直线 $y=x$ 左上部分(包含边界), $k$ 为奇数时，集合对应的区域为第三象限内直线 $y=x$ 的右下部分(包含边界)。故选 C.

17323

[]

D

null

高二

$1920^{\circ}$ 的角化为弧度数为 $(\quad)$

A. $\frac{16}{3}$ B. $\frac{32}{3}$ C. $\frac{16}{3} \pi$ D. $\frac{32}{3} \pi$

度量几何学

解析: $\because 1^{\circ}=\frac{\pi}{180} \mathrm{rad}$, $\therefore 1920^{\circ}=1920 \times \frac{\pi}{180} \mathrm{rad}=\frac{32}{3} \pi \mathrm{rad}$. 答案: D

17329

[]

C

null

高二

角 $\alpha$ 的终边落在区间 $\left(-3 \pi,-\frac{5 \pi}{2}\right)$ 内, 则角 $\alpha$ 所在的象限是 $(\quad)$

A.第一象限 B. 第二象限 $\mathrm{C}$ $\cdot$第三象限 D. 第四象限

度量几何学

解析: $-3 \pi$ 的终边在 $x$ 轴的非正半轴上, $-\frac{5}{2} \pi$ 的终边在 $y$ 轴的非正半轴上, 故角 $\alpha$ 为第三象限角. 答案: C

17330

[]

C

null

高二

下列与 $\frac{9 \pi}{4}$ 的终边相同的角的表达式中, 正确的是( )

A.$ 2 k \pi+45^{\circ}(k \in \mathbf{Z})$ B $\cdot k \cdot 360^{\circ}+\frac{9 \pi}{4}(k \in \mathbf{Z})$ $\mathrm{C} \cdot k \cdot 360^{\circ}-315^{\circ}(k \in \mathbf{Z})$ D $\cdot k \pi+\frac{5 \pi}{4}(k \in \mathbf{Z})$

度量几何学

解析: A, B 中弧度与角度混用, 不正确. $\frac{9}{4} \pi=2 \pi+\frac{\pi}{4}$, 所以 $\frac{9}{4} \pi$ 与 $\frac{\pi}{4}$ 终边相同. $-315^{\circ}=-360^{\circ}+45^{\circ}$, 所以 $-315^{\circ}$ 也与 $45^{\circ}$ 终边相同. 故选 C. 答案: C

17331

["8889.jpg"]

C

null

高二

$圆弧长度等于其所在圆内接正三角形的边长, 则该圆弧所对圆心角的弧度数为 $(\quad)

A. $\frac{\pi}{3} \quad$ B. $\frac{2 \pi}{3}$ C. $\sqrt{3}$ D. 2

度量几何学

解析: 如右图<ImageHere>, 设圆的半径为 $R$, 则圆的内接正三角形的边长为 $\sqrt{3} R$, 所以圆弧长度为 $\sqrt{3} R$ 的圆心角的弧度数 $\alpha=\frac{\sqrt{3} R}{R}=\sqrt{3}$. 答案: C

17523

[]

B

null

高二

若 $\sin \left(\frac{\pi}{6}-\alpha\right)=\frac{1}{3}$, 则 $\cos \left(\frac{2 \pi}{3}+2 \alpha\right)=(\quad)$

A. $-\frac{1}{3}$ B. $-\frac{7}{9}$ C. $\frac{7}{9}$ D. $\frac{1}{3}$

度量几何学

析] $\cos \left(\frac{2 \pi}{3}+2 \alpha\right)=2 \cos ^{2}\left(\frac{\pi}{3}+\alpha\right)-1=2 \cos ^{2}\left[\frac{\pi}{2}-\left(\frac{\pi}{6}-\alpha\right)\right]-1=2 \sin ^{2}\left(\frac{\pi}{6}-\alpha\right)-1=\frac{2}{9}-1=-\frac{7}{9}$.

17373

[]

C

null

高二

若 $\tan \alpha=3$, 则 $2 \sin \alpha \cos \alpha=(\quad)$

A. $\\pm \\frac{3}{5}$ B. $-\\frac{3}{5}$ C. $\\frac{3}{5}$ D. $\\frac{4}{5}$

度量几何学

$2 \sin \alpha \cos \alpha=\frac{2 \sin \alpha \cos \alpha}{\sin ^{2} \alpha+\cos ^{2} \alpha}=\frac{2 \tan \alpha}{\tan ^{2} \alpha+1}=\frac{6}{10}=\frac{3}{5}$.

17375

[]

B

null

高二

若 $\alpha \in[0,2 \pi)$, 且有 $\sqrt{1-\cos ^{2} \alpha}+\sqrt{1-\sin ^{2} \alpha}=\sin \alpha-\cos \alpha$, 则角 $\alpha$ 的取值范围为 ( )

A. $\left[0, \frac{\pi}{2}\right)$ B. $\left[\frac{\pi}{2}, \pi\right]$ C. $\left(\frac{\pi}{2}, \pi\right)$ D. $\left[\pi, \frac{3}{2} \pi\right]$

度量几何学

因为 $\sqrt{1-\cos ^{2} \alpha}+\sqrt{1-\sin ^{2} \alpha}=\sin \alpha-\cos \alpha$, 所以 $\left\{\begin{array}{l}\sin \alpha \geqslant 0, \\ \cos \alpha \leqslant 0,\end{array}\right.$ 又 $\alpha \in[0,2 \pi)$,所以 $\alpha \in\left[\frac{\pi}{2}, \pi\right]$, 故选 B. ## 【答案】 B

17566

[]

B

null

高二

若 $\alpha 、 \beta$ 均为锐角, $\sin \alpha=\frac{2 \sqrt{5}}{5}, \sin (\alpha+\beta)=\frac{3}{5}$, 则 $\cos \beta$ 等于导学号 14434996 ( B )

A. $\frac{2 \sqrt{5}}{5}$ B. $\frac{2 \sqrt{5}}{25}$ C. $\frac{2 \sqrt{5}}{5}$ 或 $\frac{2 \sqrt{5}}{25}$ D. $-\frac{2 \sqrt{5}}{25}$

度量几何学

[解析] $\because \alpha$ 与 $\beta$ 均为锐角, 且 $\sin \alpha=\frac{2 \sqrt{5}}{5}>\sin (\alpha+\beta)=\frac{3}{5}, \therefore \alpha+\beta$ 为钝角, 又由 $\sin (\alpha+\beta)=\frac{3}{5}$ 得, $\cos (\alpha+\beta)=-\frac{4}{5}$, 由 $\sin \alpha=\frac{2 \sqrt{5}}{5}$ 得, $\cos \alpha=\frac{\sqrt{5}}{5}$, $\therefore \cos \beta=\cos [(\alpha+\beta)-\alpha]=\cos (\alpha+\beta) \cos \alpha+\sin (\alpha+\beta) \sin \alpha=-\frac{4}{5} \times \frac{\sqrt{5}}{5}+\frac{3}{5} \times \frac{2 \sqrt{5}}{5}=\frac{2 \sqrt{5}}{25}$, 故选 B.

17395

[]

D

null

高二

已知角 $\alpha$ 终边上异于原点的一点 $P$ 且 $|P O|=r$, 则点 $P$ 的坐标为 $(\quad)$

A. $P(\sin \alpha, \cos \alpha)$ B. $P(\cos \alpha, \sin \alpha)$ C. $P(r \sin \alpha, r \cos \alpha)$ D. $P(r \cos \alpha, r \sin \alpha)$

度量几何学

设 $P(x, y)$, 则 $\sin \alpha=\frac{y}{r}, \therefore y=r \sin \alpha$, 又 $\cos \alpha=\frac{x}{r}, x=r \cos \alpha, \therefore P(r \cos \alpha, r \sin \alpha)$, 故选 D. 【答案】 $\mathrm{D}$

17403

["8897.jpg"]

C

null

高二

在 $[0,2 \pi]$ 内, 不等式 $\sin x<-\frac{\sqrt{3}}{2}$ 的解集是( )

A. $(0, \pi)$ B. $\left(\frac{\pi}{3}, \frac{4 \pi}{3}\right)$ C. $\left(\frac{4 \pi}{3}, \frac{5 \pi}{3}\right)$ D. $\left(\frac{5 \pi}{3}, 2 \pi\right)$

度量几何学

画出 $y=\sin x, x \in[0,2 \pi]$ 的草图如下:<ImageHere> 因为 $\sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}$, 所以 $\sin \left(\pi+\frac{\pi}{3}\right)=-\frac{\sqrt{3}}{2}$, $\sin \left(2 \pi-\frac{\pi}{3}\right)=-\frac{\sqrt{3}}{2}$. 即在 $[0,2 \pi]$ 内, 满足 $\sin x=-\frac{\sqrt{3}}{2}$ 的是 $x=\frac{4 \pi}{3}$ 或 $x=\frac{5 \pi}{3}$. 可知不等式 $\sin x<-\frac{\sqrt{3}}{2}$ 的解集是 $\left(\frac{4 \pi}{3}, \frac{5 \pi}{3}\right)$. ## 【答案】C

17449

[]

B

null

高二

10.关于函数 $f(x)=4 \sin \left(2 x+\frac{\pi}{3}\right)$ $(x \in \mathbf{R})$, 有下列命题: (1)函数 $y=f(x)$ 的表达式可改写为 $y=4 \cos \left(2 x-\frac{\pi}{6}\right)$; (2)函数 $y=f(x)$ 是以 $2 \pi$ 为最小正周期的周期函数; (3)函数 $y=f(x)$ 的图象关于点 $\left(-\frac{\pi}{6}, 0\right)$ 对称; (4)函数 $y=f(x)$ 的图象关于直线 $x=-\frac{\pi}{6}$ 对称. 其中正确的是( )

A. (2)(3) B. (1)(3) C. (1)(4) D. (2)(4)

度量几何学

$f(x)=4 \sin \left(2 x+\frac{\pi}{3}\right)=4 \cos \left[\frac{\pi}{2}-\left(2 x+\frac{\pi}{3}\right)\right]$ $=4 \cos \left(\frac{\pi}{6}-2 x\right)=4 \cos \left(2 x-\frac{\pi}{6}\right)$, 故(1)正确; 函数 $f(x)$ 的最小正周期为 $\pi$, 故(2)错误; 由 $f\left(-\frac{\pi}{6}\right)=4 \sin \left[2 \times\left(-\frac{\pi}{6}\right)+\frac{\pi}{3}\right]=0$, 知函数 $y=f(x)$ 的图象关于点 $\left(-\frac{\pi}{6}, 0\right)$ 对称, 不关于直线 $x=-\frac{\pi}{6}$ 对称， 故(3)正确, (4)错误。 ## 【答案】 B

17452

[]

C

null

高二

下列关系式中正确的是( )

A. $\sin 11^{\circ}<\cos 10^{\circ}<\sin 168^{\circ}$ B. $\sin 168^{\circ}<\sin 11^{\circ}<\cos 10^{\circ}$ C. $\sin 11^{\circ}<\sin 168^{\circ}<\cos 10^{\circ}$ D. $\sin 168^{\circ}<\cos 10^{\circ}<\sin 11^{\circ}$

度量几何学

由诱导公式, 得 $\cos 10^{\circ}=\sin 80^{\circ}, \sin 168^{\circ}=\sin \left(180^{\circ}-12^{\circ}\right)=\sin 12^{\circ}$, 由正弦函数 $y=\sin x$在 $\left[0^{\circ}, 90^{\circ}\right]$ 上是单调递增的, 所以 $\sin 11^{\circ}<\sin 12^{\circ}<\sin 80^{\circ}$, 即 $\sin 11^{\circ}<\sin 168^{\circ}<\cos 10^{\circ}$. 故选 C. 【答案】 C

17588

["8922.jpg"]

B

null

高二

如图 1-6-9 所示, 有一广告气球, 直径为 $6 \mathrm{~m}$, 放在公司大楼上空, 当行人仰望气球中心的仰角 $\angle B A C$ $=30^{\circ}$ 时, 测得气球的视角为 $2^{\circ}$ (若 $\beta$ 很小时, 可取 $\left.\sin \beta \approx \beta\right)$, 试估算该气球的高 $B C$ 的值约为 (<ImageHere>图 1-6-9

A. $70 \mathrm{~m}$B. $86 \mathrm{~m}$C. $102 \mathrm{~m}$D. $118 \mathrm{~m}$

度量几何学

假设气球到人的距离 $A C$ 为 $s$,$\therefore 6=s \times \sin 2^{\circ}=s \times 2 \times \frac{2 \pi}{360}$,$\therefore s \approx 171.887 \mathrm{~m}$,$\therefore h=B C=s \times \sin 30^{\circ}=85.94 \mathrm{~m} \approx 86 \mathrm{~m}$.

17482

[]

A

null

高二

已知 $\cos \left(60^{\circ}+\alpha\right)=\frac{1}{3}$, 且 $-180^{\circ}<\alpha<-90^{\circ}$,则 $\cos \left(30^{\circ}-\alpha\right)$ 的值为 $(\quad)$\n

A. $-\frac{2 \sqrt{2}}{3}$ B. $\frac{2 \sqrt{2}}{3}$ C. $-\frac{\sqrt{2}}{3}$ D. $\frac{\sqrt{2}}{3}$

度量几何学

由 $-180^{\circ}<\alpha<-90^{\circ}$, 得 $-120^{\circ}<60^{\circ}+\alpha<-30^{\circ}$. 又 $\cos \left(60^{\circ}+\alpha\right)=\frac{1}{3}>0$, 所以 $-90^{\circ}<60^{\circ}+\alpha<-30^{\circ}$,即 $-150^{\circ}<\alpha<-90^{\circ}$, 所以 $120^{\circ}<30^{\circ}-\alpha<180^{\circ}, \cos \left(30^{\circ}-\alpha\right)<0$, 所以 $\cos \left(30^{\circ}-\alpha\right)=\sin \left(60^{\circ}+\alpha\right)=-$ $\sqrt{1-\cos ^{2}\left(60^{\circ}+\alpha\right)}=-\sqrt{1-\left(\frac{1}{3}\right)^{2}}=-\frac{2 \sqrt{2}}{3}$.\n\n答案: A\n\n

17483

[]

B

null

高二

如果 $\cos (\pi+A)=-\frac{1}{2}$, 那么 $\sin \left(\frac{\pi}{2}+A\right)$ 等于 $(\quad)$

A. $-\frac{1}{2}$ B. $\frac{1}{2}$ C. $-\frac{\sqrt{3}}{2} \quad$ D. $\frac{\sqrt{3}}{2}$

度量几何学

解析: $\cos (\pi+A)=-\cos A=-\frac{1}{2}$, $\therefore \cos A=\frac{1}{2}$, $\therefore \sin \left(\frac{\pi}{2}+A\right)=\cos A=\frac{1}{2}$. 答案: B

17486

[]

B

null

高二

若 $\sin (\pi+\alpha)+\cos \left(\frac{\pi}{2}+\alpha\right)=-m$, 则 $\cos \left(\frac{3 \pi}{2}-\alpha\right)+2 \sin (6 \pi-\alpha)$ 的值为 ( )

A. $-\frac{2}{3} m$ B. $-\frac{3}{2} m$ C. $\frac{2}{3} m$ D. $\frac{3}{2} m$

度量几何学

解析: $\because \sin (\pi+\alpha)+\cos \left(\frac{\pi}{2}+\alpha\right)=-m$, 即 $-\sin \alpha-\sin \alpha=-2 \sin \alpha=-m$ ，从而 $\sin \alpha=\frac{m}{2}$, $\therefore \cos \left(\frac{3 \pi}{2}-\alpha\right)+2 \sin (6 \pi-\alpha)=-\sin \alpha-2 \sin \alpha=-3 \sin \alpha=-\frac{3}{2} m$. 答案: B

18421

[]

B

null

高二

若 $\alpha, \beta$ 均为锐角, $\sin \alpha=\frac{2 \sqrt{5}}{5}, \sin (\alpha+\beta)=\frac{3}{5}$, 则 $\cos \beta=$

A. $\frac{2 \sqrt{5}}{5}$ B. $\frac{2 \sqrt{5}}{25}$ C. $\frac{2 \sqrt{5}}{5}$ 或 $\frac{2 \sqrt{5}}{25}$ D. $-\frac{2 \sqrt{5}}{25}$

度量几何学

$\because \alpha$ 为锐角, $\sin \alpha=\frac{2 \sqrt{5}}{5}>\frac{\sqrt{2}}{2} \mathrm{~s}, \therefore \alpha>45^{\circ}$ 且 $\cos \alpha=\frac{\sqrt{5}}{5}$, $\because \sin (\alpha+\beta)=\frac{3}{5}$, 且 $\frac{1}{2}<\frac{3}{5}<\frac{\sqrt{2}}{2}, \therefore \frac{\pi}{2}<\alpha+\beta<\pi$, $\therefore \cos (\alpha+\beta)=-\frac{4}{5}$, 则 $\cos \beta=\cos [(\alpha+\beta)-\alpha]=\cos (\alpha+\beta) \cos \alpha+\sin (\alpha+\beta)$ $\sin \alpha=-\frac{4}{5} \times \frac{\sqrt{5}}{5}+\frac{3}{5} \times \frac{2 \sqrt{5}}{5}=\frac{2 \sqrt{5}}{25}$. 故选 B.

20393

[]

D

null

高二

(2014$\cdot$福建) 设 $\mathrm{P}, \mathrm{Q}$ 分别为圆 $\mathrm{x}^{2}+(\mathrm{y}-6)^{2}=2$ 和粗圆 ${ }^{\frac{x^{2}}{10}}+\mathrm{y}^{2}=1$ 上的点, 则 $\mathrm{P}, \mathrm{Q}$ 两点间的最大距离是 ( )

A. $5 \sqrt{2}$ B. $\sqrt{4 \epsilon_{+}}+\sqrt{2}$ C. $7+\sqrt{2}$ D. $6 \quad \sqrt{2}$

度量几何学

答案:D 【解析】【解答】解：设椭圆上的点为 $(\mathrm{x}, \mathrm{y})$ ，则 $\because$ 圆 $x^{2}+(y-6)^{2}=2$ 的圆心为 $(0,6)$, 半径为 $\sqrt{2}$, $\therefore$ 椭圆上的点 $(x, y)$ 到圆心 $(0,6)$ 的距离为 $\sqrt{x^{2}+(y-6)^{2}}=\sqrt{10\left(1-y^{2}\right)+(y-6)^{2}}=$ $\sqrt{-9\left(y+\frac{2}{3}\right)^{2}+50} \leq 5 \sqrt{2}$, $\therefore \mathrm{P}, \mathrm{Q}$ 两点间的最大距离是 $5 \sqrt{2}+\mathrm{v}=6 \sqrt{2}$. 故选: D. 【分析】求出粗圆上的点与圆心的最大距离, 加上半径, 即可得出 $\mathrm{P}, \mathrm{Q}$ 两点间的最大距离.二、填空题

20397

["9348.jpg"]

D

null

高二

<ImageHere> $=90^{\circ}, riangle F_{1} P F_{2}$ 面积是 9, 则 $a+b=(\quad)$

A. 4 B. 5 C. 6 D. 7

度量几何学

答案：D 【解析】由双曲线焦点三角形面积公式得 $b^{2} \cot \frac{90^{\circ}}{2}=9 \therefore b^{2}=9 \therefore c^{2}-a^{2}=9$, $\because e=\frac{c}{a}=\frac{5}{4} \therefore c=5, a=4, a+b=7$ 12. 答案:D 【解析】 $2 b=8: \therefore b=4, A(-3,0), F(5,0)$, 因为 $F$ 到双曲线的渐近线距离为 $b$, 所以 $\odot F$ ： $(x-5)^{2}+y^{2}=16$, 设 $\mathrm{MN}$ 交 $x$ 轴于 $\mathrm{E}$, 则 $F E=\frac{4^{2}}{3+5}=2 \therefore A E=8-2=6, M E^{2}=A E \times E F=12 \therefore M N=2 M E=4 \sqrt{3}$ 故答案为: D. 分析 先由虚轴长为 8 得到 $\mathrm{b}$ 的值,由焦点 $\mathrm{F}$ 到双曲线的渐近线距离为 $\mathrm{b}$, 得到圆的方程, 由直线与圆相交的性质求出 FE 和 $\mathrm{AE}$ 的长, 再求 MN.

19500

[]

B

null

高二

若 $M=a^{2}+3 a b, \quad N=5 a b-b^{2}$, 则 $M, N$ 的大小关系是 ( )

A. $M>N$ B. $M \geq N$ C. $M<N$ D. $M \leq N$

算术

答案: B 解析: $\because M-N=a^{2}+3 a b-\left(5 a b-b^{2}\right)=a^{2}-2 a b+b^{2}=(a-b)^{2} \geq 0$, $\therefore M \geq N$, 故选 B.

19511

[]

A

null

高二

如果 $a<0, b>0$, 那么, 下列不等式中正确的是 ( )

A. $\frac{1}{a}<\frac{1}{b}$ B. $\sqrt{-a}<\sqrt{b}$ C. $a^{2}<b^{2}$ D. $|a|>|b|$

算术

答案: A

19513

[]

A

null

高二

不等式 $x(x-2)<0$ 的解集是 ( )

A. $(0,2)$ B. $(-\infty, 0) \cup(2,+\infty)$ C. $(-\infty, 0)$ D. $(2,+\infty)$

算术

不等式 $x(x-2)<0$ 对应方程的两个实数根是 0 和 $2, \therefore$ 不等式的解集是 $(0,2)$. 故选 A

19514

[]

B

null

高二

已知 $a, b>0$, 且 $a b=1$, 则 ( )

A. $a+b>2$ B. $a+b \geq 2$ C. $a+b<-2$ D. $a+b \leq-2$

算术

A. 因为 $a, b>0$, 且 $a b=1$, 则取 $a=b=1$ 可排除 A; $C D$ 取 $a=2, b=\frac{1}{2}$, 可排除 C、D; B. $a+b=a+\frac{1}{a} \geq 2$, 当且仅当 $a=b=1$ 时取等号.故选: B.

19521

[]

A

null

高二

已知数列 $\left\{a_{n}\right\}$ 的通项公式是 $a_{n}=\frac{2 n}{3 n-1}$, 那么这个数列是( )

A.递增数列 B.递减数列 C.摆动数列 D. 常数列

算术

解析: $\because a_{n+1}-a_{n}=\frac{2 n+2}{3 n+4}-\frac{2 n}{3 n-1}=\frac{2}{(3 n+4)(3 n-1)}>0$, $\therefore a_{n+1}>a_{n}$, 即数列为递增数列. 故选 A.

19531

[]

B

null

高二

数列 $\sqrt{2}, \sqrt{5}, 2 \sqrt{2}, \sqrt{11} \cdots$, 的一个通项公式是( )

A. $a_{n}=\sqrt{3 n-3}$ B. $a_{n}=\sqrt{3 n-1}$ C. $a_{n}=\sqrt{3 n+1}$ D. $a_{n}=\sqrt{3 n+3}$

算术

答案: B

19534

[]

B

null

高二

数列 $1,1,2,3, x, 8,13,21, \ldots$ 中的 $x$ 的值是 ( )

A. 4 B. 5 C. 6 D. 7

算术

答案: B 解析: 采用归纳猜想寻找规律, $1+1=2,1+2=3, \ldots, 8+13=21$, 所以 $2+3=x$, 所以 $x=5$. 故选 B

19535

[]

C

null

高二

数列 $\left\{a_{n}\right\}$ 中, $a_{1}=1$, 以后各项由公式 $a_{1} \cdot a_{2} \cdot a_{3} \cdot \ldots \cdot a_{n}=n^{2}$ 给出, 则 $a_{3}+a_{5}$ 等于 ( )

A. $\frac{25}{9}$ B. $\frac{25}{16}$ C. $\frac{61}{16}$ D. $\frac{31}{15}$

算术

答案: C 解析: $\because a_{1} \cdot a_{2} \cdot a_{3} \cdots a_{n}=n^{2}$ $\therefore a_{1} \cdot a_{2} \cdot a_{3}=32=9$, $a_{1} \cdot a_{2}=2^{2}=4$, $\therefore a_{3}=\frac{9}{4}$. $\therefore a_{1} \cdot a_{2} \cdot a_{3} a_{4}=4^{2}=16$, $a_{1} \cdot a_{2} \cdot a_{3} \cdot a_{4} \cdot a_{5}=5^{2}=25$, $\therefore a_{5}=\frac{25}{16}$, $\therefore a_{3}+a_{5}=\frac{9}{4}+\frac{25}{16}=\frac{61}{16}$. 故选 C.

19536

[]

B

null

高二

数列 $3,5,9,17,33, \cdots$ 的通项公式 $a_{n}$ 等于 ( )

A. $2^{n}$ B. $2^{n}+1$ C. $2^{n}-1$ D. $2^{n+1}$

算术

答案: B

19537

[]

C

null

高二

已知数列 $-3,7,-11,15 \ldots$, 则下列选项能表示数列的一个通项公式的是 ( )

A. $a_{n}=4 n-7$ B. $a_{n}=(-1)^{n}(4 n+1)$ C. $a_{n}=(-1)^{n} \cdot(4 n-1)$ D. $a_{n}=(-1)^{n+1} \cdot(4 n-1)$

算术

答案: C 解析: 设此数列为 $\left\{a_{n}\right\}$. 则第 $n$ 项的符号为 $(-1)^{n}$, 其绝对值为: $3,7,11,15, \ldots$, 为等差数列, $\left|a_{n}\right|=3+4(n-1)=4 n-1$. $\therefore a_{n}=(-1)^{n} \cdot(4 n-1)$. 故选: C.

18886

[]

D

null

高二

设 $\left\{a_{n}\right\}$ 是任意等差数列, 它的前 $n$ 项和、前 $2 n$ 项和与前 $4 n$ 项和分别为 $X 、 Y 、 Z$, 则下列等式中恒成立的是

A. $2 X+Z=3 Y$ B. $4 X+Z=4 Y$ C. $2 X+3 Z=7 Y$ D. $8 X+Z=6 Y$

算术

设等差数列的前 $3 n$ 项的和为 $R$, 则由等差数列的性质, 可得 $X, Y-X, R-Y, Z-R$成等差数列, 所以 $2(Y-X)=X+(R-Y)$, 解得 $R=3 Y-3 X$, 又因为 $2(R-Y)=$ $(Y-X)+(Z-R)$, 把 $R=3 Y-3 X$ 代入, 得 $8 X+Z=6 Y$, 故选 D.

18907

[]

D

null

高二

已知等差数列 $\left\{a_{n}\right\}$ 满足 $a_{1}=2$, 公差 $d \neq 0$, 且 $a_{1}, a_{2}, a_{5}$ 成等比数列, 则 $d=(\quad)$

A. 1 B. 2 C. 3 D. 4

算术

$a_{2}=2+d, a_{5}=2+4 d$, 因为 $a_{1}, a_{2}, a_{5}$ 成等比数列, 所以 $(2+d)^{2}=2(2+4 d)$, 解得 $d=4$ 。

18908

[]

A

null

高二

设等比数列 $\left\{a_{n}\right\}$ 的公比 $q=3$, 前 $n$ 和为 $S_{n}$, 则 $\frac{S_{4}}{a_{2}}$ 的值为 （）

A. $\frac{40}{3}$ B. $\frac{40}{9}$ C. $\frac{13}{3}$ D. 9

算术

$\frac{S_{4}}{a_{2}}=\frac{a_{1}\left(1-q^{4}\right)}{1-q} \div a_{1} q=\frac{1-3^{4}}{1-3} \div 3=\frac{40}{3}$, 故选 A.

18909

[]

A

null

高二

等差数列 $\left\{a_{n}\right\}$ 的公差为 $1, a_{1}, a_{2}, a_{5}$ 成等比数列, 则 $\left\{a_{n}\right\}$ 的前 10 项和为

A. 50 B. -50 C. 45 D. -45

算术

依题意, $a_{2}^{2}=a_{1} a_{5},\left(a_{1}+1\right)^{2}=a_{1}\left(a_{1}+4\right)$, 解得 $a_{1}=\frac{1}{2}$, 所以 $S_{10}=10 \times \frac{1}{2}$ $+\frac{10 \times 9}{2} \times 1=50$. 故选 A.

18910

[]

B

null

高二

已知等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}$, 若 $S_{5}=7, S_{10}=21$, 则 $S_{15}=(\quad)$

A. 35 B. 42 C. 49 D. 63

算术

设等差数列 $\left\{a_{n}\right\}$ 的公差为 $d$, 则 $S_{5}=5 a_{1}+10 d=7, S_{10}=10 a_{1}+45 d=21$,解得 $a_{1}=\frac{21}{25}, d=\frac{7}{25}$, 所以 $S_{15}=15 \times \frac{21}{25}+\frac{15 \times 14}{2} \times \frac{7}{25}=42$. 故选 B.

18918

[]

C

null

高二

《算法统宗》全称《新编直指算法统宗》, 是中国古代数学名著, 程大位著. 书中有如下问题: “今有五人均银四十两, 甲得十两四钱, 戊得五两六钱.问：次第均之，乙丙丁各该若干? ”意思是：有 5 人分 40 两银子, 甲分 10 两 4 钱, 戊分 5 两 6 钱, 且相邻两项差相等, 则乙丙丁各分几两几钱?（注: 1 两等于 10 钱）（）

乙分 8 两, 丙分 8 两, 丁分 8 两 B. 乙分 8 两 2 钱, 丙分 8 两, 丁分 7 两 8 钱 C. 乙分 9 两 2 钱, 丙分 8 两, 丁分 6 两 8 钱D. D. 乙分 9 两, 丙分 8 两, 丁分 7 两

算术

由题意可得甲、乙、丙、丁、戊所得钱数成等差数列 $\left\{a_{n}\right\}$, 则 $a_{1}=

18922

[]

D

null

高二

如果 $b<a<0$, 那么下列不等式成立的是（）

A. $\log _{2}|b|<\log _{2}|a|$ B. $\left(\frac{1}{2}\right)^{b}<\left(\frac{1}{2}\right)^{a}$ C. $b^{3}>a^{3}$ D. $a b<b^{2}$

算术

$\because b<a<0, \therefore \log _{2}|b|>\log _{2}|a|,\left(\frac{1}{2}\right)^{b}>\left(\frac{1}{2}\right)^{a}, \quad b^{3}<a^{3}, a b<b^{2}$, 故选 D。

18923

[]

D

null

高二

已知等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}$, 公差为 -2 , 且 $a_{7}$ 是 $a_{3}$与 $a_{9}$ 的等比中项, 则 $S_{10}$ 的值为 ( )

A. -110 B. -90 C. 90 D. 110

算术

$\because a_{7}$ 是 $a_{3}$ 与 $a_{9}$ 的等比中项, $\therefore a_{7}^{2}=a_{3} a_{9}$, 又数列 $\left\{a_{n}\right\}$ 的公差为 $-2, \therefore\left(a_{1}-12\right)^{2}=\left(a_{1}-4\right)\left(a_{1}-16\right)$, 解得 $a_{1}=20$, $\therefore a_{n}=20+(n-1) \times(-2)=22-2 n$, $\therefore S_{10}=\frac{10\left(a_{1}+a_{10}\right)}{2}=5 \times(20+2)=110$, 故选 D。

18924

[]

D

null

高二

在等差数列 $\left\{a_{n}\right\}$ 中, $a_{3}, a_{9}$ 是方程 $x^{2}+24 x+12=0$ 的两根, 则数列 $\left\{a_{n}\right\}$ 的前 11 项和等于 ( )

A. 66 B. 132 C. -66 D. -32

算术

因为 $a_{3}, a_{9}$ 是方程 $x^{2}+24 x+12=0$ 的两根, 所以 $a_{3}+a_{9}=-24$, 又 $a_{3}+a_{9}=-24=2 a_{6}$, 所以 $a_{6}=-12, S_{11}=\frac{11 \times\left(a_{1}+a_{11}\right)}{2}=\frac{11 \times 2 a_{6}}{2}=-132$, 故选 D.

18928

[]

D

null

高二

在明代程大位所著的《算法统宗》中有这样一首歌谣, “放牧人粗心大意, 三畜偷偷吃苗青, 苗主扣住牛马羊, 要求赔偿五斗粮, 三畜户主愿赔偿, 牛马羊吃得异样. 马吃了牛的一半, 羊吃了马的一半. ”请问各畜赔多少? 它的大意是放牧人放牧时粗心大意, 牛、马、羊偷吃青苗, 青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食 ( 1 斗 $=10$ 升), 三畜的主人同意赔偿, 但牛、马、羊吃的青苗量各不相同. 马吃的青苗是牛的一半, 羊吃的青苗是马的一半. 问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食?

A. $\frac{25}{7}, \frac{50}{7}, \frac{100}{7}$ B. $\frac{25}{14}, \frac{25}{7}, \frac{50}{7}$ C. $\frac{100}{7}, \frac{200}{7}, \frac{400}{7}$ D. $\frac{50}{7}, \frac{100}{7}, \frac{200}{7}$

算术

设羊户赔粮 $a_{1}$ 升,马户赔粮 $a_{2}$ 升,牛户赔粮 $a_{3}$ 升,则 $a_{1}, a_{2}, a_{3}$ 成等比数列,且公比 $q=2, a_{1}+a_{2}+a_{3}=50$, 则 $a_{1}\left(1+q+q^{2}\right)=50$, 故 $a_{1}=\frac{50}{1+2+2^{2}}=\frac{50}{7}, a_{2}=2 a_{1}=\frac{100}{7}, a_{3}=2^{2} a_{1}=\frac{200}{7}$, 故选 D

18930

[]

A

null

高二

数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和记为 $S_{n}, a_{n+1}=a_{n}-a_{n-1}\left(n \in \mathbf{N}^{*}, n \geq 2\right), a_{1}=2018, a_{2}=2017$, 则 $S_{100}=$

A. 2016 B. 2017 C. 2018 D. 2019

算术

因为 $a_{1}=2018, a_{2}=2017, a_{n+1}=a_{n}-a_{n-1}\left(n \in \mathrm{N}^{*}, n \geq 2\right)$, 所以 $a_{3}=-1, a_{4}=-2018$, $a_{5}=-2017, a_{6}=1, a_{7}=2018, \cdots$, 所以数列 $\left\{a_{n}\right\}$ 是周期数列, 周期为 6 , 因为 $a_{1}+a_{2}+\cdots+a_{5}+a_{6}=0$, 所以 $S_{100}=16\left(a_{1}+a_{2}+\cdots+a_{5}+a_{6}\right)+$ $a_{97}+a_{98}+a_{99}+a_{100}=a_{1}+a_{2}+a_{3}+a_{4}=2016$. 故选 $\mathrm{A}$.

18931

[]

D

null

高二

已知等比数列 $\left\{a_{n}\right\}$ 中, $a_{1}=1, a_{4}=\frac{1}{8}$, 且 $a_{1} a_{2}+a_{2} a_{3}+\cdots+a_{n} a_{n+1}<k$, 则 $k$ 的取值范围是

A. $\left[\frac{1}{2}, \frac{2}{3}\right]$ B. $\left[\frac{1}{2},+\infty\right)$ C. $\left[\frac{1}{2}, \frac{2}{3}\right)$ D. $\left[\frac{2}{3},+\infty\right)$

算术

设等比数列 $\left\{a_{n}\right\}$ 的公比为 $q$, 则 $q^{3}=\frac{a_{4}}{a_{1}}=\frac{1}{8}$, 解得 $q=\frac{1}{2}$, 所以 $a_{n}=\frac{1}{2^{n-1}}$, 所以 $a_{n} a_{n+1}=\frac{1}{2^{n-1}} \times \frac{1}{2^{n}}=\frac{1}{2^{2 n-1}}$, 所以数列 $\left\{a_{n} a_{n+1}\right\}$ 是首项为 $\frac{1}{2}$, 公比为 $\frac{1}{4}$ 的等比数列, 所以 $a_{1} a_{2}+a_{2} a_{3}+\cdots+a_{n} a_{n+1}=\frac{\frac{1}{2}\left(1-\frac{1}{4^{n}}\right)}{1-\frac{1}{4}}=\frac{2}{3}\left(1-\frac{1}{4^{n}}\right)<\frac{2}{3}$, 所以 $k \geq \frac{2}{3}$. 故 $k$ 的取值范围是 $\left[\frac{2}{3},+\infty\right)$. 故选 D.

18939

[]

A

null

高二

【2019 年高考全国 I 卷理数】记 $S_{n}$ 为等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和. 已知 $S_{4}=0, a_{5}=5$, 则 ( )

A. $a_{n}=2 n-5$ B. $a_{n}=3 n-10$ C. $S_{n}=2 n^{2}-8 n$ D. $S_{n}=\frac{1}{2} n^{2}-2 n$

算术

由题知, $\left\{\begin{array}{l}S_{4}=4 a_{1}+\frac{d}{2} \times 4 \times 3=0 \\ a_{5}=a_{1}+4 d=5\end{array}\right.$, 解得 $\left\{\begin{array}{l}a_{1}=-3 \\ d=2\end{array}, \therefore a_{n}=2 n-5, S_{n}=n^{2}-4 n\right.$, 故选 A.

18943

[]

C

null

高二

【2019 年高考全国 III 卷理数】已知各项均为正数的等比数列 $\left\{a_{n}\right\}$ 的前 4 项和为 15 , 且 $$ a_{5}=3 a_{3}+4 a_{1} $$ 则 $a_{3}=(\quad)$

A. 16 B. 8 C. 4 D. 2

算术

设正数的等比数列 $\left\{a_{n}\right\}$ 的公比为 $q$, 则 $\left\{\begin{array}{l}a_{1}+a_{1} q+a_{1} q^{2}+a_{1} q^{3}=15 \\ a_{1} q^{4}=3 a_{1} q^{2}+4 a_{1}\end{array}\right.$,解得 $\left\{\begin{array}{l}a_{1}=1, \\ q=2\end{array}, \therefore a_{3}=a_{1} q^{2}=4\right.$, 故选 C.

18944

[]

C

null

高二

若 $a>b$, 则（）

A. $\ln (a-b)>0$ B. $3^{a}<3^{b}$ C. $a^{3}-b^{3}>0$ D. $|a|>|b|$

算术

取 $a=2, b=1$, 满足 $a>b, \ln (a-b)=0$, 知 $\mathrm{A}$ 错, 排除 $\mathrm{A}$; 因为 $9=3^{a}>3^{b}=3$, 知 $\mathrm{B}$错, 排除 $\mathrm{B}$; 取 $a=1, b=-2$, 满足 $a>b, 1=|a|<|b|=2$, 知 $\mathrm{D}$ 错, 排除 $\mathrm{D}$, 因为幂函数 $y=x^{3}$ 是增函数, $a>b$, 所以 $a^{3}>b^{3}$, 故选 C.

18948

[]

A

null

高二

已知等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}, a_{2}=2, S_{7}=28$, 则数列 $\left\{\frac{1}{a_{n} a_{n+1}}\right\}$ 的前 2020 项和为 ( )

A. $\frac{2020}{2021}$ B. $\frac{2018}{2020}$ C. $\frac{2018}{2019}$ D. $\frac{2021}{2020}$

算术

因为数列 $\left\{a_{n}\right\}$ 是等差数列, 所以 $S_{7}=\frac{7\left(a_{1}+a_{7}\right)}{2}=7 a_{4}$. 设公差为 $d$, 因为 $a_{2}=2, S_{7}=28$, 所以 $\left\{\begin{array}{l}a_{1}+d=2, \\ 7\left(a_{1}+3 d\right)=28,\end{array}\right.$ 解方程组得 $\left\{\begin{array}{l}a_{1}=1, \\ d=1,\end{array}\right.$ 所以数列 $\left\{a_{n}\right\}$ 的通项公式为 $a_{n}=1+(n-1) \times 1=n$, 所以 $\frac{1}{a_{n} a_{n+1}}=\frac{1}{n \times(n+1)}$. 设 $T_{n}$ 为数列 $\left\{\frac{1}{a_{n} a_{n+1}}\right\}$ 的前 $n$ 项和, 则 $T_{n}=\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}+\ldots+\frac{1}{(n-1) \times n}+\frac{1}{n \times(n+1)}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}+\ldots+\frac{1}{n}-\frac{1}{n+1}$ $\therefore T_{2020}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{2020-1}-\frac{1}{2020}+\frac{1}{2020}-\frac{1}{2020+1}=1-\frac{1}{2021}=\frac{2020}{2021}$, 故选 A。

19166

[]

A

null

高二

（2011 安徽）若数列 $\left\{a_{n}\right\}$ 的通项公式是 $a_{n}=(-1) \cdot(3 n-2)$, 则 $a_{1}+a_{2}+\cdots+a_{10}=(\quad)$

A. 15 B. 12 C. -12 D. -15

算术

法一：分别求出前 10 项相加即可得出结论; 法二: $a_{1}+a_{2}=a_{3}+a_{4}=\cdots=a_{9}+a_{10}=3$, 故 $a_{1}+a_{2}+\cdots+a_{10}=3 \times 5=15$. 故选 A.

19167

[]

A

null

高二

设 $a, b \in \mathbf{R}$, 数列 $\left\{a_{n}\right\}$ 满足 $a_{1}=a, a_{n+1}=a_{n}^{2}+b, n \in \mathbf{N}^{*}$, 则 ( )

A. 当 $b=\frac{1}{2}, a_{10}>10$ B. 当 $b=\frac{1}{4}, a_{10}>10$ C. 当 $b=-2, a_{10}>10$ D. 当 $b=-4, a_{10}>10$

算术

(1)当 $b=0$ 时, 取 $a=0$, 则 $a_{n}=0, n \in \mathbf{N}^{*}$. (2)当 $b<0$ 时, 令 $x=x^{2}+b$, 即 $x^{2}-x+b=0$. 则该方程 $\Delta=1-4 b>0$, 即必存在 $x_{0}$, 使得 $x_{0}^{2}-x_{0}+b=0$, 则一定存在 $a_{1}=a=x_{0}$, 使得 $a_{n+1}=a_{n}^{2}+b=a_{n}$ 对任意 $n \in \mathbf{N}^{*}$ 成立, 解方程 $a^{2}-a+b=0$, 得 $a=\frac{1 \pm \sqrt{1-4 b}}{2}$, 当 $\frac{1+\sqrt{1-4 b}}{2} \leq 10$ 时, 即 $b \geqslant-90$ 时, 总存在 $a=\frac{1+\sqrt{1-4 b}}{2}$, 使得 $a_{1}=a_{2}=\ldots=a_{10} \leq 10$, 故 C、 $\mathrm{D}$ 两项均不正确. (3)当 $b>0$ 时, $a_{2}=a_{1}^{2}+b \geq b$, 则 $a_{3}=a_{2}^{2}+b \geq b^{2}+b$, $a_{4}=a_{3}^{2}+b \geqslant\left(b^{2}+b\right)^{2}+b$. (i) 当 $b=\frac{1}{2}$ 时, $a_{4} \geq\left[\left(\frac{1}{2}\right)^{2}+\frac{1}{2}\right]^{2}+\frac{1}{2}=\frac{17}{16}>1, a_{5}>1+\frac{1}{2}$, 则 $a_{6}>\left(1+\frac{1}{2}\right)^{2}+\frac{1}{2}=\frac{11}{4}>2$, $a_{7}>2^{2}+\frac{1}{2}=\frac{9}{2}$, $a_{8}>\left(\frac{9}{2}\right)^{2}+\frac{1}{2}=\frac{83}{4}>10$, 则 $a_{9}=a_{8}^{2}+\frac{1}{2}>10$, $a_{10}=a_{9}^{2}+\frac{1}{2}>10$, 故 A 项正确. (ii) 当 $b=\frac{1}{4}$ 时, 令 $a_{1}=a=0$, 则 $a_{2}=\frac{1}{4}, a_{3}=\left(\frac{1}{4}\right)^{2}+\frac{1}{4}<\frac{1}{2}$, 所以 $a_{4}=a_{3}^{2}+\frac{1}{4}<\left(\frac{1}{2}\right)^{2}+\frac{1}{4}=\frac{1}{2}$, 以此类推, 所以 $a_{10}=a_{9}^{2}+\frac{1}{4}<\left(\frac{1}{2}\right)^{2}+\frac{1}{4}=\frac{1}{2}$, 故 B 项不正确. 故本题正确答案为 A. 【名师点睛】遇到此类问题, 不少考生会一筹莫展. 利用函数方程思想, 通过研究函数的不动点, 进一步讨论 $\boldsymbol{a}$ 的可能取值, 利用“排除法”求解.

19180

[]

C

null

高二

等差数列 $\left\{a_{n}\right\}$ 满足 $a_{1}=2, a_{n+2}-a_{n}=3$, 则 $a_{2}=(\quad)$

A. 5 B. $\frac{5}{2}$ c. $\frac{7}{2}$ D. $\frac{3}{2}$

算术

由题意可知等差数列的公差为 $\frac{3}{2}$, 所以 $a_{2}=a_{1}+d=\frac{7}{2}$, 选 C.

19181

[]

A

null

高二

在数列 中, 若 $a_{1}=1, a_{2}=\frac{1}{2}$, $\frac{2}{a_{n+1}}=\frac{1}{a_{n}}+\frac{1}{a_{n+2}}\left(n \in N^{*}\right)$, 则该数列的通项为( ).

A. $a_{n}=\frac{1}{n}$ B. $a_{n}=\frac{2}{n+1}$ C. $a_{n}=\frac{2}{n+2}$ D. $a_{n}=\frac{3}{n}$

算术

$\because \frac{2}{a_{n+1}}=\frac{1}{a_{n}}+\frac{1}{a_{n+2}}\left(n \in N^{*}\right), \therefore$ 数列 $\left\{\frac{1}{a_{n}}\right\}$ 是等差数列,又 $\frac{1}{a_{2}}-\frac{1}{a_{1}}=2-1=1, \therefore \frac{1}{a_{n}}=1+(n-1)=n, \quad \therefore a_{n}=\frac{1}{n}$. 故选 A.

19188

[]

B

null

高二

(2014 重庆) 在等差数列 $\left\{a_{n}\right\}$ 中, $a_{1}=2, a_{3}+a_{5}=10$, 则 $a_{7}=(\quad)$

A. 5 B. 8 C. 10 D. 14

算术

由等差数列的性质得 $a_{1}+a_{7}=a_{3}+a_{5}$, 因为 $a_{1}=2, a_{3}+a_{5}=10$, 所以 $a_{7}=8$, 选 B.

19189

[]

B

null

高二

(2012 福建) 等差数列 $\left\{a_{n}\right\}$ 中, $a_{1}+a_{5}=10, a_{4}=7$, 则数列 $\left\{a_{n}\right\}$ 的公差为 ( )

A. 1 B. 2 C. 3 D. 4

算术

由题意有 $a_{1}+a_{5}=2 a_{3}=10, a_{3}=5$, 又 $\because a_{4}=7, \therefore a_{4}-a_{3}=2, \therefore d=2$.

19190

[]

A

null

高二

（2011 安徽）若数列 $\left\{a_{n}\right\}$ 的通项公式是 $a_{n}=(-1)^{n}(3 n-2)$, 则 $a_{1}+a_{2}+\cdots+a_{10}=(\quad)$

A. 15 B. 12 C. -12 D. -15

算术

$a_{1}+a_{2}+\cdots+a_{10}=-1+4-7+10+\cdots+(-1)^{10} \cdot(3 \times 10-2)$ $=(-1+4)+(-7+10)+\cdots+\left[(-1)^{9} \cdot(3 \times 9-2)+(-1)^{10} \cdot(3 \times 10-2)\right]=15$

19191

[]

D

null

高二

在等差数列 $\left\{a_{n}\right\}$ 中, $a_{3}+a_{4}=12$, 公差 $d=2$, 则 $a_{9}=(\quad)$

A. 14 B. 15 C. 16 D. 17

算术

$: \mathrm{a}_{3}+\mathrm{a}_{4}=12,: 2 \mathrm{a}_{1}+5 \mathrm{~d}=2 \mathrm{a}_{1}+10=12,: \mathrm{a}_{1}=1, \times \mathrm{a}_{9}=1+8 \mathrm{~d}=17$. 本题选择 D 选项.

19197

[]

D

null

高二

数列 $\left\{a_{n}\right\}$ 是等差数列, $a_{1}=1, a_{4}=8$, 则 $a_{5}=$

16 B. -16 C. 32 D. $\frac{31}{3}$

算术

因为 $a_{4}=8$, 所以 $a_{1}+3 d=8$, 又因为 $a_{1}=1$, 所以 $d=\frac{7}{3}$, 可得 $a_{5}=a_{1}+4 d=\frac{31}{3}$, 故选 D.

19198

[]

D

null

高二

数列 $\left\{a_{n}\right\}$ 是等差数列, $a_{1}=1, a_{4}=8$, 则 $a_{5}=(\quad)$

A. 16 B. -16 C. 32 D. $\frac{31}{3}$

算术

因为 $a_{4}=8$, 所以 $a_{1}+3 d=8$, 又因为 $a_{1}=1$, 所以 $d=\frac{7}{3}$, 可得 $a_{5}=a_{1}+4 d=\frac{31}{3}$, 故选 D.

19199

[]

D

null

高二

下面是关于公差 $d>0$ 的等差数列 $\left\{a_{n}\right\}$ 的四个命题: $p_{1}$ : 数列 $\left\{a_{n}\right\}$ 是递增数列; $\quad p_{2}$ : 数列 $\left\{n a_{n}\right\}$ 是递增数列; $p_{3}$ :数列 $\left\{\frac{a_{n}}{n}\right\}$ 是递增数列; $\quad p_{4}$ : 数列 $\left\{a_{n}+3 n d\right\}$ 是递增数列; 其中的真命题为

A. $p_{1}, p_{2}$ B. $p_{3}, p_{4}$ c. $p_{2}, p_{3}$ D. $p_{1}, p_{4}$

算术

设 $a_{n}=a_{1}+(n-1) d=d n+m$, 所以 $p_{1}$ 正确; 如果 $a_{n}=3 n-12$ 则满足已知, 但 $$ n a_{n}=3 n^{2}-12 n $$ 并非递增所以 $p_{2}$ 错; 如果若 $a_{n}=n+1$, 则满足已知, 但 $\frac{a_{n}}{n}=1+\frac{1}{n}$, 是递减数列, 所以 $p_{3}$ 错; $a_{n}+3 n d=4 d n+m$, 所以是递增数列, $p_{4}$ 正确.

19202

[]

C

null

高二

已知数列 $\left\{a_{n}\right\}$ 为等差数列, 且 $a_{2}=1$, 则 $2\left|a_{9}\right|+\left|a_{10}\right|$ 的最小值为 ( )

A. 3 B. 2 C. 1 D. 0

算术

设数列 $\left\{a_{n}\right\}$ 的公差为 $d, \because a_{2}=1, \therefore 2\left|a_{9}\right|+\left|a_{10}\right|=2|1+d|+|1+2 d|=\left\{\begin{array}{l}-3-4 d, d<-1 \\ 1,-1 \leq d \leq-\frac{1}{2} \\ 3+4 d, d>-\frac{1}{2}\end{array}\right.$,由分段函数的性质可得 $2\left|a_{9}\right|+\left|a_{10}\right|$ 的最小值为 1 , 故选 C.

19203

[]

A

null

高二

设 $S_{n}$ 等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和, 若 $a_{1}+a_{3}+a_{5}=3$, 则 $S_{5}=(\quad)$

A. 5 B. 7 C. 9 D. 11

算术

$a_{1}+a_{3}+a_{5}=3 a_{3}=3, a_{3}=1, S_{5}=\frac{5}{2}\left(a_{1}+a_{5}\right)=\frac{5}{2} \times 2 a_{3}=5 a_{3}=5$, 选 $\mathrm{A}$.

19204

[]

D

null

高二

（2019$\cdot$河南高考模拟 (理) ) 已知等差数列 $\left\{a_{n}\right\}$ 满足 $a_{1}=32, a_{2}+a_{3}=40$, 则 $\left\{\left|a_{n}\right|\right\}$ 前 12 项之和为 ( )

A. -144 B. 80 C. 144 D. 304

算术

为 $a_{2}+a_{3}=2 a_{1}+3 d=64+3 d=40 \Rightarrow d=-8$, 所以 $a_{n}=40-8 n$. 所以 $\left|a_{n}\right|=|40-8 n|=\left\{\begin{array}{l}40-8 n, n \leqslant 5, \\ 8 n-40, n>6,\end{array}\right.$ 所以前 12 项之和为 $\frac{5 \times(32+0)}{2}+\frac{7 \times(8+56)}{2}=80+224=304$.

19205

[]

C

null

高二

【山西省 2019 届高三高考考前适应性训练 (三) 数学试题】已知数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}$, 满足 $a_{1}=-\frac{2}{3}, S_{n}+\frac{1}{S_{n}}+2=a_{n}(n \geq 2)$, 则下面选项为等差数列的是 $(\quad)$

A. $\left\{S_{n}+1\right\}$ B. $\left\{S_{n}-1\right\}$ C. $\left\{\frac{1}{S_{n}+1}\right\}$ D. $\left\{\frac{1}{S_{n}-1}\right\}$ #

算术

因为 $a_{n}=S_{n}-S_{n-1}(n \geq 2)$, 代入 $S_{n}+\frac{1}{S_{n}}+2=a_{n}(n \geq 2)$ 得 $S_{n}=-\frac{1}{S_{n-1}+2}(n \geq 2)$, 则 $S_{1}=-\frac{2}{3}, S_{2}=-\frac{3}{4}, S_{3}=-\frac{4}{5}$,故 $S_{1}+1=\frac{1}{3}, S_{2}+1=\frac{1}{4}, S_{3}+1=\frac{1}{5}$, 所以 $\left\{S_{n}+1\right\}$ 不是等差数列, 故 A 错误; 同理, $S_{1}-1=-\frac{5}{3}, S_{2}-1=-\frac{7}{4}, S_{3}-1=-\frac{9}{5}$, 所以 $\left\{S_{n}-1\right\}$ 不是等差数列, 故 B 错误; $\frac{1}{S_{1}-1}=-\frac{3}{5}, \frac{1}{S_{2}-1}=-\frac{4}{7}, \frac{1}{S_{3}-1}=-\frac{5}{9}$, 所以 $\left\{\frac{1}{S_{n}-1}\right\}$ 不是等差数列, 故 D 错误; $\frac{1}{S_{1}+1}=3, \frac{1}{S_{2}+1}=4, \frac{1}{S_{3}+1}=5$, 所以 $\left\{\frac{1}{S_{n}+1}\right\}$ 是等差数列, 故选 C. 【名师点睛】本题考查数列的递推关系, 利用 $a_{n}=S_{n}-S_{n-1}(n \geq 2)$ 来求解, 考查计算推理的能力,属中档题.求解时, 由 $a_{n}=S_{n}-S_{n-1}(n \geq 2)$, 结合题中条件, 可得 $S_{n}=-\frac{1}{S_{n-1}+2}(n \geq 2)$, 代入数据,对选项逐一判断即可.

19207

[]

C

null

高二

(2018- 浙江高考模拟) 在等差数列 $\left\{a_{n}\right\}$ 中, 若 $\frac{a_{0}}{a_{n}}<-1$, 且它的前 $n$ 项和 $S_{n}$ 有最小值, 则当 $S_{n}>0$时, $n$ 的最小值为 ( )

A. 14 B. 15 C. 16 D. 17

算术

$\because$ 数列 $\left\{a_{n}\right\}$ 是等差数列, 它的前 $n$ 项和 $S_{n}$ 有最小值 $\therefore$ 公差 $d>0$, 首项 $a_{1}<0,\left\{a_{n}\right\}$ 为递增数列 $\because \frac{a_{9}}{a_{3}}<-1$ $\therefore a_{8} \cdot a_{9}<0, a_{8}+a_{9}>0$ 由等差数列的性质知: $2 a_{2}=a_{1}+a_{15}<0, a_{2}+a_{9}=a_{1}+a_{16}>0$. $\because S_{n}=\frac{\left(a_{1}+a_{n}\right) n}{2}$ $\therefore$ 当 $S_{n}>0$ 时, $n$ 的最小值为 16 . 故选 C.

19211

[]

A

null

高二

记 $S_{n}$ 为等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和. 已知 $S_{4}=0, a_{5}=5$, 则 ( )

A. $a_{n}=2 n-5$ B. $a_{n}=3 n-10$ C. $S_{n}=2 n^{2}-8 n$ D. $S_{n}=\frac{1}{2} n^{2}-2 n$

算术

由题知, $\left\{\begin{array}{l}S_{4}=4 a_{1}+\frac{d}{2} \times 4 \times 3=0 \\ a_{5}=a_{1}+4 d=5\end{array}\right.$, 解得 $\left\{\begin{array}{l}a_{1}=-3 \\ d=2\end{array}, \therefore a_{n}=2 n-5, S_{n}=n^{2}-4 n\right.$.故选 A. 【名师点睛】本题主要考查等差数列通项公式与前 $n$ 项和公式, 渗透方程思想与数学计算等素养. 利用等差数列通项公式与前 $n$ 项公式即可列出关于首项与公差的方程, 解出首项与公差, 再适当计算即可做了判断.

19212

[]

B

null

高二

【2018 年高考全国 I卷理数】设 $S_{n}$ 为等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和, 若 $3 S_{3}=S_{2}+S_{4}, a_{1}=2$, 则 $a_{5}=$

A. -12 B. -10 C. 10 D. 12

算术

设等差数列的公差为 $d$, 根据题中的条件可得 $3\left(3 \times 2+\frac{3 \times 2}{2} \cdot d\right)=2 \times 2+d+4 \times 2+\frac{4 \times 3}{2} \cdot d$, 整理解得 $d=-3$, 所以 $a_{5}=a_{1}+4 d=2-12=-10$. 故选 B. 【名师点睛】该题考查的是有关等差数列的求和公式和通项公式的应用, 在解题的过程中, 需要利用题中的条件, 结合等差数列的求和公式, 得到公差 $d$ 的值, 之后利用等差数列的通项公式得到 $a_{5}$ 与 $a_{1}, d$ 的关系, 从而求得结果.

19213

[]

C

null

高二

【2017 年高考全国 I 卷理数】记 $S_{n}$ 为等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和. 若 $a_{4}+a_{5}=24, S_{6}=48$, 则 $\left\{a_{n}\right\}$的公差为 ( )

A. 1 B. 2 C. 4 D. 8

算术

设公差为 $d, a_{4}+a_{5}=a_{1}+3 d+a_{1}+4 d=2 a_{1}+7 d=24$ ， $S_{6}=6 a_{1}+\frac{6 \times 5}{2} d=6 a_{1}+15 d=48$, 联立 $\left\{\begin{array}{l}2 a_{1}+7 d=24 \\ 6 a_{1}+15 d=48\end{array}\right.$, 解得 $d=4$. 故选 C. 【秒杀解】因为 $S_{6}=\frac{6\left(a_{1}+a_{6}\right)}{2}=3\left(a_{3}+a_{4}\right)=48$, 即 $a_{3}+a_{4}=16$, 则 $\left(a_{4}+a_{5}\right)-\left(a_{3}+a_{4}\right)=24-16=8$, 即 $a_{5}-a_{3}=2 d=8$, 解得 $d=4$. 故选 C. 【名师点睛】求解等差数列基本量问题时, 要多多使用等差数列的性质, 如 $\left\{a_{n}\right\}$ 为等差数列, 若 $m+n=p+q$, 则 $a_{m}+a_{n}=a_{p}+a_{q}$.